
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Производящая функция.
Вопрос. Гипергеометрическое распределение. Вопрос. Равномерное распределение.
7 вопрос. Распределение Пирсона (χ2-распределение). На самостоятельное изучение 8 вопрос. Распределение Стьюдента (t распределение). (конспект представить на 9 вопрос. Распределение Фишера-Снедекора (F -распределение). практических занятиях) Литература по теме: Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями: Учебное пособие. – М.: ИКЦ «МарТ»; Ростов-н/Д: Издательский центр «МарТ», 2005. – 608 с. Глава 5. Дискретные случайные величины. – С. 118 – 150 Глава 6. Непрерывные случайные величины. – С. 151 – 176 Ответы и решения Глава 5. Дискретные случайные величины. – С. 359 – 400 Глава 6. Непрерывные случайные величины. – С. 401 – 427 Приложения. – С. 550 – 587 Теория статистики с основами теории вероятностей: Учебное пособие для вузов/ И.И. Елисееева, В.С. Князевский, Л.И. Ниворожкина, З.А. Морозова; Под ред. И.И. Елисеевой. – М.: ЮНИТИ-ДАНА, 2001. – 446 с. Глава 5. Законы распределения дискретных случайных величин. – С. 90 – 128 Глава 7. Законы распределения непрерывных случайных величин. – С. 139 – 179 Приложения. – С. 427 – 435 3. Ниворожкина Л.И., Морозова З.А. Теория вероятностей и математическая статистика в определениях, формулах и таблицах: справочное пособие. – Ростов-н/Д: Феникс, 2007. – 192с. Глава 4. Дискретные случайные величины. – С. 21 – 30 Глава 5. Непрерывные случайные величины. – С. 31 – 43 Приложения. – С. 127 – 171 Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 543 с. Глава 2. Повторные независимые испытания. – С. 67 – 85. Глава 4. Основные законы распределения. – С. 140 – 174. Приложения. Математико-статистические таблицы. – С. 526 – 534.
1 вопрос. Биномиальное распределение.
p, 0<p<1
СВ Х имеет биномиальное распределение с параметрами n и p, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями:
Следующая таблица показывает как, в соответствии с формулой Бернулли, получаются биномиальные вероятности для всех значений случайной величины.
Функция распределения F(x):
Математическое ожидание М(Х)=nр Дисперсия σ2=D(X)=npq Среднее квадратическое отклонение
Пример 1. Рассмотрим результаты проверки качества, проведённой компанией Nestle на линии по выпуску шоколадных батончиков «Mars». Известно, что из каждых двадцати батончиков один бракованный. Таким образом, 5% (1/20) продукции выбрасывается и не идёт в продажу. Полностью проверить всю произведённую партию не представляется возможным. Случайным образом из партии отобрали 4 батончика. Составить биномиальный закон распределения числа батончиков, не соответствующих стандарту, и построить его график. Найти числовые характеристики этого распределения. Записать функцию распределения числа бракованных батончиков и построить её график. Чему равна вероятность, что среди 4-х случайно отобранных батончиков окажется не более 2 бракованных? Решение. В качестве случайной величины Х здесь выступает число батончиков «Mars» в выборке, которые не соответствуют стандарту. Возможные значения СВ Х: 0, 1, 2, 3, 4. Вероятность того, что каждый из отобранных батончиков бракованный, постоянна и равна 0,05 (p = 1/20=0,05). Вероятность противоположного события, т.е. того, что изделие соответствует стандарту, также постоянна и составляет 0,95 (q = 1 - p = 1 – 0,05 = 0,95). Все 4 испытания – независимы, т.е. вероятность появления бракованного батончика не зависит от того, бракованными или стандартными будут другие батончики. Таким образом, СВ Х подчиняется биномиальному закону распределения вероятностей с параметрами n=4 и p=0,05. Итак, по условию задачи: n = 4; p = 0,05; q = 0,95; X = m-0, 1, 2, 3, 4. Рассчитаем вероятности того, что СВ примет каждое из своих возможных значений по формуле Бернулли. Расчет искомых вероятностей осуществляется по формуле Бернулли.
Получим ряд распределения числа бракованных шоколадных батончиков в выборке:
СВ можно задать графически многоугольником (полигоном) распределения (рис. 1).
Рисунок 1. Полигон распределения вероятностей. Найдем числовые характеристики данного биномиального распределения: М(Х), D(Х), Математическое ожидание определим 2-мя способами: - как М(Х) ДСВ
- как М(Х) ДСВ, распределённой по биномиальному закону
Итак, среди случайно выбранных 4-х шоколадных батончиков можно ожидать появление в среднем 0,2 бракованных (точнее, менее одного). Дисперсию определим: - как D(X) ДСВ
- как D(X) ДСВ, распределённой по биномиальному закону
Среднее квадратическое отклонение Запишем биномиальный закон распределения в форме функции распределения
Рассчитаем значения F(х):
Эти данные можно представить и в виде таблицы:
График функции распределения вероятностей дискретной случайной величины имеет ступенчатый вид (рис. 2).
Рисунок 2. Функция распределения вероятностей. Вероятность того, что среди 4-х случайно отобранных батончиков окажется не более 2 бракованных (т.е. «или ноль, или один, или два»), найдём по теореме сложения вероятностей несовместных событий: P(X£ 2) = P(X=0)+P(X=1)+P(X=2)= 0,8145 + 0,1715 + 0,0135 = 0,9995.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.182.179 (0.068 с.) |
 6 вопрос. Нормальное распределение.
6 вопрос. Нормальное распределение.
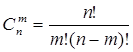 - число сочетаний
- число сочетаний



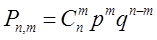


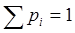


 .
.





 0,8145+0,1715+0,0135+0,0005+0=1
0,8145+0,1715+0,0135+0,0005+0=1
 .
.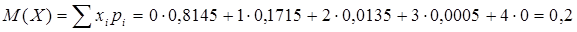 шт.
шт.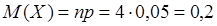 шт.
шт.

 шт.
шт.





