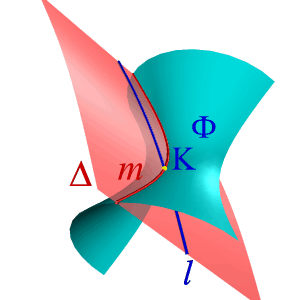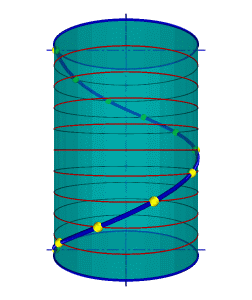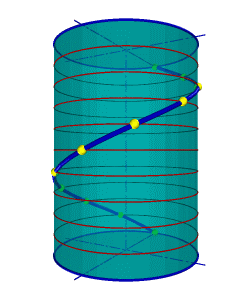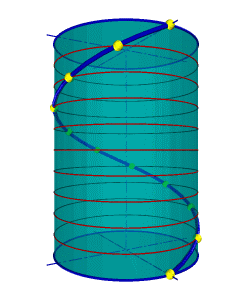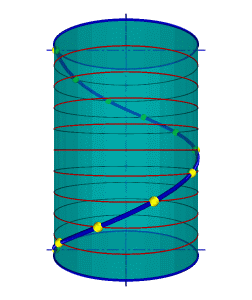
Цилиндрическая винтовая линия.

Такую линию в пространстве описывает точка, которая движется по какой-либо образующей прямого кругового цилиндра, вращающегося вокруг своей оси так, что путь проходимый точкой по образующей пропорционален углу поворота цилиндра (рис. 91).

 

а) модель	б) эпюр
Рисунок 91. Цилиндрическая винтовая линия (правая)

 

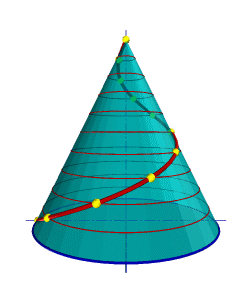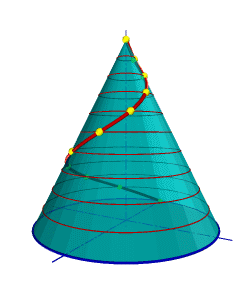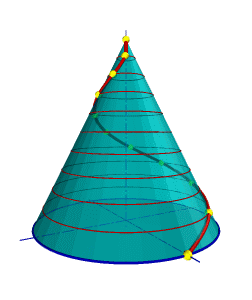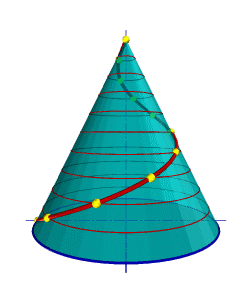
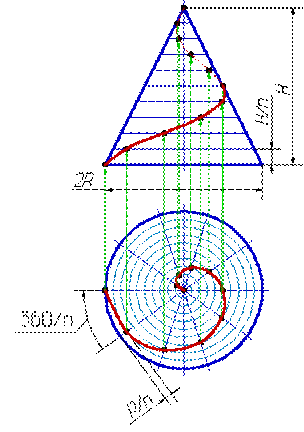
Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии. Различают правую и левую винтовые линии.

Коническая винтовая линия.

Такую линию описывает точка, которая движется по какой-либо образующей прямого кругового конуса, вращающегося вокруг своей оси так, что путь пройденный точкой по образующей все время равен углу поворота конуса (рис.92).

Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда - одна из замечательных плоских кривых линий.

 

а) модель	б) эпюр
Рисунок 92. Коническая винтовая линия

 

 

Поверхность Образование и задание поверхности на чертеже

 

Поверхность, одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.

1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых поверхности определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, поверхность шара - множество точек, отстоящих на заданном расстоянии от данной точки. Понятие "Поверхность" лишь поясняется, а не определяется. Например, говорят, что поверхность есть граница тела или след движущейся линии.

2) Математически строгое определение поверхности основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям)...."*

*Большая советская энциклопедия.

Поверхности составляют широкое многообразие объктов трехмерного пространства. Инженерная деятельность человека связана непосредственно с конструированием, расчетом и, изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации конструирования, расчета и воспроизведения сложных технических поверхностей. Способы формообразования и отображения поверхностей начертательной геометрии составляют основу инструментальной базы трехмерного моделирования современных графических редакторов.

Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z) - многочлен n -ой степени) и трансцендентные (F(x,y,z) - трансцендентная функция).

Если алгебраическая поверхность описывается уравнением n -й степени, то поверхность считается поверхностью n -го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

 

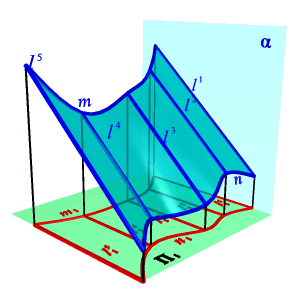
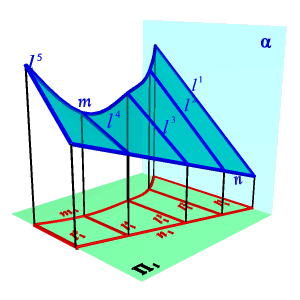
Поверхность можно рассматривать, как совокупность последовательных положений l ₁, l ₂… линии l перемещающейся в пространстве по определенному закону (рис.93). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму - изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в одной линии или целого семейства линий (m, n, p ...). Подвижную линию принято называть образующей, неподвижные - направляющими. Такой способ образования поверхности принято называть кинематическим.

 

Рисунок 93. Поверхность, образованная движением линии

 

Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.

По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.

Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.

Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Это так называемые циклические поверхности (рис.94).

 

Рисунок 94. Циклическая поверхность

 

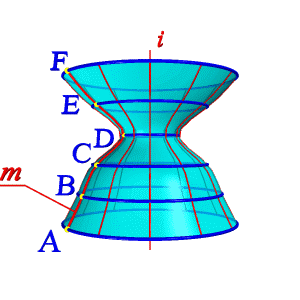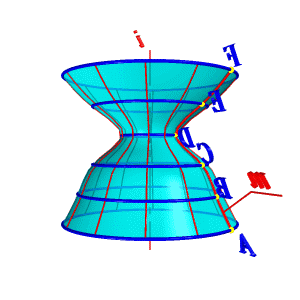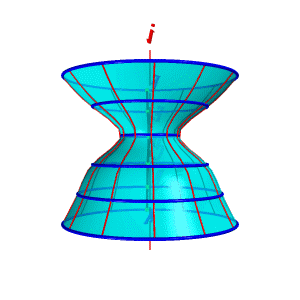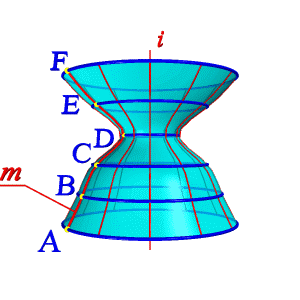
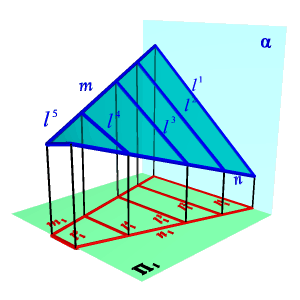
Если же группировать поверхности по закону движения образующей линии и производящей поверхности, то большинство встречающихся в технике поверхностей можно разделить на:

· поверхности вращения;

· винтовые поверхности;

· поверхности с плоскостью параллелизма;

· поверхности параллельного переноса.

Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают ее форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).

Для графического изображения поверхности на чертеже используется её каркас.

Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.

Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.

Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.

Различают две части определителя: геометрическую и алгоритмическую.

Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.

Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.

Например, циклическая поверхность, каркас которой состоит из окружностей (рис.95), может быть задан следующим образом:

·Геометрическая часть определителя: три направляющих l, m, n, ось i пучка плоскостей.

·Алгоритмическая часть: выделяем из пучка плоскостей с осью i плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим окружность, определяемую тремя найденными точками. Переходим к следующей плоскости пучка и повторяем построение.

 

Рисунок 95. Образование циклической поверхности

 

Поверхности вращения

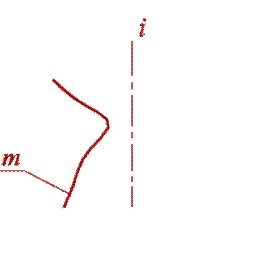
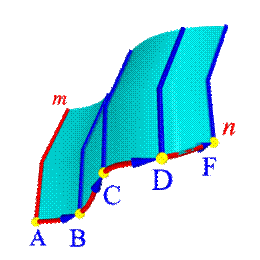
Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i (рис.96).

Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис 96.б).

Алгоритмическая часть включает две операции:

1. на образующей m выделяют ряд точек A, B, C,… F,

2. каждую точку вращают вокруг оси i.

а) модель	б) эпюр
Рисунок 96. Образование поверхности вращения

Так создается каркас поверхности, состоящей из множества окружностей (рис.97), плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором.

Из закона образования поверхности вращения вытекают два основных свойства:

1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.

2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум

симметричным относительно оси линиям – меридианам.

Плоскость, проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.

Рисунок 97. Поверхность вращения

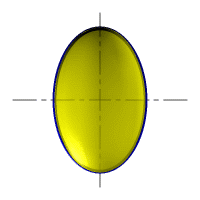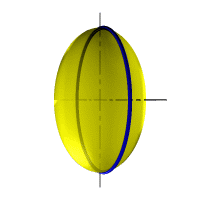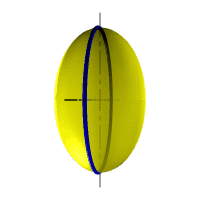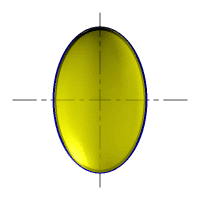
Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими:

Сфера – образуется вращением окружности вокруг её диаметра (рис.98).

При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг малой оси, то эллипсоид называется сжатым или сфероидом (рис.99), если вокруг большой – вытянутым (рис.100).

 

Рисунок 98. Образование сферы	Рисунок 99. Образование сфероида

Тор – образуется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.101).

Рисунок 100. Образование вытянутого эллипсоида	Рисунок 101. Тор

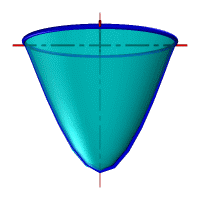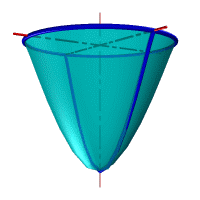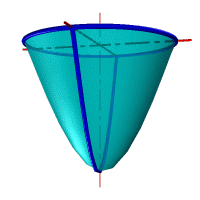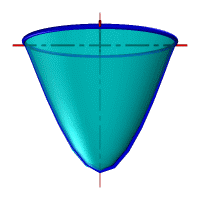
Параболоид вращения – образуется при вращении параболы вокруг своей оси (рис.102).

Рисунок 102. Параболоид вращения

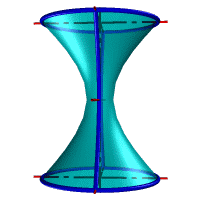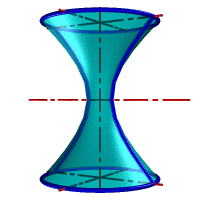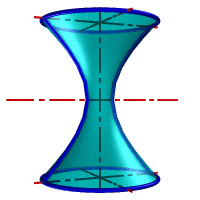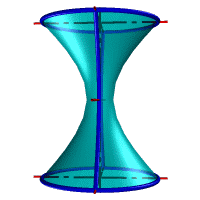
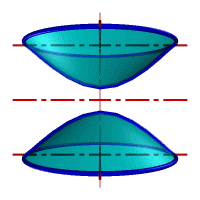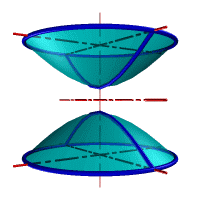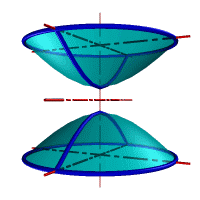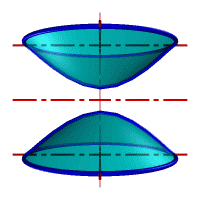
Гиперболоид вращения – различают одно (рис.103а) и двух (рис.103б) полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.

 

а) однополостной	б) двуполостной
Рисунок 103. Гиперболоид вращения

 

 

Винтовые поверхности

Винтовые поверхности образуются винтовым движением некоторой линии – образующей.

Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.

При этом поступательное и угловое перемещение находятся в определенной зависимости

∆h=k∆v,

где ∆h – линейное перемещение за время ∆t, ∆v – угловое перемещение за то же время, k – коэффициент пропорциональности. Если k=Const, то шаг поверхности постоянный.

Геометрическая часть определителя винтовой поверхности ничем не отличается от поверхности вращения и состоит из двух линий: образующей m и оси i (рис.104).

Алгоритмическая часть:

1. На образующей m выделяют ряд точек А, В, С, …

2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки.

Рисунок 104. Винтовая поверхность Поверхности с плоскостью параллелизма (поверхности каталана) Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n (рис. 105).       Рисунок 105. Цилиндроид В зависимости от формы направляющих образуются три частных вида поверхностей. Цилиндроид. Цилиндроидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим кривым линиям, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.105). Коноид. Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых кривая линия, а другая прямая, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.106).             Рисунок 106. Коноид Рисунок 107. Гиперболический параболоид Гиперболический параболоид. Гиперболическим параболоидом или косой плоскостью называется поверхность, образованная движением прямолинейной образующей, параллельной плоскости параллелизма, по двум направляющим линиям – скрещивающимся прямым (рис.107). поверхности параллельного переноса Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии m по криволинейной направляющей n (рис.108).         Рисунок 108. Поверхность параллельного переноса Геометрическая часть определителя состоит из двух кривых линий образующей - m и направляющей – n. Алгоритмическая часть определителя содержит перечень операций: 1. на направляющей п выбираем ряд точек А, В, С,… 2. строим векторы АВ, ВС,… 3. осуществляем параллельный перенос линии m по векторам АВ, ВС, … Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве. Взаимное расположение линии и поверхности Наиболее интересны два варианта взаимного расположения линии и поверхности: 1. Линия принадлежит поверхности - все точки линии принадлежат поверхности. 2. Линия пересекает поверхность - линия и поверхность имеют одну или несколько общих точек. Определение взаимного положения линии и поверхности - позиционная задача, для решения которой применяется метод вспомогательных секущих поверхностей посредников. При оценке взаимного расположения прямой линии и поверхности в качестве вспомогательных секущих поверхностей посредников используется плоскость - метод вспомогательных секущих плоскостей. Распространенными позиционными задачами в этой теме начертательной геометрии являются следующие: 1. Определение точек пересечения прямой линии и поверхности. 2. Построение прямой касательной поверхности. 3. Построение прямой перпендикулярной поверхности. Принадлежность линии поверхности Линия принадлежит поверхности, если все её точки принадлежат этой поверхности. В этой теме методами начертательной геометрии решаются следующие позиционные задачи: 1. Построение линии, принадлежащей поверхности. 2. Определение принадлежности линии поверхности. Рассмотрим алгоритм решения задачи на построение линии принадлежащей поверхности, если одна из проекций линии задана (рис.109). Дано: 1. Поверхность Ф, заданная проекциями каркаса состоящих из образующих линий l и направляющей n. 2. Фронтальная проекция линии m,принадлежащей поверхности Ф.         а) модель б) эпюр Рисунок 109. Линия на поверхности Алгоритм решения задачи: 1. Находим точки 12, 22, 32, 42 пересечения проекции линии m2 с проекцией каркаса поверхности, т.е. соответственно с проекциями линий l ^12, l ^22, l ^32, l ^42. 2. По линиям связи находим проекции точек 11, 21, 31, 41, как точки лежащие на проекциях образующих каркаса соответственно l ^11, l ^21, l ^31, l ^41 и определяющих положение проекции линии m1 на поверхности Ф. Пересечение линии с поверхностью Линия пересекает поверхность, если имеет с ней одну или несколько общих точек. Для графического определения точек пересечения линии с поверхностью (рис.110) необходимо выполнить ряд геометрических построений, описываемых следующим алгоритмом: 1. заключаем линию l в некоторую вспомогательную поверхность Δ; 2. строим линию m пересечения данной поверхности Ф и вспомогательной поверхности Δ; 3. определяем искомую точку К пересечения линии l и m (точка может быть не единственная). В качестве вспомогательной поверхности целесообразно использовать проецирующую цилиндрическую поверхность, направляющей которой должна служить заданная линия, а –прямолинейными образующими – проецирующие прямые.         Рисунок 110. Линия пересекает поверхность

При оценке взаимного расположения прямой линии и поверхности в качестве вспомогательных секущих поверхностей-посредников используется плоскость - метод вспомогательных секущих плоскостей.

Задача: Определить точки пересечения прямой линии с поверхностью конуса вращения и определить видимость прямой по отношению к конусу.

Для выбора вспомогательной секущей плоскости требуется знание линий образующихся в конических сечениях. Если в качестве вспомогательной секущей плоскости можно выбрать горизонтально проецирующую или фронтально проецирующую плоскости, то в сечении получатся соответственно гипербола (рис.111а) или эллипс (рис.111б). Построение кривых линий значительно усложняет задачу.

 

а) горизонтально проецирующая плоскость	б) фронтально проецирующая плоскость
Рисунок 111. Пересечение прямой линии с конусом (вспомогательная секущая плоскость - проецирующая)

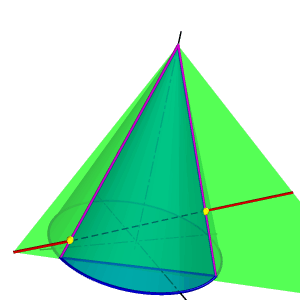
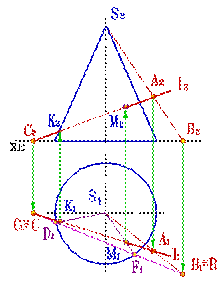
Поэтому в качестве вспомогательной секущей плоскости целесообразно выбрать такую плоскость, которая бы включала прямую l и пересекала конус по образующим (рис.112). Очевидно, что такая плоскость определяется прямой l и точкой S - вершиной конуса. Пусть основание конуса лежит в горизонтальной плоскости проекций, тогда линия пересечения вспомогательной секущей плоскости и горизонтальной плоскости проекций ВС пересекает основание конуса в точках D и F. Таким образом в сечении конуса вспомогательной секущей плоскостью получится треугольник DFS. Так как полученный треугольник и прямая l лежат в одной плоскости, точки их пересечения К и М и есть точки пересечения прямой с конусом.

	а) модель	б) эпюр
	Рисунок 112. Пересечение прямой линии с конусом (вспомогательная секущая плоскость-плоскость общего положения)
Принадлежность точки поверхности

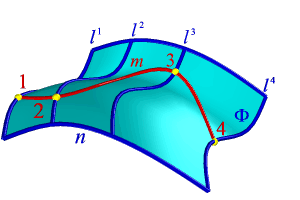
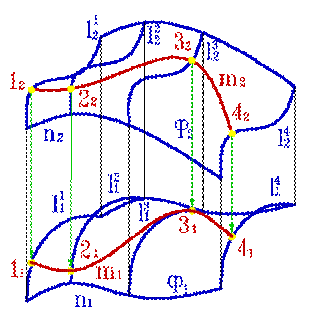
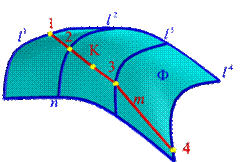
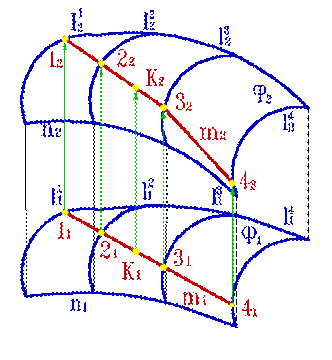
Точка может принадлежать поверхности или нет.

В этой теме решаются следующие позиционные задачи:

1. Построение точки, принадлежащей поверхности.

2. Определение принадлежности точки поверхности.

Рассмотрим алгоритм решения задачи на построение точки принадлежащей поверхности, если одна из проекций точки задана (рис.113).

Дано:

1. Поверхность Ф, заданная проекциями каркаса состоящего из образующих l и направляющих n.

2. Проекция точки К₁, принадлежащей поверхности Ф.

а) модель	б) эпюр
Рисунок 113. Точка на поверхности

Алгоритм решения задачи:

1. Через заданную проекцию точки К₁ проводим одноименную проекцию произвольной вспомогательной линии, принадлежащей поверхности m₁.

2. Находим точки 1₁, 2₁, 3₁, 4₁, пересечения проекции линии m₁ с проекцией каркаса поверхности, т.е. соответственно с проекциями линий l ¹₁, l ²₁, l ³₁, l ⁴₁.

3. По линиям связи находим проекции точек 1₂, 2₂, 3₂, 4₂ как точки, лежащие на проекциях образующих каркаса соответственно l ¹₂, l ²₂, l ³₂, l ⁴₂ и определяющих положение проекции линии m₂ на поверхности Ф.

4. По линии связи находим положение проекции точки К₂, как точку, принадлежащую вспомогательной линии m₂.

 

Взаимное расположение Плоскости и поверхности

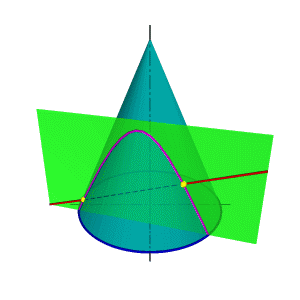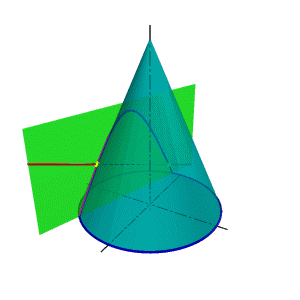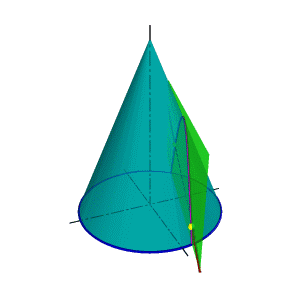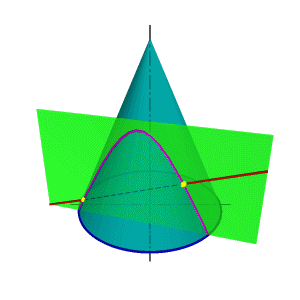
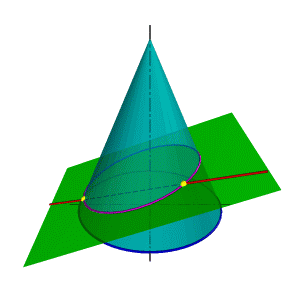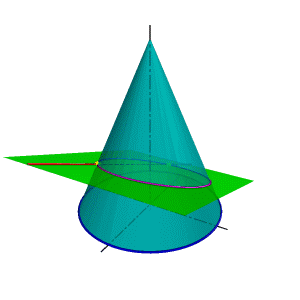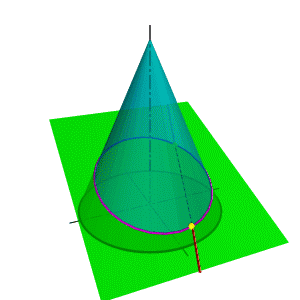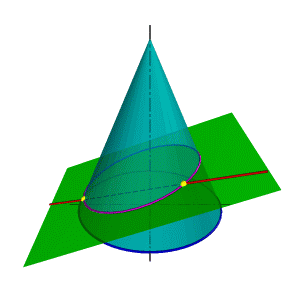
Рассмотрим два варианта взаимного расположения плоскости и поверхности:

1. Плоскость пересекает поверхность.

2. Плоскость касательная поверхности.

Определение взаимного положения плоскости и поверхности - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей используются проецирующиеся плоскости - плоскости перпендикулярные плоскостям проекций, поэтому основу метода вспомогательных секущих плоскостей составляет алгоритм решения задачи по нахождению линии пересечения поверхности проецирующей плоскостью.

Особое место занимают задачи по нахождению линии пересечения плоскости с конической поверхностью. В зависимости от положения секущей плоскости линией пересечения может быть окружность, эллипс, парабола, гипербола получивших название - линии конических сечений.

 

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ

В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая.