
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Добавление элемента (INSERT) ⇐ ПредыдущаяСтр 4 из 4
Дано: дерево Т и пара (K,V). Задача: добавить пару (K, V) в дерево Т. Алгоритм: § Если дерево пусто, заменить его на дерево с одним корневым узлом ((K,V), null, null) и остановиться. § Иначе сравнить K с ключом корневого узла X. § Если K>=X, рекурсивно добавить (K,V) в правое поддерево Т. § Если K<X, рекурсивно добавить (K,V) в левое поддерево Т. 63. Бинарное дерево поиска. Удаление элемента из бинарного дерева поиска. Удаление узла (REMOVE) Дано: дерево Т с корнем n и ключом K. Задача: удалить из дерева Т узел с ключом K (если такой есть). Алгоритм: § Если дерево T пусто, остановиться; § Иначе сравнить K с ключом X корневого узла n. § Если K>X, рекурсивно удалить K из правого поддерева Т; § Если K<X, рекурсивно удалить K из левого поддерева Т; § Если K=X, то необходимо рассмотреть три случая. § Если обоих детей нет, то удаляем текущий узел и обнуляем ссылку на него у родительского узла; § Если одного из детей нет, то значения полей ребёнка m ставим вместо соответствующих значений корневого узла, затирая его старые значения, и освобождаем память, занимаемую узлом m; § Если оба ребёнка присутствуют, то § найдём узел m, являющийся самым левым узлом правого поддерева с корневым узлом Right(n); § скопируем данные (кроме ссылок на дочерние элементы) из m в n; § рекурсивно удалим узел m. 64. Обход бинарного дерева Алгоритм обхода бинарного дерева посещает каждую вершину. При этом над каждой вершиной выполняется какая-либо операция, например, вывод содержания на экран или изменение данных. Для определённости будем считать, что при посещении вершины на экран просто выводятся записанные в неё данные. Рекурсивный алгоритм выглядит следующим образом.
traverse(BinaryTree binTree) { if(дерево binTree не пусто) { traverse(левое поддерево корня дерева binTree) traverse(правое поддерево корня дерева binTree) } }
Здесь не указаны инструкции, выполняющие вывод на экран данных, находящихся в корне. При обходе любого бинарного дерева алгоритм имеет три возможности посещения корня r. Он может посетить корень r перед обходом обоих поддеревьев, после обхода левого поддерева, но перед обходом правого, или после обхода обоих поддеревьев. Такой порядок называется прямым, симметричным и обратным, соответственно. 65. Балансировка бинарного дерева поиска
Алгоритмы вставки элемента в бинарное дерево поиска, поиска элемента по ключу, удаления элемента из бинарного дерева поиска требуют количества операций линейно зависящее от высоты дерева При вставке элементов в бинарное дерево поиска дерево может иметь как вид а) так и вид б).
а) б)
Очевидно, что в случае а) высота дерева равна числу узлов. Поэтому возникает задача приведения бинарного дерева поиска к виду с высотой как можно меньше.
Введём понятие уровня узла А.
Если узел А является корнем дерева Т, он принадлежит первому уровню. В противном случае уровень узла на единицу больше чем уровень его предка.
Бинарное дерево Т, имеющее высоту 1. все узлы, начиная с уровня 2. если узел, находящийся на уровне 3. если узел, находящийся на уровне
При симметричном обходе бинарного дерева поиска узлы посещаются в порядке возрастания ключа.
Если есть достаточное количество памяти, то можно воспользоваться следующим методом приведения бинарного дерева поиска к дереву с минимальной высотой. Записать все элементы из бинарного дерева поиска в массив при симметричном обходе, при этом массив будет упорядочен по возрастанию ключа. Удалить исходное дерево. Создать пустое бинарное дерево поиска. Вставлять элементы из массива длины
Insert_from_array(BinaryTree *binTree, Type_elem *a, int n) { if(n == 0) return; else{ Insert(binTree, a[n/2]); Insert_from_array(binTree, a, (n/2)); Insert_from_array(binTree, &a[n/2+1],(n-(n/2)-1)); } }
Здесь Insert(BinaryTree *binTree, Type_elem a) – функция вставляющая элемент в бинарное дерево поиска.
Для действительного числа
Доказательство по индукции. 1. При 2. Предположим, что оно верно при всех 3. Докажем для
Утверждение доказано.
В случае, когда нет возможности приводить дерево к дереву с минимальной высотой, приводят дерево к виду с высотой близкой к минимальной. Бинарное дерево поиска называется сбалансированным по высоте, или просто сбалансированным, если высота правого поддерева любого его узла отличается от высоты левого поддерева не больше чем на 1. Сбалансированное бинарное дерево поиска с Методы балансировки бинарных деревьев, требующие существенно меньших затрат памяти, чем изложенный, не рассматриваются в данном курсе.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.198.217 (0.008 с.) |
 .
. и выше, имеют по два дочерних узла;
и выше, имеют по два дочерних узла;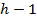 , имеет дочерние узлы, то все узлы, находящиеся на этом же уровне слева от него, имеют по два дочерних узла;
, имеет дочерние узлы, то все узлы, находящиеся на этом же уровне слева от него, имеют по два дочерних узла;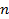 при помощи следующей рекурсивной функции (псевдокод).
при помощи следующей рекурсивной функции (псевдокод).






 обозначим
обозначим  – верхнюю грань, т.е. минимальное число не меньшее
– верхнюю грань, т.е. минимальное число не меньшее  его высоту. Докажем, что построенное таким образом бинарное дерево, с числом вершин
его высоту. Докажем, что построенное таким образом бинарное дерево, с числом вершин  , имеет высоту равную
, имеет высоту равную  .
. ,
,  утверждение верно.
утверждение верно. .
.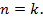 Высота полученного дерева равна
Высота полученного дерева равна  . Поскольку левое поддерево содержит не меньше вершин, чем правое, то
. Поскольку левое поддерево содержит не меньше вершин, чем правое, то
 и
и  (см. D. Knuth, The Art of Computer Programming, v.3).
(см. D. Knuth, The Art of Computer Programming, v.3).


