Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенный интеграл с переменным верхним пределом.
Определенный интеграл с переменным верхним пределом. Определенный интеграл с переменным верхним пределом является функцией от этого верхнего предела:
Теорема Барроу: производная от интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу, т.е.
Доказательство: возьмем любое значение х Î
Согласно свойству №2 определенных интегралов имеем
Отсюда находим приращение функции Ф(х):
Применим теперь интегральную теорему о среднем. Получим: Ф(х + Dх) – Ф(х) = f(c)Dx, где с – число, заключенное между х и х + Dх. Разделим обе части равенства на Dх:
Если теперь Dх ® 0, то с ® х, и тогда, в силу непрерывности функции f(x) на
Таким образом любая непрерывная на отрезке функция f(x) имеет на этом отрезке первообразные, причем функция Ф(х) – интеграл с переменным верхним пределом – является первообразной для f(x). А так как всякая другая первообразная для функции f(x) может отличаться от Ф(х) только на постоянную, то установлена связь между неопределенным и определенным интегралами в виде
Формула Ньютона-Лейбница. Таким образом, функция, непрерывная на отрезке
Пусть F(x) – любая другая первообразная для функции f(x) на том же отрезке
где С – некоторое число. Подставляем в эту формулу значение x = a, получаем
т.е. для любого х Î
Полагая x = b, получаем формулу Ньютона-Лейбница:
ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, специальная функция, определяемая интегралом
Этот интеграл не выражается в конечной форме через элементарные функции. Ecли х > 1, то интеграл понимается в смысле главного значения
И. л. введён в матем. анализ Л. Эйлером в 1768. И. л. Н(х) связан с интегральной показательной функцией Ei(x) соотношением li(х) = Ei(lnx). Для больших положительных х функция li(x) растёт как
ИНТЕГРАЛЬНЫЙ СИНУС И ИНТЕГРАЛЬНЫЙ КОСИНУС -специальные функции, определяемые соответственно интегралами
Эти функции введены итал. математиком Л. Маскерони в 1790. Однако ещё Л. Эйлеру (1781) было известно, что
Этот интеграл является простейшим примером сходящегося, но не абсолютно сходящегося несобственного интеграла. Функции Si(x) и Ci(x) встречаются в различных вопросах анализа и техники, и для них имеются подробные таблицы
Формула прямоугольников Если известны значения функции f(x) в некоторых точках x0, x1, …, xm, то в качестве функции “близкой” к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.
Если разбить отрезок интегрирования на n равных частей этом: y0 = f(x0), y1 = f(x1), …., yn = f(xn). Составим суммы: y0Dx + y1Dx + … + yn-1Dx y1Dx + y2Dx + … + ynDx Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной Тогда или любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников. Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников
Формула трапеций. Эта формула является более точной по сравнению с формулой прямоугольников. Подинтегральная функция в этом случае заменяется на вписанную ломаную.
y1 у2 уn
a x1 x2 b x
Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.
Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций:
Несобственные интегралы по неограниченному промежутку. Теорема сравнения. Пусть функция
Интегралы Эйлера. Гамма функция, свойства.
Г(p)= Область существования Г – функций. Непрерывность Г-функция сходящийся (по признаку Вейерштрасса) => равномерная сходимость по параметру, => подынтегральная функция непрерывна, => интеграл сходится к непрерывной функции, => Г-функция непрерывна
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.242.165 (0.014 с.) |


 и дадим ему приращение Dх ¹ 0 такое, чтобы Dх Î
и дадим ему приращение Dх ¹ 0 такое, чтобы Dх Î 



 , f(c) ® f(x). Поэтому, переходя к пределу при Dх ® 0, получаем:
, f(c) ® f(x). Поэтому, переходя к пределу при Dх ® 0, получаем:

 , имеет на этом отрезке первообразные, причем одной из них является функция
, имеет на этом отрезке первообразные, причем одной из них является функция











 . При
. При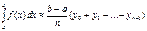

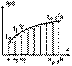




 интегрируема для всех
интегрируема для всех  и
и  . Если существует предел
. Если существует предел  , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его
, то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его  . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле
. Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле  . Аналогично определен интеграл
. Аналогично определен интеграл  для интегрируемой при
для интегрируемой при  функции
функции 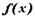 и интеграл
и интеграл  для функции, интегрируемой на
для функции, интегрируемой на  . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.
. Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.
 - сходящийся
- сходящийся – 1 род
– 1 род =>
=> 



 =>
=>