
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная и неопределенный интеграл. Свойства.Стр 1 из 4Следующая ⇒
Свойства определенного интеграла. Определенный интеграл. Обозначим через l длину наибольшего частичного отрезка Dxi данного разбиения. Определенным интегралом от функции f(x) по отрезку
Свойства определенного интеграла. 1. Из определения определенного интеграла следует а) если a = b, то
б) если поменять местами пределы, то определенный интеграл поменяет знак:
2. Какие бы ни были числа a, b, c, имеет место равенство:
Доказательство: допустим сначала, что a < b < c. Так как предел интегральной суммы s не зависит от способа разбиения отрезка
Переходя к пределу при l ® 0, получаем равенство *). Доказательства для других случаев расположения точек а, b, c легко сводятся к рассмотренному случаю с помощью первых двух свойств. 3. Постоянный множитель можно выносить за знак определенного интеграла. Доказательство: для любого разбиения отрезка
Переходя к пределу при l ® 0, имеем
4. Определенный интеграл от алгебраической суммы функций равен сумме их интегралов. Действительно, для любого разбиения отрезка
Замечание: свойство №4 имеет место для любого конечного числа слагаемых. 5. Если всюду на отрезке
Доказательство: в самом деле любая интегральная сумма для функции f(x) ³ 0 на отрезке
6. Если всюду на отрезке
Согласно свойству №5 для функции f(x) – g(x):
Но согласно свойству №4:
Таким образом, получаем неравенство
Определенный интеграл, его геометрический смысл. Определенный интеграл. Обозначим через l длину наибольшего частичного отрезка Dxi данного разбиения. Определенным интегралом от функции f(x) по отрезку
В случае, если такой предел существует, функция называется интегрируемой на
геометрический смысл определенного интеграла: если
теорема о среднем. Обобщенная теорема о среднем. Непрерывность Г-функция сходящийся (по признаку Вейерштрасса) => равномерная сходимость по параметру, => подынтегральная функция непрерывна, => интеграл сходится к непрерывной функции, => Г-функция непрерывна
Первообразная и неопределенный интеграл. Свойства. Первообразная. Первообразной функцией для данной функции f(x) на данном промежутке называется такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке. Любая функция имеет бесчисленное множество первообразных. Теорема: две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на постоянное слагаемое. Доказательство: пусть F¢1(x) = f(x) и F¢2(x) = f(x). Таким образом F¢1(x) = F¢2(x). Рассмотрим производную разности (F1(x) – F2(x))¢ = F¢1(x) - F¢2(x) = 0. Производная разности двух функций равна нулю, следовательно, эти функции отличаются друг от друга на константу, ч. т. д. Неопределенный интеграл. Неопределенным интегралом от функции f(x) называется общее выражение для всех первообразных данной непрерывной функции f(x) или от дифференциального выражения f(x)dx. Неопределенный интеграл обоначается
Интеграл является функцией общего вида, дифференциал которой равен подынтегральному выражению. Таким образом, можно записать:
Свойства неопределенного интеграла: 1. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции (следует из определения). 2. Неопределенный интеграл от дифференциала непрерывной дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого. 3. Отличный от нуля постоянный множитель можно выносить за знак интеграла:Aòf(x)dx = A(F(x)+C) = AF(x) + C1. 4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же алгебраической сумме интегралов этих функций:
òf(x)dx + òg(x)dx = (F(x) + C1) + (G(x) + C2) = (F(x) + G(x)) + C. 5. Неопределенный интеграл не зависит от выбора аргумента. Доказательство: положим u = j(x), где j(х) – некоторая непрерывно дифференцируемая функция. Рассмотрим интеграл: òf(u)du = òf(u)u¢dx. (1) В таком случае сложная функция F(u) = F(j(x)) является первообразной для подынтегральной функции интеграла (1). Действительно, в силу независимости дифференциала первого порядка от выбора переменной, получаем: dF(u) = F¢(u)du = f(u)du. И, следовательно,
Поэтому òf(u)du = F(u) + C, где А¢(г) = а(г)б ч. т. д. Интегрирование путем замены переменной. Пусть f(x) непрерывна на интервале (а,b) и x = j(t) непрерывно дифференцируема на интервале (a,b), причем функция j отображает интервал (a,b) в интервал (a,b). На основании свойства независимости неопределенного интеграла от выбора аргумента, и учитывая, что dx = j¢(t)dt, получаем формулу замены переменной в неопределенном интеграле: òf(x)dx = òf(j(t))j¢(t)dt. Интегрирование по частям. Пусть u и v – непрерывно дифференцируемые функции от x. На основании формулы дифференциала произведения имеем: d(uv) = udv + vdu; udv = d(uv) – v(du). Интегрируем последнее выражение. Получаем: òudv = òd(uv) - òvdu; òudv = uv - òvdu. Полученная формула называется формулой интегрирования по частям.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.97.157 (0.013 с.) |
 называется конечный предел I интегральной суммы s, если такой предел существует:
называется конечный предел I интегральной суммы s, если такой предел существует: В случае, если такой предел существует, функция называется интегрируемой на
В случае, если такой предел существует, функция называется интегрируемой на 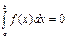 ;
;
 . *)
. *) .
. .
.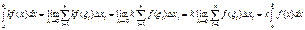 .
.

 .
. , получаем:
, получаем: .
. g(x), то
g(x), то .
. .
. .
.
 называется конечный предел I интегральной суммы s, если такой предел существует:
называется конечный предел I интегральной суммы s, если такой предел существует:
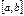 .
. , то
, то  равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми
равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми 


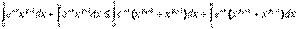
 .
. .
.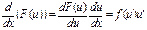 .
.


