
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная ф-и задана неявно ⇐ ПредыдущаяСтр 4 из 4
Функция z=f(x,y) наз. Заданной неявно, если она определена равенством, неразрешенным относительно z.F(x,y,z)=0 x+y+z=ez - это равенство задаем некоторую функцию z=f(x,y), которую нельзя выразить в полном виде.x2+y2+z2=0 - не задает никакой функции. Теорема: Если ф-я F(x,y,z) - непрерывна в т. р0(x0,y0,z0) и ее производная по z Fz(x,y,z)¹0, то равенство F(x,y,z)=0 однозначно определяет в неявном виде функцию z=f(x,y), при этом эта функция дифференцируема и ее производная находится по формулам: ¶z/¶x=- F¢x(x,y,z)/F¢z(x,y,z) ¶z/¶y=-F¢z (x,y,z)/F¢y(x,y,z) Док-во: Найдем полный дифференциал функции dF(x,y,z)=¶F/¶x*dx+¶F/¶y*dy+¶F/¶x*dz F(x0,y0,z0)=0èdF=0è¶F/¶x*dx+¶F/¶y*dy+¶F/¶x*dz=0 dz=-(¶F/¶x)/(¶F/¶z)*dx-(¶F/¶y)/(¶F/¶z)*dy (*) С другой стороны: z=f(x,y), dz=¶z/¶x*dx+¶z/¶y*dy (**) Сравнивая (*) и(**) è ¶z/¶x=- F¢x(x,y,z)/F¢z(x,y,z)¶z/¶y=-F¢z (x,y,z)/F¢y(x,y,z)
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла). Доказательство. Пусть х0 Î (a, b). Проведем касательную к кривой в этой точке.Уравнение кривой: y = f(x);Уравнение касательной:
Парабола и ее свойства. Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз. параболой.
y2=2px-симметрично отн. оси ОХ х2=2pу-симметрично отн. оси ОУ Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса. Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2 Св-ва: 1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2. 12.2.Эллипс и его св-ва: Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки Аx2+Cy2=d ур.-е наз. канонич. ур.-ем эллипса, где
Точки F1(-c,0) и F2(c,0) - наз. фокусами эллипса а. Отношение e=с/а наз. его эксцентриситетом (0<=e<=1) Точки A1,A2,B1,B2 -вершины эллипса. Св-во: Гипербола и ее св-ва. Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2+Cy2=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0 б) Если d>0, то каноническое ур-е гиперболы примет вид: x2/a2-y2/b2=1, F1(c,o) и F2(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет. Св-во: б) если d=0, ур-е примет вид x2/a2-y2/b2=0, получаем 2 перекрестные прямые х/а±у/b=0 в) если d<0, то x2/a2-y2/b2=-1 - ур-е сопряженной гиперболы.
15. 1. Скалярное произведение векторов: его свойства скаляр проивед векторов называется произведение их модулей на косинус угла между ними. Оно обозначается
Два вектора
Свойства скалярного произведения: 1. 2. 3. 4. Докажем распределительное свойство:
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.213.235 (0.01 с.) |
 20.4.Точки перегиба граф ф- ии.Пример Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
20.4.Точки перегиба граф ф- ии.Пример Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.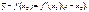 Следует доказать, что
Следует доказать, что  .По теореме Лагранжа для f(x) – f(x0):
.По теореме Лагранжа для f(x) – f(x0):  , x0 < c < x.
, x0 < c < x.  По теореме Лагранжа для
По теореме Лагранжа для 
 Пусть х > x0 тогда x0 < c1 < c < x. Т.к. x – x0 > 0 и c – x0 > 0, и кроме того по условию
Пусть х > x0 тогда x0 < c1 < c < x. Т.к. x – x0 > 0 и c – x0 > 0, и кроме того по условию  , следовательно,
, следовательно,  .Пусть x < x0 тогда x < c < c1 < x0 и x – x0 < 0, c – x0 < 0, т.к. по условию
.Пусть x < x0 тогда x < c < c1 < x0 и x – x0 < 0, c – x0 < 0, т.к. по условию  то
то  .Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).Теорема доказана. Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная пересекает кривую. Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба. Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.Теорема доказана.
.Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).Теорема доказана. Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная пересекает кривую. Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба. Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.Теорема доказана. Если вершина нах. в О(0,0), то ур-е примет вид
Если вершина нах. в О(0,0), то ур-е примет вид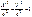

 При а=в представляет собой ур-е окружности х2+y2=а2
При а=в представляет собой ур-е окружности х2+y2=а2
 .
.  – есть проекция
– есть проекция  на
на  и
и  – проекция
– проекция 
 тогда и только тогда, когда
тогда и только тогда, когда  .
. – переместительное свойство;
– переместительное свойство;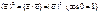 – скалярный квадрат вектора;
– скалярный квадрат вектора;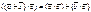 – распределительное свойство;
– распределительное свойство; – сочетательное свойство относительно числового множителя.
– сочетательное свойство относительно числового множителя.



