
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дробный факторный экспериментСтр 1 из 10Следующая ⇒
Не числом, а уменьем. Поговорка Количество опытов в полном факторном эксперименте значительно превосходит число определяемых коэффициентов линейной модели. Другими словами, полный факторный; эксперимент обладает большой избыточностью опытов. Было бы заманчивым сократить их число за счет той информации, которая не очень существенна при построении линейных моделей. При этом нужно стремиться к тому, чтобы матрица планирования не лишилась своих оптимальных свойств. Сделать это не так просто, но все же возможно. Итак начнем поиск путей минимизации числа опытов [1-3]. 7.1. Минимизация числа опытов Начнем с самого простого — полного факторного эксперимента 22. Напишем еще раз эту хорошо нам известную матрицу (табл. 7.1).
Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперимента в виде неполного квадратного уравнения У=b0+b1x1+Ь2х2+Ъпххх2. Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента; Ь0, Ъх и Ь2. Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении 612 СК и вектор-столбец хгх2 можно использовать для нового фактора х3. Поставим этот фактор в скобках над взаимодействием хгх2 и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые мы имели в полном факторном эксперименте 2к. Оценки смешаются следующим образом: Но нас это не должно огорчать. Ведь мы постулируем линейную модель, и, следовательно, все парные взаимодействия незначимы. Главное, мы нашли средство минимизировать число опытов: вместо восьми опытов для изучения трех факторов оказывается можно поставить четыре! При этом матрица планирования не теряет своих оптимальных свойств (ортогональность, ротатабель- ность и т. п.), в чем вы можете самостоятельно убедиться. Найденное правило можно сформулировать так: чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца.
Посмотрите, пожалуйства, на три матрицы, приведенные ниже. Эти матрицы предлагаются взамен полного факторного эксперимента 2s, требующего, как вы знаете, восьми опытов. Каким бы из них вы воспользовались?
Проверим свойства матрицы № 1. Каждый вектор-столбец матрицы, кроме первого, содержит^равное число +1 и —1. Это означает, что выполняется условие: #2(.;Г8{ = 4, т. е. совершена какая-то ошибка в выборе матрицы. Постараемся ее найти. Вектор-столбцы для хх и х2 не вызывают сомнения. Ведь эта часть матрицы — полный факторный эксперимент 2[6]. А как построен вектор-столбец для х3? Элементы этого столбца обратны по знаку элементам соседнего столбца хг. Два этих столбца оказались взаимосвязанными: х3 — —х2. При этом Ъ3 -> — (32 и &2 (32— (З3. В таком планировании не могут быть раздельно оценены основные эффекты. Значит, мы потеряли информацию о двух линейных коэффициентах нашей модели. Таким планированием воспользоваться невозможно. Матрица № 2 содержит всего три опыта. Три опыта недостаточны для оценки четырех коэффициентов: Ь0, blt b2 и b3. Кроме того, ни одно из свойств, присущих полному факторному эксперименту, здесь не выполняется, за исключением нормировки. Матрица № 3 сохраняет все свойства полного факторного эксперимента. Она дает возможность оценить свободный член Ь0 и три коэффициента при линейных членах, потому что для х3 использован вектор-столбец хгх2 полного факторного эксперимента 2®.
Если мы в дополнение к столбцам матрицы № 3 вычислим еще столбцы для произведений ххх3 и х2х3, то увидим, что элементы столбца ххх3 совпадут с элементами столбца х2, а элементы столбца х2х3 — с элементами столбца xv Найденные нами коэффициенты будут оценками для совместных эффектов W р!+ Рм, b2 р2+ р18; ь3 р3+ pJ2. Такое планирование нас вполне устраивает. Мы смешали эффекты взаимодействия с основными эффектами. (Но все основные эффекты оцениваются раздельно друг от друга!) Так как постулируется линейная модель, то предполагается, что эффекты взаимодействия близки к нулю, и поэтому Ьг ~ (3lt b2 ~ (32, Ь3 ~ Мы рассмотрели самый простой случай: матрицу из четырех опытов для трехфакторного планирования. С увеличением числа факторов вопрос о минимизации числа опытов превращается в довольно сложную задачу. Рассмотрим ее детально. При этом нам не обойтись без новых определений и понятий. 7.2. Дробная реплика Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной полного факторного эксперимента 2s, или «полурепликой». Если бы мы xs приравняли к —хххг, то получили бы вторую половину матрицы 2s. В этом случае: -> pj—|323; Ъг -> —j313, frg -> jB3—|312. При реализации обеих полуреплик можно получить раздельные оценки для линейных эффектов и эффектов взаимодействия, как и в полном факторном эксперименте 23. Объединение этих двух полуреплик и есть полный факторный - эксперимент 23. Матрица из восьми опытов для четырехфакторного планирования будет полурепликой от полного факторного эксперимента 24, а для пятифакторного планирования — четверть-репликой от 2В. В последнем случае два линейных эффекуа приравниваются к эффектам взаимодействия. Для обозначения дробных реплик, в которых р линейных эффектов приравнены к эффектам взаимодействия, удобно пользоваться условным обозначением 2к~р. Так, полуреплика от 2е запишется в виде 26~*, а четверть-реплика от 25 — в виде 2б~2.
Условные обозначения дробных реплик и количество опытов приведены в табл. 7.2. 7.3. Выбор полуреплик. Генерирующие соотношений и определяющие контрасты При построении полуреплики 2sсуществует всего две возможности: приравнять xs к -\-хгх2 или к —хгхг. Поэтому есть только две нолуреплики 23-1 (табл. 7.3).
Для произведения трех столбцов матрицы I выполняется соотношение: -\-1=х1хгх3, а матрицы II: —1 =x1x2xss. Вы видите, что все знаки столбцов произведений одинаковы и в первом случае равны плюс единице, а во втором — минус единице. Символическое обозначение произведения столбцов, равного +1 или —1, называется определяющим контрастом. Контраст помогает определять смешанные эффекты. Для того чтобы определить, какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту. Так, если 1=х1хгхй, то для х1 имеем /V* ------- At2 /Vt /V» ■-------- /V» (И — — ^31 так как всегда Для х2 находим ДЛЯ xs f --- f T t*2 —— <y> <y> U/g — 3 12 * Это значит, что коэффициенты линейного уравнения будут оценками P1+P2S» &S->-Ps+Pl2- Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генерирующим соотношением. Полуреплики, в которых основные эффекты смешаны с двух- факторными взаимодействиями, носят название планов с разрешающей способностью III (по наибольшему числу факторов в определяющем контрасте). Такие планы принято обозначать: 2М. При выборе полуреплики 24-1 возможно восемь решений: 1) х^ — ххх2, 4) х^ = х2х^, 7) хг = х1^х2х3, 2) Х^-------- XjХ>2, 5) Х^----- XjXg, 8) Х^----- Х-^Х.^Х^. 3) Хц = х2хъ, 6) xi=z=—x1xt, 7 Закав М 588 Разрешающая способность этих полуреплик различна. Так, реплики 1—6 имеют по три фактора в определяющем контрасте, а 7—8 но четыре. Реплики 7 и 8 имеют максимальную разрешающую способность и называются главными. Разрешающая способность задается системой смешивания данной реплики. Она будет максимальной, если линейные эффекты смешаны с эффектами взаимодействия наибольшего возможного порядка. При отсутствии априорной информации об эффектах взаимодействия экспериментатор стремится выбрать реплику с наибольшей разрешающей способностью, так как тройные взаимодействия обычно менее важны, чем парные. Если существует информация об эффектах взаимодействия, то она должна использоваться при выборе •реплики.
Реплики, в которых нет ни одного главного эффекта, смешанного с другим главным эффектом или парным взаимодействием, а все парные взаимодействия смешаны друг с другом, носят название планов с разрешающей способностью IV (по наибольшему числу факторов в определяющем контрасте). Они имеют обозначение 2fV. Полуреплика, заданная определяющим контрастом 1имеет только четные комбинации букв в каждой строке. Ее можно записать следующим образом, считая строку (1) четной: (1), ad, bd, ab, ас, cd, be, abed. А полуреплика, заданная 1 = —x1x2xsxi, имеет только нечетные комбинации а, Ь, с, d, abd, acd, abc, bed. Такие полуреплики называют главными полурепликами, так как они обладают наибольшей разрешающей способностью. Пусть выбраны полуреплики, заданные определяющими контрастами l=x1x2xsxl и 1 = — ххх2х^х^. Совместные оценки здесь определяются соотношениями:
X^OCg Х^Х^,
Х]Х^ = Х2Х%,
Такой тип смешивания даст возможность оценивать линейные эффекты совместно с эффектами взаимодействий второго порядка, а взаимодействия первого порядка — совместно друг с другом. Если полуреплики заданы генерирующими соотношениями х1=осхх% и #4=—Х]Х2, то в этом случае определяющими контрас- тами являются 1 =x±x2xt и l = —x1x2xi, следовательно, мы получаем планы с разрешающей способностью III и некоторые основные эффекты емешиваем с парными взаимодействиями: Х^--- х2х^,
Х2 — Х^Х ^у
Разрешающая способность этих полуреплик ниже, чем у планов с разрешающей способностью IV, с помощью которых линейные эффекты определяются независимо от парных взаимодействий. Эти полуреплики имеют в каждой строке как четные, так и нечетные комбинации букв. Такие полуреплики не являются главными. Разумен выбор такой полуреплики, если имеется априорная информация о большей значимости тройных взаимодействий по сравнению с парными или о незначимости трех парных взаимодействий x2xit xlxi, хгх2. Как видите, выбор дробной реплики требует много терпенья и труда. Но другого пути нет. Применяя дробное планирование, нужно точно знать систему смешивания, четко представлять, какую информацию приходится терять. - Теперь рассмотрим пример полуреплики 2|у. Пример 1. Этот пример относится к планированию эксперимента для отыскания оптимальных условий получения нового полимерного серусодер- жащего антиоксиданта, синтезированного превращением высокомолекулярного полистирола с серой [4]. Задача состояла в получении стабилизатора, введение которого в изотактический полипропилен увеличивало бы период индукции, не ухудшая физико-механических свойств полимера. В качестве факторов рассматривались переменные, показанные в табл. 7-4. Матрица планирования представляла собой полуреплику от 24, заданную генерирующим соотношением xi=xlx2x3. Определяющим контрастом является i=x1x2x3xi. Умножая определяющий контраст последовательно на xlt хг, х3 и х4, определяем совместно оценки линейных эффектов и взаимодействий
61Pi + Рг34> Рв-Н124. &12 -* Pl2 + Рв4. &2Р2 + Pl»4. &4-»P4 + Pl23. 613 Pl8 + Р24. 628 Pas + Pl4* Матрица планирования, результаты эксперимента и коэффициенты регрессии показаны в табл. 7.5. Анализ результатов и поиск оптимальных условий приводятся в последующих главах. 7* 99
Поговорим теперь о полуреплике 25-1. При выборе полуреплики 25-1 в распоряжении экспериментатора имеется множество вариантов. Так, хь можно приравнять к одному из шести парных взаимодействий. В этом случае получим полуреплику с разрешающей способностью III. Очевидно, это будет не лучший выбор полуреплики. Далее, хъ можно приравнять к одному нз четырех тройных взаимодействий. Тогда получим план с разрешающей способностью IV, и все линейные эффекты будут смешаны с тройными взаимодействиями. И, наконец, полу- реплика может быть задана генерирующими соотношениями Хс — Х^Х^Х^Х^ ИЛИ Jg— X ^X^XqX^. Определяющими контрастами в этом случае будут 1 =x1x2xexix& и l——x1xixazix5. Такие реплики носят название планов с разрешающей способностью V и обозначаются 2у\ Пусть имеется пять факторов и для них нужно выбрать полу- реплику с наибольшей разрешающей способностью. Для полуреплики, заданной генерирующим соотношением l=xlxaxix6, следовательно,
Смешивание основных эффектов с тройными взаимодействиями, когда существуют эффекты взаимодействия более высокого порядка, нельзя признать наилучшим, если нет специальных соображений. Если выбрана полуреплика, заданная генерирующим соотношением x!i=x1x2x3xi и, следовательно, определяющим контрастом l=x1x2x3xixs, то коэффициенты определяют такие смешанные оценки: ^-"Рх + РаМВ» + bl4-»Plt + P2S5. КР2 + IW &12 Pl2 + Рш' Ь15 Pl5 + Р234. . Ь,-^Р,+ Ри|», Ь28->р23+р146И Т. Д. bi-^Pt+PuiB. Получили полуреплику с разрешающей способностью V. В таких планах линейные эффекты смешаны со взаимодействиями третьего порядка, а взаимодействия первого порядка — с взаимодействиями второго порядка. Эта полуреплика имеет преимущества по сравнению с ранее рассмотренной репликой. Возможны двадцать два решения при выборе плана 25-1: хб==х1хй' 9) X6=:X2Xt, 16) == X^XgX^, 2) £5== xxx2, 10) X& = Х^Хд, 17) X6=:XlXzXl, Xfi--- XjX'j, 11) Xg----- x;ixt, 18) Xg----- х^х^х^ 4) хъ = x^xg, 12) xs = —xsxit 19) ж5 = х2х3х^, хъ ~ xixv 13) хъ = XyX^Xg, 20) хъ = —x2x3xv 6) Xg--- 14) X^ ™----- XjX^X.jj 21) Xg — X^XjXgX^, 7) X£ — 15) x^ — х^х^х^у 22) Х^ — —. 8) xi --- X2X%> Мы не станем рассматривать выбор полуреплик 2е-1, 27-1 и т. д. Такими полурепликами редко пользуются на практике. Ведь полуреплика 2е-1 требует 32 опыта, а для экспериментатора выгодны планы 26-2 или 26-3, требующие соответственно 16 и 8 опытов. Поэтому с ростом числа факторов возрастает дробность применяемых реплик. Заметим, что при построении главных полуреплик в определяющий контраст надо включать наибольшее число факторов. Построение 1/4-реплик мы рассмотрим в следующем разделе. 7.4. Выбор 1/4-реплик. Обобщающий определяющий контраст Дорогой читатель, приступая к этому параграфу, вам придется запастись еще большим терпением. Но вы будете вознаграждены, ибо с увеличением дробности не только возрастают ваши усилия, но и уменьшается число опытов. А ради этого стоит пс трудиться и тщательно разобраться в выборе 1/4-реплик. При исследовании влияния пяти факторов можно поставить не 16 опытов, как в предыдущем примере, а только 8, т. е. воспользоваться репликой 25-2. Здесь возможны двенадцать решений, если ж4 приравнять парному взаимодействию, а хъ — тройному:
Допустим, выбран пятый вариант: и хъ=ххх2хъ. Тогда определяющими контрастами являются: 1 =xlx:,xi и \.~ххх2хъхъ. Если перемножить эти определяющие контрасты, то получится третье соотношение, задающее элементы столбца 1 Чтобы полностью охарактеризовать разрешающую способность реплики, необходимо записать обобщающий определяющий контраст 1 = Система смешивания определяется умножением обобщающего определяющего контраста последовательно на х1, х2, ха и т. д. Д/j ——■ Д/дД/^ ■ X- - Х^Х^Х^у л* —■ /у /м л* /у ■ /у /у - /у /у -у* — Л1 Л1 Л» — Я» Я» ---------------------- Л* /М Л1 /М ЛИ -— --- 6--------- 12 ГГ5' - _. Т Т Т Т — л» /у» _____ л» л» б--- ^1*^3 4 6---- •*'2ti4--- 3» Л* л» ------------------------ 1*11*11* --------------------------- И* И* И* ----------------------------- -7* -7* 1 2---- 2 3 4------ 1 4 6 ----- 3 5' Д/^З/^ - ---------------- Получается довольно сложная система смешивания линейных эффектов с эффектами взаимодействия первого, второго, третьего и четвертого порядков. Если, например, коэффициенты ^12 Pl2+ P234+ P145+ Рзб И Ь1Ъ -> Р15+ Р345 124+ ргз отличаются от нуля, то возникают сомнения, можно ли пренебрегать другими парными взаимодействиями, с которыми смешаны линейные эффекты. Тогда следует поставить вторую серию опытов, выбрав нужным образом другую 1/4-реплику. При этом можно воспользоваться методом «перевала». Смысл этого метода заключается в том, что вторая четверть-реплика получается из первой путем изменения всех знаков матрицы на обратные. Тогда в обобщающем определяющем контрасте тройные произведения имеют знак, противоположный их знаку в первой четверть-реплике. Тройные произведения определяют парные взаимодействия в совместных оценках для линейных эффектов. Усредняя результаты обеих четверть-реплик, можно получшь линейные эффекты, не смешанные с парными взаимодействиями. Пример 2. Для дополнения 1/4-реплики, заданной определяющими контрастами l=x1x3xi и l=x1x2xsxs, можно использовать реплику, заданную генерирующими соотношениями х4=—ххх2 и х6=—х^х^, реплику, заданную генерирующими соотношениями х4=—ххх3 и х5=хгх2х3) реплику, заданную генерирующими соотношениями х4=х1х3 и х5=—хгх2х3. В случае х4=—ххх2 и х-а = —ххх2хъ обобщающий определяющий контраст запишется в виде \ = —%1x2xi=—xlx2x3x6=+xixix6. Посмотрим, какой будет система смешивания = Х2Хд = —Х2Х3Х^ = -^-XiXijXiXg, х2 = ~Х1Х4 = —Х]ХгХъ = +^2X3X4X5, Хд = ХХХ2Х3Х^ —XХХ2Х$ -1-.г4.гГ), £4 = ХХХ2 ^ —Xi.ro.r3.r4.r5 = -1-.Тд.гй, = —X1X2XiX5 = —X1X2XS = +Х3Х4. Сложим две четверть-реплики xi = —х2хг = х3х4 = ^x1x3xix5 = х1х2х1х5, Х1 — = xvTb = +x2xsxix5 — x1x2xsxi и т. д. Ясно, что дополнение первой 1/4-реплики второй не привело к улучшению ситуации, а, напротив, осложнило ее, так как линейные эффекты смешиваются с двумя парными взаимодействиями и уничтожаются тройные взаимодействия. Если исследовать 1/4-реилику, заданную генерирующими соотношениями 24= —хххг и xb~xjx2x3, то обобщающим контрастом в этом случае явится 1=—x1x3xi=x1x3x3xb= —х2х4хъ. Система смешивания будет Хг = —X3Xt - X2XgXg = —ХгХ2ХлХ6, X-i : —XуХ%ХgX^ : XXX3X^ = —x^x^, X3 = —XtXi = хгх2х5 ~ —x2xaxix6, xi — —хгх3 = x1xix3xix6 = —X2X&, Хъ = —XjX3XiXl = xxx2x3 = —X2Xt, X 5= Х2Х$Х4 = X3xt = —X, Я1ХЬ ~ —X3X4.XS = X2XS — —xlx2xi' При сложении двух 1/4-реплик получается следующая картина: 6i-*Pi + Pa*s. *>*->p4 + Pi23«. Ь12 р12 + pjs, &а -> Pa + Рш> Рь + Ри», -> Pis + Р2» и т. д. бз-^Рз + Рш. Мы получили план с разрешающей способностью IV и освободили линейные эффекты От смешивания с парными взаимодействиями. В случае 1/4-реплики, заданной генерирующими соотношениями х4 = =х1ха и хй——ххх2х3 и обобщающим определяющим контрастом \=x1xixi= = —ххх2х3хь=—х2х4хъ, получается следующая система смешивания: Xj -—— Х3Х^ ' х2хз«С 1 -—— ~"XxX2X^Xgj X2 — X^X2X3X^ - —ХХХ3ХЪ = — S3 — x Iх 4 — — XyX2Xg — — X2X3X4X^1 = X±X3 = —XXX2X3X4X^ : —x.,x§, x5 = ■ —З^З^З = — X^X2 = : —XjX^XQ, — — X2X3 = —£ При сложении двух 1/4-реплик получаем bi-*.Pi+p34, ^-^Pi+Pw. 6ia-^Pl2 + p234> ^а-*р2 + р12м, * Ьб-^Рь+Ршб. Ьп"^р1б+рз«И т. д. Ьз-^рз + р!!, Итак, линейные эффекты освобождаются от совместных оценок с тройными эффектами взаимодействий и в некоторых случаях — с парными. Такое планирование целесообразно применить в том случае, если ставится задача освободить все линейные эффекты от взаимодействий второго порядка И два линейных эффекта (в данном случае Ь2 и 66) — от взаимодействий первого порядка. Таким образом, для дополнения 1/4-реплики до 1/2-реплики, если есть подозрения, что эффекты взаимодействия первого порядка отличаются от нуля, нужно взять вторую четверть-реплику с обобщающим контрастом, в котором два тройных произведения имеют отрицательный знак, так как тройные произведения определяют парные взаимодействия в совместных оценках для линейных эффектов. Однако можне нредетавить в«б«ж?аквй «лучай, кввда целесообразно освободить линейные эффекты от эффектов взаимодействия второго порядка и только часть из линейных эффектов (например, Ь2 и"68) от парных взаимодействий. Тогда нужно выбрать 1/4-реплику таким образом, чтобы в обобщающем определяющем контрасте произведение четырех членов имело отрицательный знак, так'как это произведение определяет тройные взаимодействия в совместных оценках для линейных эффектов. Теперь рассмотрим пример реплики 25-2. Пример 3. Применение плана 25_а относится к оптимизации процесса получения одного производного пиперазина по схеме В. Было решено при планировании эксперимента варьировать пятью факторами, представленными в табл. 7.6. Параметром оптимизации служил выход реакции в процентах. Таблица 7.6
В табл. 7.7 приведена матрица планирования эксперимента. В данном случае при планировании использована 1/4-реплика от полного факторного эксперимента 25. При этом ставится 8 опытов вместо 32. Матрица задана генерирующими соотношениями ^4=х1х2х3, х5=—хххг и имеет обобщающий контраст 1=x1x2x3xi= —х1х2х5= —х3х1хь. Выбрано генерирующее соотношение хъ= — ххх2, поскольку взаимодействия ххх3 и х2х3 предполагались существенными. Совместные оценки такой 1/4-реплики h -»• Pi - р2» + р2М - Pl845.»5 -* Р» - Pl2 - Рм + Pl2S45, *>2 Ра - Pli + Put - P2MS. Ьп-Pi»+ ра4 - Р285 ~ Pl«, Ъ3 -> Рз - Р«+ Pl24 - Pirn. &14 Pl4 + Р28 - Р24& ~ Рш-
7.5. Реплики большой дробности Если вы, наш терпеливый читатель, осилили два предыдущих параграфа, вы сможете выбрать реплику любой дробности. Процедура выбора совершенно аналогична. При выборе 1/8-реплики 26-3 можно воспользоваться вектор- столбцами трех взаимодействий, например, так: 1) £4--- Х^Х.,, Х^ ----- ХуХ^, 2) Х^ = X^Xg, Я-5 == X^Xg, 3) х4---- Х^Х^, Х§ — х^х^ 4) X^--- X-^X^t Х^ — x,xs, Для каждого из этих решений можно сделать шесть перестановок. Итого получается 24 возможности выбора 1/8-реплики. Это при условии, что мы всюду выбираем положительные генерирующие соотношения. Из четырех приведенных выше решений наименее удачно первое, поскольку все линейные эффекты смешиваются с парными взаимодействиями. Если априорно известно, что из всех взаимодействий наиболее существенно хгхг, то нужно выбрать второе решение, если хххъ — третье, а если х^с3 — четвертое. Допустим, мы избрали четвертое решение, предполагая, что из факторов ж4, х5, х6 наиболее существенным является х4. Приравняем х4 тройному взаимодействию и запишем генерирующие соотношения Х4 XуХ, X, Xq — XjX^. Ограничимся парными и тройными взаимодействиями. Для 1/8-реплики с генерирующими соотношениями — Xg—X^Xg имеем следующие определяющие контрасты: 1 ' ^ --- Xj^Xg у 1 -- XjXjjiCQ % Если попарно перемножить эти определяющие контрасты, то получим 1 = хях4хГ1; 1 ~=:: x^x^X q ', 1 х2хяхъх6.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.184 (0.147 с.) |
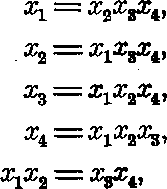
 Х1Х2------ 3-8^41
Х1Х2------ 3-8^41






