Загальний опис проблем предметної області.

При використанні контурних ознак для аналізу і розпізнавання зображень на першому етапі потрібно вирішити задачу виділення контурів зображень. Рішення розбивається на наступні кроки:

1) виявлення перепадів яскравості на монохроматичному зображенні (або перепадів координат кольору окремо в кожному каналі кольорового зображення) і виділення граничних точок об'єктів зображення;

2) усунення розривів граничних точок зображення;

3) простежування і аналітичний опис коду контурів зображень, отриманих апроксимацією виявлених граничних точок.

При вирішенні задачі виявлення граничних точок попередньо потрібно застосувати лінійні або нелінійні методи попереднього підкреслення перепадів яскравості [8,11,13]. Серед лінійних методів підвищення контрасту перепадів широко застосовуються градієнтні методи з використанням операторів Превітта, Щарра, Собеля, Робертса, що враховують орієнтацію границі [8-10]. До інших лінійних методів належать методи частотної фільтрації, інваріантні до орієнтації перепадів, наприклад, оператори Гаусса з імпульсною характеристикою, що визначає вагові функції гауссової форми, запропоновані Аргайлом і Маклеодом, оператори Лапласа, фільтри верхніх і нижніх частот. З нелінійних диференціальних фільтрів широке поширення отримали фільтри першого, другого і третього порядків Робертса, Собела, Кірша, Лапласа, Щарра [8-11,]. Уолліс [8] запропонував використовувати нелінійний метод підвищення контрастності перепадів, заснований на гомоморфной обробці зображення. Розенфельдом були розроблені нелінійні методи підвищення контрасту і виділення перепадів, засновані на обчисленні добутку деяких середніх різного порядку [9]. Перераховані методи не враховували функцію яскравості (кольори) зображення в місцях виділення перепадів. Хюккель розробив процедуру апроксимації двовимірного перепаду. В результаті чого оператор Хюккеля дає досить хороші характеристики навіть на зашумленних зображеннях [8].

Після підкреслення перепадів яскравості виконується порогова обробка і виноситься рішення про виявлення (не виявлення) граничних точок об'єктів зображення. Для обчислення порогових значень виявлювачів використовуються власні значення і (або) власні вектори деяких матриць, отриманих за значеннями профільтрованих зображень. Крім однопорогового виявлювача границь, часто використовується двухпороговий виявлювач границь Кєнні.

Тим не менш, як підкреслювалося в оглядовій роботі американського професора А. Розенфельда [9] «до сих пор нет сколько-нибудь удовлетворительной модели краев областей цифровых изображений, хотя она бы была очень полезна при построении оптимальных операторов обнаружения границ». Тому всі розглянуті вище методи підкреслення і виявлення граничних точок є суто евристичними. Відсутність адекватних моделей сигналів і перешкод для більшості реальних сцен призводить до того, що в загальному випадку невідомі оптимальні вирішальні процедури виявлення граничних точок зображень.

Оптимальний виявлювач граничних точок в межах локально однорідної ділянки сцени в загальному випадку повинен містити фоноподавляючі, узгоджені і порогові ланки. Як критерій роботи такого детектора часто вибирається критерій Неймана-Пірсона [42-44]. Відповідно до нього виявлювач повинен забезпечувати максимум ймовірності правильного виявлення при заданому рівні ймовірності помилкової тривоги. В роботах Хафизова Р.Г. [15] розглянуто метод узгоджено-виборчої фільтрації для квазіоптимального виділення контурів зображень з прямолінійними межами, базується на гіпотезі експоненціально-косинусном автокореляційної функції фонових шумів і слабкою інформативності низькочастотної частини спектра зображення.

Внаслідок статистичних неоднорідностей окремих областей об'єктів і фону зображення об'єктів стають багатозв'язними через утворених порожнин і розривів, при цьому сильно спотворюється лінія контуру. Руйнування через зазначених факторів однозв’язної структури цифрового впливу призводять до того, що замість одного контуру, що описує форму вихідного зображення, ми отримуємо набір контурів різної форми в межах контуру одного зображення. Тому для поліпшення якості виявлення меж на другому кроці завдання виділення контурів зображень необхідно застосовувати додаткові заходи, пов'язані з усуненням розривів граничних точок зображень об'єктів і фільтрацією неправдивих контурних ліній. Серед відомих підходів усунення розривів граничних точок використовуються: метод релаксації [13], заснований на понятті сили границі та пов'язаним з ним виявленням і відновленням розірваної границі в межах певної локальної області; метод морфологічного аналізу зображень з використанням операторів злиття і поділу[13], що згладжують межі об'єктів без істотних змін їх площ. При виявленні граничних точок можна використовувати також апріорну інформацію про форму контурних ліній зображень. Велике поширення набуло перетворення Хоха для виявлення кордонів заданої форми. В роботах Фурмана, Єгошина [14-22] розглянуті питання квантування кордонів зображень об'єктів, прямолінійної протяжної форми.

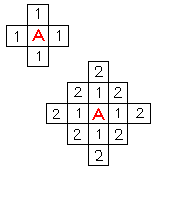
Завершальним кроком етапу виділення контурів зображень є процедура простежування і безпосереднього формування аналітичного опису коду контурів. В якості базового алгоритму простежування лінії контуру, при якому послідовно, без розривів виділяються контурні точки зображення і формується код контуру, доцільно використовувати алгоритм, запропонований Розенфельдом [9]. Серед інших відомих алгоритмів простежування можна виділити алгоритм «жук» (Рисунок 1.2.1), алгоритм пошуку в чотирьох напрямках [13] (Рисунок 1.2.2), алгоритми пошуку по круговій і трикутної траєкторіях, алгоритм пошуку по графу [13].

 

Рисунок 1.2.1 - Алгоритм пошуку «Жук»

 

Рисунок 1.2.2 - Алгоритм пошуку «в чотирьох напрямках»

При аналітичному описі отриманого контуру цифрового зображення формується дискретний сигнал. Для плоских зображень кожен елемент коду контуру можна розглядати як спрямований відрізок (елементарний вектор (ЕВ)) в деякому лінійному двовимірному просторі (d = 2, де d - розмірність ЕВ). Вибір лінійного простору для представлення ЕВ значно визначає всі характеристики результатів, отриманих при вирішенні завдань другого етапу контурного аналізу зображень, таких як: виявлення, вирішення, розпізнавання та оцінка параметрів перетворень [32-34].

Один з перших способів кодування ЕВ був запропонований в роботах Фрімена [52-53], в залежності від восьми можливих напрямків на квадратної сітківці кожен стандартний елементарний вектор кодується відповідним цілим числом від 0 до 7. Алгоритм показано на рисунку 1.2.3.

Рисунок 1.2.3 - Ланцюговий код Фрімена

Кодування поточного ЕВ може проводитися також двома його проекціями на осі координат з початком відліку, поєднаним з початком ЕВ. В роботах Фурмана Я. Л. [14-22] запропоновано ЕВ контуру задавати вісьмома комплексними числами. Даний код згодом отримав назву «Комплекснозначний код контуру». Комплекснозначне завдання коду контуру, тобто вибір N-мірного лінійного дискретного комплексного простору для опису контурів плоских зображень (де N - кількість ЕВ в складі контуру), дозволило використовувати добре розроблені методи обробки безперервних і дискретних комплекснозначних сигналів в радіотехнічних системах для вирішення задач аналізу комплекснозначних контурів зображень [46-51].

В даний час теорія контурного аналізу, що охоплює питання завдання, перетворення, добування інформації з плоских зображень контурів і групових точкових об'єктів і представляє розділ теорії комплекснозначних сигналів, досить добре розвинена і апробована в роботах: Фурмана Я.А., Кревецького А.В., Передреева А.К., Роженцова А.А., Хафизова Р.Г., Єгошина И.Л. [14-22].

Актуальність даної теми.

В рамках цієї роботи розробляється метод і алгоритми автоматизованого розпізнавання образів на базі алгоритмів контурного аналізу. Досліджуються у окремому завданні: розпізнавання Герба України. Методи що розробляються носять загальний характер і можуть застосовуватися для розпізнавання широкого кола об'єктів на базі шаблонів - контурів. У методі застосовується еквалізація що дозволяє відкоригувати зображення. Застосовуються фільтри для усунення паразитних шумів. Також в даній роботі використовуються методи Віоли і Джонса, які дозволяють навчити нейронну мережу і отримати на виході каскад Хаара, завдяки якому можна розпізнавати той же об'єкт (Герб України). І це дозволить провести порівняльний аналіз отриманих результатів від розробленого методу і від навченого каскаду, який використовує зовсім інші методи виявлення об'єктів. Після закінчення дослідження, будуть запропоновані рекомендації для використання того чи іншого методу, в таких чи інших завданнях. Так як в Україні поки що не ведуться такого роду розробки, на відміну від західних країн, в яких комп'ютерний зір поступово знаходить своє застосування, і дозволяє зекономити на виробництві значні суми грошей. Даною роботою можуть зацікавитися наші державні військові служби або комерційні підприємства, з метою автоматизації процесів та зниженні витрат на виробництві, шляхом впровадження систем комп'ютерного зору і базуючись на дослідження даної роботи, знизити ризик вибору непідходящого методу детектування об'єктів.

 

 

 

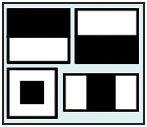
АНАЛІЗ ІСНУЮЧИХ АНАЛОГІВ

Метод Віоли-Джонса

Метод П.Віоли і М.Джонса, був опублікований в 2001. Цей підхід до детектування об'єктів на зображенні комбінує чотири ключові концепції:

- Прості прямокутні функції, які називаються функціями Хаара.

- Інтегральне зображення для швидкого виявлення функції.

- Метод машинного навчання AdaBoost.

- Каскадний класифікатор для ефективного поєднання множинних функцій.

Особливості, які використовували Віола і Джонс, базуються на вейвлетах Хаара. Вейвлети Хаара представляють собою прямокутні хвилі однакової довжини (один високий інтервал і один низький інтервал). У двох вимірах, прямокутна хвиля являє собою пару сусідніх прямокутників - один світлий і один темний [23-30].

Рисунок 2.1.1 – Приклад функцій Хаара

Фактично прямокутні комбінації, що використовуються для візуального виявлення об'єкта не є справжніми вейвлетами Хаара. Замість цього, вони містять прямокутні комбінації, які краще підходять для візуальних завдань розпізнавання. Через цю різницю, ці функції називаються функціями Хаара (або Хаар-подібними функціями), а не вейвлетами. Рисунок 2.1.1 показує ті функції, що використовуються в OpenCV.

Наявність функції Хаара визначається за допомогою вирахування середнього значення області темних пікселів із середнього значення області світлих пікселів. Якщо різниця перевищує поріг (визначається в процесі навчання), тоді кажуть, що функція є існуючою.

Щоб ефективно визначити наявність і відсутність сотень функцій Хаара на кожній локації зображенні і в декількох масштабах, Віола і Джонс використовували технологію Інтегрального Зображення. Загалом, «інтеграція» означає складання маленьких блоків разом. В цьому випадку, маленькі блоки є піксельними значеннями. Інтегральне значення для кожного пікселя є сума всіх пікселів над ним і ліворуч від нього. Починаючи з лівого верхнього кута і здійснюючи обхід вправо і вниз, все зображення може бути інтегровано з кількома цілочисельними операціями на піксель.

Рисунок 2.1.2 – Трюк Интегрального Изображения.

Як показано на Рисунок 2.1.2.a, після інтеграції, значення в кожнго пікселя (х, у) містить суму всіх піксельних значень всередині прямокутної області, яка має один кут у лівій верхній частині зображення і інший в положенні (х, у). Щоб знайти середнє піксельне значення в цьому прямокутнику, необхідно тільки розділити значення в (х, у) на площу прямокутника. Але що якщо цікавлять підсумовані значення для деяких інших прямокутників, які не мають жодного кутка в лівій верхній частині зображення, Рисунок 2.1.2.b ілюструє вирішення цієї проблеми. Припустимо, потрібно дізнатися підсумовані значення в D = (x4, y4) - (x2, y2) - (x3, y3) + (x1, y1) [28-34].

Для вибору конкретних функцій Хаара і встановлення граничних рівнів, Віола і Джонс використовують метод машинного навчання під назвою AdaBoost. AdaBoost комбінує багато «слабких» класифікаторів з метою створення одного «сильного» класифікатора. «Слабкий» тут означає такий класифікатор, який отримує правильну відповідь ненабагато частіше, ніж випадкове вгадування. Це не є добре. Але якщо у вас є безліч таких слабких класифікаторів, і кожен з них «висунув» остаточну відповідь трохи у вірному напрямку, ви можете отримати серйозну, комбіновану силу для досягнення коректного рішення. AdaBoost вибирає набір слабких класифікаторів для об'єднання і привласнює кожному з них свою вагу. Ця зважена комбінація і є сильним класифікатором. Віола і Джонс об'єднали серії класифікаторів AdaBoost як послідовність фільтрів, показаних на Рисунку 2.1.3, що особливо ефективно для класифікації областей зображення. Кожен фільтр є окремим класифікатором AdaBoost з досить невеликим числом слабких класифікаторів [28-34].

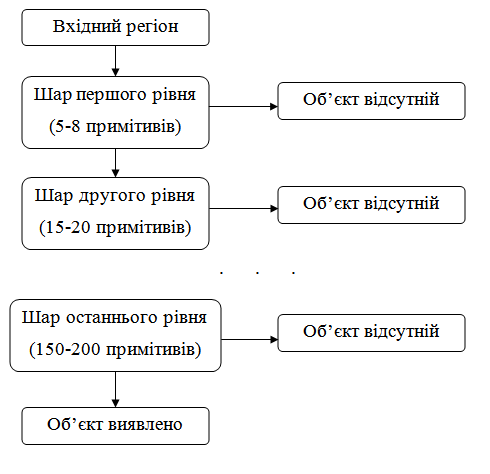
Рисунок 2.1.3 – Каскад фільтрів Хаара

 

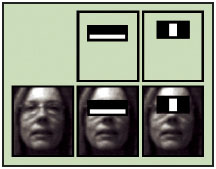
Прийнятий поріг на кожному рівні встановлюється досить низьким, щоб пройти всі (або майже всі) особові зразки в тренувальному наборі. Фільтри на кожному рівні навчені класифікувати тренувальні зображення, які пройшли всі попередні етапи (навчальна вибірка являє собою велику базу осіб, може бути, близько тисячі або близько до цього). Під час роботи, якщо якийсь будь-який з цих фільтрів не пропускає область зображення, то тоді область відразу ж класифікується як «Об’єкт відсутній». Коли фільтр пропускає область зображення, вона переходить до наступного фільтру в послідовності. Область зображення, що пройшли через всі фільтри, класифікуються як «Об’єкт виявлено». Віола і Джонс називали це фільтрацією ланцюга каскаду.

Порядок фільтрів в каскаді грунтується на ваговому значенні, які присвоює AdaBoost. Більш важкі зважені фільтри йдуть в першу чергу, з метою якомога більш швидкого усунення областей що не містять цільового об’єкта. Рисунок 2.1.4 показує перші дві функції Хаара, що накладені на обличчя. Перший налаштовує дальню область щік більш «світлою», ніж область очей. Другий використовує факт того, що носова перегородка більше світла, ніж очі.

Рисунок 2.1.4 – Накладання функцій Хаара на зображення

Метод SURF

SURF вирішує дві задачі - пошук особливих точок зображення і створення їх дескрипторів, інваріантних до масштабу і обертанню. Це означає, що опис ключової точки буде однаково, навіть якщо зразок змінить розмір і буде обернутий. Крім того, сам пошук ключових точок володіє інваріантністю. Так, що повернений об'єкт сцени має той же набір ключових точок, що і зразок.

Метод шукає особливі точки за допомогою матриці Гессе. Детермінант матриці Гессе (т.зв. гессіан) досягає екстремуму в точках максимальної зміни градієнта яскравості. Він детектує плями, кути і краї ліній. На рисунку 2.2.1 зображені особливі точки зображення будівлі, знайдені за допомогою матриці Гессе. Діаметр кола показує масштаб особливої ​​точки, а зелена лінія - напрямок градієнта яскравості.

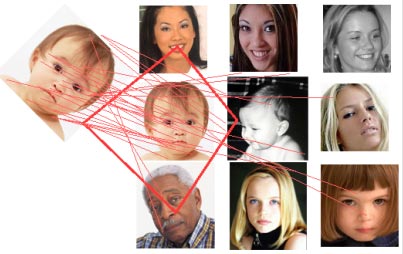
Рисунок 2.2.1 – Особливі точки зображення будівлі

Гессіан інваріантний до обертання. Але не інваріантний масштабу. Тому SURF використовує різномасштабні фільтри для знаходження гессіанів. Для кожної ключової точки розраховується напрямок максимальної зміни яскравості (градієнт) і масштаб, взятий з масштабного коефіцієнта матриці Гессе. Градієнт в точці обчислюється за допомогою фільтрів Хаара.

Після знаходження ключових точок, SURF формує їх дескриптори. Дескриптор являє собою набір з 64 (або 128) чисел для кожної ключової точки. Ці числа відображають флуктуації градієнта навколо ключової точки. Оскільки ключова точка являє собою максимум гессіан, то це гарантує, що в околиці точки повинні бути ділянки з різними градієнтами. Таким чином, забезпечується дисперсія (відмінність) дескрипторів для різних ключових точок.

Флуктуації градієнта околиць ключової точки розраховуються відносно направлення градієнта навколо точки в цілому (по всій околиці ключової точки). Таким чином, досягається інваріантність дескриптора щодо обертання. Розмір області, на якій розраховується дескриптор, визначається масштабом матриці Гессе, що забезпечує інваріантність щодо масштабу.

Флуктуації градієнта також розраховується за допомогою фільтра Хаара.

На рисунку 2.2.2, зліва знаходиться зразок, справа - сцена. Червоні лінії показують максимально схожі особливі точки зразка і сцени. Червона трапеція - показує виявлений на сцені об'єкт.

 

Рисунок 2.2.2 – Приклад роботи SURF

Метод SIFT

Виявлення об'єктів за допомогою методу SIFT полягає в порівнянні зображень по ключових точках.

Схема рішення задачі порівняння зображень:

- На зображеннях виділяються ключові точки і їх дескриптори.

- За збігом дескрипторів виділяються відповідно один одному ключові точки.

- На основі набору ключових точок що співпали будується модель перетворення зображень, за допомогою якого з одного зображення можна отримати інше.

Основним моментом у детектуванні особливих точок є побудова піраміди гаусіан (Gaussian) і різниць гаусіан (Difference of Gaussian, DoG). Гаусіаном (або зображення розмите гаусовим фільтром) є зображення. Різницею гаусіанів називають зображення, отримане шляхом попіксельного віднімання одного гаусіана вихідного зображення від гаусіани з іншим радіусом розмиття [31].

Інваріантність щодо масштабу досягається за рахунок знаходження ключових точок для вихідного зображення, взятого в різних масштабах. Для цього будується піраміда гаусіанів: весь масштабований простір розбивається на деякі ділянки - октави, причому частина масштабованого простору, займаного наступної октавою, в два рази більше частини, займаної попередньої. До того ж, при переході від однієї октави до іншої робиться ресемплінг зображення, його розміри зменшуються вдвічі. Звісно, що кожна октава охоплює безліч гаусіанів зображення, тому будується тільки деяка їх кількість N, з певним кроком по радіусу розмиття. З тим же кроком добудовуються два додаткові гаусіани (всього виходить N +2), що виходять за межі октави. Масштаб першого зображення наступної октави дорівнює масштабу зображення з попередньої октави з номером N.

Паралельно з побудовою піраміди гаусіанів, будується піраміда різниць гаусіанів, що складається з різниць сусідніх зображень в піраміді гаусіанів [31]. Відповідно, кількість зображень в цій піраміді буде N +1.

На рисунку 2.3.1 зліва зображена піраміда гаусіанів, а праворуч - їх різниця. Схематично показано, що кожна різниця виходить з двох сусідніх гаусіанів, кількість різниць на одиницю менше кількості гаусіанів, при переході до наступної октаві розмір зображень зменшується вдвічі.

Рисунок 2.3.1 – Піраміда гаусіанів

 

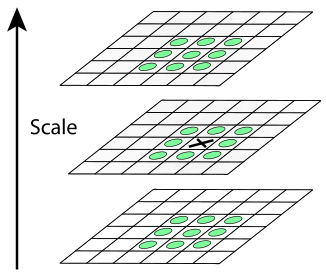
Точка вважається особливою, якщо вона є локальним екстремумів різниці гаусіанів. Для пошуку екстремумів використовується метод, схематично зображений на рисунку 2.3.2.

Рисунок 2.3.2 – Особлива точка

 

Якщо значення різниці гаусіанів в точці поміченої хрестиком, більше або менше за всіх значень в точках, позначених зеленими кружальцями, то ця точка вважається точкою екстремуму.

У методі SIFT дескриптором є вектор. Як і напрямок ключової точки, дескриптор обчислюється на гаусіані, що є найближчою за масштабом до ключової точки, і виходячи з градієнтів в деякому вікні ключової точки. Перед обчисленням дескриптора це вікно повертають на кут напрямку ключової точки, чим і досягається інваріантність щодо поворотів.

.

Рисунок 2.3.3 – Дескриптор ключових точок

 

Отриманий дескриптор нормалізується, після чого всі його компоненти, значення яких більше 0.2, урізуються до значення 0.2 і потім дескриптор нормалізується ще раз. У такому вигляді дескриптори готові до використання.

SIFT дескриптори не позбавлені недоліків. Не всі отримані точки і їх дескриптори будуть відповідати вимогам, що пред'являються. Звісно це буде позначатися на подальшому вирішенні задачі порівняння зображень. У деяких випадках рішення може бути не знайдено, навіть якщо воно існує. Наприклад, при пошуку афінних перетворень (або фундаментальної матриці) за двома зображеннями цегляної стіни, рішення може бути не знайдено через те, що стіна складається з повторюваних об'єктів (цеглин), які роблять схожими між собою дескриптори різних ключових точок. Незважаючи на цю обставину, дані дескриптори добре працюють в багатьох практично важливих випадках.

Метод ORC

Оптичне розпізнавання символів (англ. optical character recognition, OCR) - механічний або електронний переказ зображень рукописного, машинописного або друкованого тексту в послідовність кодів, що використовуються для подання в текстовому редакторі. Розпізнавання широко використовується для конвертації книг і документів в електронний вигляд, для автоматизації систем обліку в бізнесі або для публікації тексту на веб-сторінці. Оптичне розпізнавання тексту дозволяє редагувати текст, здійснювати пошук слова чи фрази, зберігати його в більш компактній формі, демонструвати або роздруковувати матеріал, не втрачаючи якості, аналізувати інформацію, а також застосовувати до тесту електронний переказ, форматування або перетворення в мову. Оптичне розпізнавання тексту є досліджуваною проблемою в областях розпізнавання образів, штучного інтелекту та комп'ютерного зору.

Системи оптичного розпізнавання тексту вимагають калібрування для роботи з конкретним шрифтом; в ранніх версіях для програмування було необхідно зображення кожного символу, програма одночасно могла працювати тільки з одним шрифтом. В даний час найбільше поширені так звані «інтелектуальні» системи, з високим ступенем точності розпізнають більшість шрифтів. Деякі системи оптичного розпізнавання тексту здатні відновлювати початкове форматування тексту, включаючи зображення, колонки та інші нетекстові компоненти.

Точне розпізнавання латинських символів в друкованому тексті в даний час можливо тільки якщо доступні чіткі зображення, такі як скановані друковані документи. Точність при такій постановці завдання перевищує 99%, абсолютна точність може бути досягнута тільки шляхом наступного редагування людиною. Проблеми розпізнавання рукописного «друкарського» і стандартного рукописного тексту, а також друкованих текстів інших форматів (особливо з дуже великим числом символів) в даний час є предметом активних досліджень.

Порівняльна характеристика

Таблиця 2.5.1 – Порівняння аналогів

Властивості	Назва методу
Віоли-Джонса	SURF	SIFT	ORC
Інваріантність до масштабу	+	+	+	+
Інваріантність до обертання	-	+	+	+
Чутливість до освітлення	-	+	+	+
Ризик перенавчання	+	-	-	-
Детектування декількох об’єктів одноразово	+	-	-	+
Складність	O(n^3)	O(n^3)	O(n^3)	O(n^3)
Час на створення еталону	5-30 діб.	30-60 хв.	30-60 хв.	2-8 год.

 

 

МЕТА КВАЛІФІКАЦІЙНОЇ РОБОТИ

Метою магістерської роботи, є дослідження методів контурного аналізу, вивчення проблем та досягнень в цій галузі. Розробка автоматизованої системи розпізнавання об’єктів на базі алгоритмів контурного аналізу, яка дозволить провести аналіз ефективності двох методів розпізнавання об'єктів за допомогою контурного аналізу та каскаду Хаара. Так як на сьогоднішній день, немає універсальних методів, необхідно визначити ефективність та швидкодію роботи методів, виявити переваги і недоліки методів.

 

 

 

ПОСТАНОВКА ЗАДАЧІ

Для досягнення мети необхідно:

1. Вивчити предметну область;

2. Провести огляд аналогів;

3. Навчити нейронну мережу, за допомогою утиліт що поставляються бібліотекою OpenCV, та отримати на виході каскад Хаара.

4. Розробити метод автоматизованого розпізнавання об’єктів на базі алгоритмів контурного аналізу.

5. Розробити програмний продукт, в якому використовуються два методи детектування об'єктів за допомогою «Контурного аналізу» та «Каскаду Хаара».

6. Провести аналіз ефективності детектування обох методів. Скласти таблицю ефективності з отриманих результатів.