
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм нахождения базиса системы векторов
Для того, чтобы найти базис системы векторов A1,A2,...,An необходимо: § Составить соответствующую системе векторов однородную систему уравнений A1x1+A2x2+...+Anxn =Θ § Привести эту систему -------------------------------------------------------------------------------------------- 19. Понятие векторного пространства n-мерным евклидовым векторным пространством называется векторное пространство в котором заданы операции сложения векторов, умножение вектора на число и скалярного умножения векторов, удовлетворяющие аксиомам групп I, II, III и группы IV. Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Теорема. (О разложении вектора по базису.) Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. Доказательство. 1) Пусть L произвольная прямая (или ось) и Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора
Так как 20. Понятие ортогональной системы векторов, ортогонального базиса. Нахождение координат вектора в ортогональном базисе. Базис
Базис В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис. Если длина вектора равна единице, он называется нормированным вектором: (x, x) = 1, |x| = 1. Если все векторы системы векторов нормированы, то система векторов называется нормированной системой. Если векторы системы векторов e 1, e 2, ..., e n попарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (e i, e j) = 0, если i ≠ j, (e i, e i) = 1. Если e 1, e 2, ..., e n — ортонормированная система и x = x 1 e1 + x 2 e2 +... + xn e n — разложение вектора x по этой системе, то x i =(x, e i).
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.173 (0.007 с.) |
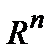 ,евклидова пространства
,евклидова пространства  . Разложение вектора в
. Разложение вектора в 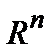 по векторам его базиса. Теорема о единственности разложения вектора в данном базисе.
по векторам его базиса. Теорема о единственности разложения вектора в данном базисе. –базис
–базис  . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора 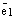 и
и  коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то 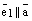 . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как  , то найдется (существует) такое число
, то найдется (существует) такое число 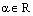 , что
, что  и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора 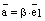 , где
, где 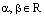 . Тогда
. Тогда  и используя закон дистрибутивности, получаем:
и используя закон дистрибутивности, получаем: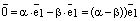 .
. , ч.т.д.
, ч.т.д.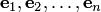 евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.
евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е. при
при 



