
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Печатается по решению Ученого совета и редакционно-издательского совета Института экономики, управления и права (г. Казань)Стр 1 из 8Следующая ⇒
УДК 330.43 (075.8) ББК 65вбя73 Э40 Печатается по решению Ученого совета и редакционно-издательского совета Института экономики, управления и права (г. Казань) А.В. Костромин Э40 Эконометрика: Курс лекций. - Казань: Изд-во «Таглимат», 2004. - 136 с. ISBN 5-8399-0094-Х Курс лекций к. т. н, доц. Костромина А.В. предназначен для студентов и преподавателей экономических факультетов высших учебных заведений. УДК 330.43 (075.8) ББК 65вбя73 © Институт экономики, управления и права (г. Казань), 2004 © Костромин А.В., 2004 ISBN 5-8399-0094-Х Содержание Введение 4 ПАРНАЯ РЕГРЕССИЯ 6 1. Спецификация модели 6 2. Оценка параметров линейной регрессии 11 3. Предпосылки МНК (условия Гаусса-Маркова) 17 4. Оценка существенности параметров линейной регрессии и корреляции 18 5. Интервалы прогноза по линейному уравнению регрессии 25 6. Нелинейная регрессия 28 II. МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ 36 2.1. Оценка параметров линейного уравнения множественной регрессии 39 2.2. Частные уравнения регрессии 46 2.3. Анализ качества эмпирического уравнения множественной линейной регрессии 49 2.4. Специфические модели 58 2.5. Гетероскедастичность. 71 2.6. Автокорреляция остатков 78 2.7. Фиктивные переменные в регрессиональных моделях 85 III. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ 92 3.1. Структурная и приведенная формы модели 94 3.2. Проблема идентификации 95 3.3. Оценивание параметров структурной модели 100 3.4. Применение систем эконометрических уравнений 104 IV. ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ 109 4.1. Выявление структуры временного ряда 109 4.2. Динамические эконометрические модели 125 Список рекомендуемой литературы 135 ВВЕДЕНИЕ Эконометрика - это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели реальных экономических явлений. Эконометрика позволяет найти количественное подтверждение либо опровержение того или иного экономического закона либо гипотезы. Эконометрика как научная дисциплина зародилась и получила развитие на основе слияния экономической теории, математической экономики и экономической и математической статистики. По словам Р.Фриша: «... каждая из трех отправных точек - статистика, экономическая теория и математика-необходимое, но недостаточное условие для понимания количественных соотношений в современной экономической жизни. Это единство всех трех составляющих. И это единство образует эконометрику».
Спецификация модели Регрессия представляет собой зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от функциональной зависимости, когда каждому значению независимой переменной х соответствует одно определенное значение величины у, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины у. В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии. Простая регрессия представляет собой регрессию между двумя переменными - у и х, т.е. модель вида:
где у - зависимая переменная (результативный признак); х - независимая, или объясняющая переменная (признак-фактор, или регрессор). Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида:
Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Из всего круга факторов, влияющих на результативный признак, необходимо выделить наибольшие, существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Например, выдвигается гипотеза о том, что величина спроса на товар находится в обратной зависимости от цены х, т.е. Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как закономерность лишь в среднем по совокупности наблюдений. (Например, если зависимость спроса у от цены х: у = 5000 – 2·х означает, что с ростом цены на 1 д.е. спрос в среднем уменьшается на 2 д.е.). В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи. В каждом отдельном случае величина у складывается из двух слагаемых:
где yj - фактическое значение результативного признака; Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее порождают 3 источника: спецификация модели, выборочный характер исходных данных и ошибки измерения. Например, зависимость спроса от цены точнее следует записывать так:
В данном случае слева записано просто у, что означает фактическое значение, а не Ошибки спецификации. Это прежде всего неправильно выбранная форма модели. В частности, зависимость спроса от цены может быть выражена линейно
но возможны и другие соотношения, например
Ошибки спецификации тем меньше, чем в большей мере теоретические значения признака подходят к фактическим данным. К ошибкам спецификации относится также недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной. Например, спрос на конкретный товар может определяться не только ценой, но и доходом надушу населения. Ошибки выборки. Исследователь при установлении связи между признаками имеет дело с выборочными данными. При изучении экономических процессов данные в исходной совокупности часто являются неоднородными. В этом случае уравнение регрессии не имеет практического смысла. Поэтому для получения хорошего результата из выборки исключают единицы с аномальными значениями исследуемых признаков. Ошибки измерения. Представляют наибольшую опасность в практическом использовании методов регрессии. Ошибки спецификации можно уменьшить, изменяя форму модели, ошибки выборки - увеличивая объем исходных данных, ошибки измерения сводят на нет все усилия по количественной оценке связи между признаками. Например, статистическое измерение дохода на душу населения может иметь ошибку в результате наличия сокрытых доходов. Другой пример: органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. В эконометрических исследованиях предполагается, что ошибки измерения сведены к минимуму. Поэтому основное внимание уделяется ошибкам спецификации модели. В парной регрессии выбор вида математической функции (1) может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным. Графический метод достаточно нагляден. Он основан на поле корреляции. Рассмотрим типы кривых.
Используются и другие типы кривых:
Аналитический метод выбора типа уравнения регрессии основан на изучении материальной природы связи исследуемых признаков. Пусть, например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х. Все потребление электроэнергии можно подразделить на 2 части: - не связанное с производством продукции a; - непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска bx;
Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида:
Разделив на х, получим удельный расход электроэнергии на единицу продукции zx=у/х;
Это равносторонняя гипербола. Аналогично затраты предприятия могут быть условно-переменные, изменяющиеся пропорционально изменению объема продукции (расход материала, оплата труда и др.) и условно-постоянные, не изменяющиеся с изменением объема производства (арендная плата, содержание администрации и др.). Соответствующая зависимость затрат на производство y от объема продукции х характеризуется линейной функцией. y=a+bx, а зависимость себестоимости единицы продукции zx от объема продукции - равносторонней гиперболой:
Экспериментальный метод используется при обработке информации на компьютере путем сравнения величины остаточной дисперсии Dост , рассчитанной на разных моделях. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии факторов:
Чем меньше Dост , тем меньше наблюдается влияние прочих факторов, тем лучше уравнение регрессии подходит к исходным данным. При обработке данных на компьютере разные математические функции перебираются в автоматическом режиме, и из них выбирается та, для которой Dост является наименьшей. Если Dост примерно одинакова для нескольких функций, то на практике выбирают более простую, так как она в большей степени поддается интерпретации и требует меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений. Для рядов динамики, ограниченных по протяженности - 10, 20, 30 лет, - предпочтительна модель с меньшим числом параметров при х. Таблица 1
Система нормальных уравнений будет иметь вид:
Решая её, получаем а = -5,79, b = 36,84. Уравнение регрессии имеет вид:
Подставив в уравнение значения х, найдем теоретические значения y (последняя колонка таблицы). Величина а не имеет экономического смысла. Если переменные х и у выразить через отклонения от средних уровней, то линия регрессии на графике пройдет через начало координат. Оценка коэффициента регрессии при этом не изменится:
В качестве другого примера рассмотрим функцию потребления в виде: С = К·у + L где С - потребление, у -доход, K, L – параметры. Данное уравнение линейной регрессии обычно используется в увязке с балансовым равенством: y = C + I – r, где I – размер инвестиций, r – сбережения. Для простоты предположим, что доход расходуется на потребление и инвестиции. Таким образом, рассматривается система уравнений:
Наличие балансового равенства накладывает ограничения на величину коэффициента регрессии, которая не может быть больше единицы, т.е. К ≤ 1. Предположим, что функция потребления составила:
Коэффициент регрессии характеризует склонность к потреблению. Он показывает, что из каждой тысячи рублей дохода на потребление расходуется в среднем 650 руб., а 350 руб. инвестируется. Если рассчитать регрессию размера инвестиций от дохода, т.е. 0,65 + 0,35 = 1 Если коэффициент регрессии оказывается больше единицы, то у < С + 1, и на потребление расходуются не только доходы, но и сбережения. Коэффициент регрессии в функции потребления используется для расчета мультипликатора:
Здесь m ≈ 2,86, поэтому дополнительные вложения 1 тыс. руб. на длительный срок приведут при прочих равных условиях к дополнительному доходу 2,86 тыс. руб. При линейной регрессии в качестве показателя тесноты связи выступает линейный коэффициент корреляции r:
Его значения находятся в границах: 0 < r ≤ 1. Если b > 0, то 0 ≤ r ≤ 1, при b< 0, – 1 ≤ r < 0. По данным примера r =0,991, что означает очень тесную зависимость затрат на производство от величины объема выпускаемой продукции. Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации как квадрат линейного коэффициента корреляции r2. Он характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:
Величина 1 - r2 характеризует долю дисперсии у, вызванную влиянием остальных, не учтенных в модели факторов. В примере σ2 = 0,092. Уравнением регрессии объясняется 98,2% дисперсии у, а на прочие факторы приходится 1,8%, это остаточная дисперсия. 1.3. Предпосылки МНК (условия Гаусса-Маркова) Как было сказано выше, связь между у и х в парной регрессии является не функциональной, а корреляционной. Поэтому оценки параметров а и b являются случайными величинами, свойства которых существенно зависят от свойств случайной составляющей
1°. Математическое ожидание случайного отклонения равно нулю для всех наблюдений: 2°. Дисперсия случайных отклонений постоянна: Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсии отклонений) 3°. Случайные отклонения
Выполнимость этого условия называется отсутствием автокорреляции. 4°. Случайное отклонение должно быть независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если объясняющие переменные в данной модели не являются случайными. Кроме того, выполнимость данной предпосылки для эконометрических моделей не столь критична по сравнению с первыми тремя. При выполнимости указанных предпосылок имеет место теорема Гаусса-Маркова: оценки (7) и (8), полученные по МНК, имеют наименьшую дисперсию в классе всех линейных несмешенных оценок Таким образом, при выполнении условий Гаусса-Маркова оценки (7) и (8) являются не только несмещенными оценками коэффициентов регрессии, но и наиболее эффективными, т.е. имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величина. Именно понимание важности условий Гаусса-Маркова отличает компетентного исследователя, использующего регрессионный анализ, от некомпетентного. Если эти условия не выполнены, исследователь должен это сознавать. Если корректирующие действия возможны, то аналитик должен быть в состоянии их выполнить. Если ситуацию исправить невозможно, исследователь должен быть способен оценить, насколько серьезно это может повлиять на результаты. Нелинейная регрессия До сих пор мы рассматривали лишь линейную модель регрессионной зависимости у от х (3). В то же время многие важные связи в экономике являются нелинейными. Примерами такого рода регрессионных моделей являются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства - трудом, капиталом и т.п.) и функции спроса (зависимости между спросом на какой-либо вид товаров или услуг, с одной стороны, и доходом и ценами на этот и другие товары - с другой). При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации. В случае линеаризации нелинейной зависимости получаем линейное регрессионное уравнение типа (3), параметры которого оцениваются обычным МНК, после чего можно записать исходное нелинейное соотношение. Несколько особняком в этом смысле стоит полиномиальная модель произвольной степени:
к которой обычный МНК можно применять без всякой предварительной линеаризации. Рассмотрим указанную процедуру применительно к параболе второй степени:
Такая зависимость целесообразна в случае, если для некоторого интервала значений фактора возрастающая зависимость меняется на убывающую или наоборот. В этом случае можно определить значение фактора, при котором достигается максимальное или минимальное значение результативного признака. Если исходные данные не обнаруживают изменение направленности связи, параметры параболы становятся трудно интерпретируемыми, и форму связи лучше заменить другими нелинейными моделями. Применение МНК для оценки параметров параболы второй степени сводится к дифференцированию суммы квадратов остатков регрессии по каждому из оцениваемых параметров и приравниванию полученных выражений нулю. Получается система нормальных уравнений, число которых равно числу оцениваемых параметров, т.е. трем:
Решать эту систему можно любым способом, в частности, методом определителей. Экстремальное значение функции наблюдается при значении фактора, равном:
Если b>0, с<0, имеет место максимум, т.е. зависимость сначала растет, а затем падает. Такого рода зависимости наблюдаются в экономике труда при изучении заработной платы работников физического труда, когда в роли фактора выступает возраст. При b<0, с>0 парабола имеет минимум, что обычно проявляется в удельных затратах на производство в зависимости от объема выпускаемой продукции. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей. Зависимости гиперболического типа имеют вид:
Примером такой зависимости является кривая Филлипса, констатирующая обратную зависимость процента прироста заработной платы от уровня безработицы. В этом случае значение параметра b будет больше нуля. Другим примером зависимости (37) являются кривые Энгеля, формулирующие следующую закономерность: с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается, а доля доходов, расходуемых на непродовольственные товары, будет возрастать. В этом случае b <0, а результативный признак в (37) показывает долю расходов на непродовольственные товары. Линеаризация уравнения (37) сводится к замене фактора z=1/х, и уравнение регрессии имеет вид (3), в котором вместо фактора х используем фактор z:
К такому же линейному уравнению сводится полулогарифмическая кривая:
которая может быть использована для описания кривых Энгеля. Здесь 1п(х) заменяется на z, и получается уравнение (38). Достаточно широкий класс экономических показателей характеризуется приблизительно постоянным темпом относительного прироста во времени. Этому соответствуют зависимости показательного (экспоненциального) типа, которые записываются в виде:
или в виде
Возможна такая зависимость:
В регрессиях типа (40) - (42) применяется один и тот же способ линеаризации - логарифмирование. Уравнение (40) приводится к виду:
Замена переменной Y = ln у сводит его к линейному виду:
где
который отличается от (43) только видом свободного члена, и линейное уравнение выглядит так: Y=A+bx+E (46) где A= ln a. Параметры А и b получаются обычным МНК, затем параметр а в зависимости (41) получается как антилогарифм А. При логарифмировании (42) получаем линейную зависимость: Y=A+Bx+E (47) где B =ln b, а остальные обозначения те же, что и выше. Здесь также применяется МНК к преобразованным данным, а параметр b для (42) получается как антилогарифм коэффициента В. Широко распространены в практике социально-экономических исследований степенные зависимости. Они используются для построения и анализа производственных функций. В функциях вида:
особенно ценным является то обстоятельство, что параметр b равен коэффициенту эластичности результативного признака по фактору х. Преобразуя (48) путем логарифмирования, получаем линейную регрессию: Y=A+bX+E (49) где Y= ln y, A= ln a, X= ln x, E= ln ε. Еще одним видом нелинейности, приводимым к линейному виду, является обратная зависимость:
Проводя замену и = 1/у, получим:
Наконец, следует отметить зависимость логистического типа:
Графиком функции (52) является так называемая «кривая насыщения», которая имеет две горизонтальные асимптоты у=0 и у=1/а и точку перегиба x= ln (b/a), у=1/(2а), а также точку пересечения с осью ординат у=1/(а+b):
Уравнение (52) приводится к линейному виду заменами переменных и=1/у, z=e-x. Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:
Здесь
Величина R находится в границах 0 ≤ R ≤ 1, и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с линейным коэффициентом корреляции в случае, когда преобразование переменных с целью линеаризации уравнения регрессии не проводится с величинами результативного признака. Так обстоит дело с полулогарифмической и полиномиальной регрессией, а также с равносторонней гиперболой (37). Определив линейный коэффициент корреляции для линеаризованных уравнений, например, н пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и для нелинейной зависимости. Иначе обстоит дело в случае, когда преобразование проводится также с величиной у, например, взятие обратной величины или логарифмирование. Тогда значение R, вычисленное той же функцией ЛИНЕЙН, будет относиться к линеаризованному уравнению регрессии, а не к исходному нелинейному уравнению, и величины разностей под суммами в (54) будут относиться к преобразованным величинам, а не к исходным, что не одно и то же. При этом, как было сказано выше, для расчета R следует воспользоваться выражением (54), вычисленным по исходному нелинейному уравнению. Поскольку в расчете индекса корреляции используется соотношение факторной и общей СКО, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации. Оценка существенности индекса корреляции проводится так же, как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F- критерию Фишера:
где n -число наблюдений, m -число параметров при переменных х. Во всех рассмотренных нами случаях, кроме полиномиальной регрессии, m =1, для полиномов (34) m=k, т.е. степени полинома. Величина т характеризует число степеней свободы для факторной СКО, а (п-т-1) - число степеней свободы для остаточной СКО. Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем больше разница между R2 и r2. Близость этих показателей означает, что усложнять форму уравнения регрессии не следует и можно использовать линейную функцию. Практически, если величина (R2-r2) не превышает 0,1, то линейная зависимость считается оправданной. В противном случае проводится оценка существенности различия показателей детерминации, вычисленных по одним и тем же данным, через t -критерий Стьюдента:
Здесь в знаменателе находится ошибка разности (R2-r2), определяемая по формуле:
Если t >tтабл(α;n-m-1), то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна. В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:
Частные уравнения регрессии На основе уравнения (3) можно найти частные уравнения регрессии:
которые связывают результат с одним из факторов при закреплении других факторов на среднем уровне. Они имеют следующий вид:
Это фактически парные уравнения регрессии, которые можно записать так:
Свободные члены этих выражений легко определяются из следующего равенства:
В отличие от парной регрессии, частные уравнения регрессии характеризуют изолированное влияние фактора на результат, поскольку другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
Предположим, что по ряду регионов регрессионная зависимость величины импорта на определенный товар от отечественного его производства x1, изменения запасов х2 и потребления на внутреннем рынке x3 оказалась следующей:
При этом средние значения составили:
На основе данной информации могут быть найдены средние по совокупности показатели эластичности:
Для данного примераони окажутся равными:
Отсюда видно, что с ростом величины отечественного производства на 1% размер импорта в среднем по совокупности регионов возрастет на 1,053% при неизменных запасах и потреблении. По аналогии интерпретируются и другие показатели эластичности. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. В рассматриваемом примере наибольшее воздействие на величину импорта оказывает размер внутреннего потребления товара х3, а наименьшее изменение запасов х2. В каждом отдельно взятом регионе имеет место своё сочетание значений факторов. Поэтому на основе выражений (18) для каждого региона могут быть определены частные коэффициенты эластичности. Перед этим построим частные уравнения регрессии по каждому фактору:
или конкретно для заданных значений:
Пусть, например, для одного из регионов x1 = 160,2; x2 =4,0, x3= 190,5. Тогда частные коэффициенты эластичности по этому региону составят:
Как видим, частные коэффициенты эластичности для региона несколько отличаются от аналогичных средних показателей по совокупности регионов. Они могут быть использованы при принятии решений относительно развития конкретных регионов. Спецификация модели Все предыдущие рассуждения и выводы, касающиеся классической множественной регрессии, основывались на предположении, что мы имеем дело с правильной спецификацией модели. Под спецификацией модели в данном случае (т.е. для модели линейной множественной регрессии при выполнении предпосылок МНК) будем понимать выбор объясняющих переменных. В этой связи важное значение приобретает рассмотрение двух вопросов, имеющих смысл именно во множественной регрессии, когда исследователь имеет дело с несколькими факторами: возможная мультиколлинеарность факторов и частная корреляция. Последняя особенно тесно связана с процедурами множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.195 (0.171 с.) |
 , (1)
, (1) . (2)
. (2) .
. ,
,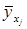 - значение признака, найденное из математической функции связи у и х, т.е. из уравнения регрессии;
- значение признака, найденное из математической функции связи у и х, т.е. из уравнения регрессии;  – случайная величина, характеризующая отклонение реального значения признака от найденного по уравнению регрессии.
– случайная величина, характеризующая отклонение реального значения признака от найденного по уравнению регрессии.
 , отвечающее значению, рассчитанному по уравнению регрессии.
, отвечающее значению, рассчитанному по уравнению регрессии. ,
, ,
, 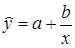 ,
,  .
.
 ;
;  ;
;  ;
;  ;
; 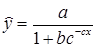 ;
;  .
.

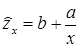




 , где
, где  ,
, 


 , то уравнение регрессии составит
, то уравнение регрессии составит  . Это уравнение можно и не определять, поскольку оно выводится из функции потребления. Коэффициенты регрессии этих двух уравнений связаны равенством:
. Это уравнение можно и не определять, поскольку оно выводится из функции потребления. Коэффициенты регрессии этих двух уравнений связаны равенством: .
. (11)
(11)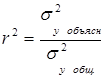 12
12 . Для получения по МНК наилучших результатов необходимо выполнение следующих предпосылок относительно случайного отклонения (условия Гаусса-Маркова):
. Для получения по МНК наилучших результатов необходимо выполнение следующих предпосылок относительно случайного отклонения (условия Гаусса-Маркова):
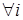 .
. ,
, 
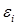 и
и  :
:

 (34)
(34) (35)
(35) (36)
(36) .
. (37)
(37) (38)
(38) (39)
(39) (40)
(40) (41)
(41) (42)
(42)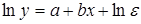 (43)
(43) (44)
(44) . Если Е удовлетворяет условиям Гаусса-Маркова, параметры уравнения (40) оцениваются по МНК из уравнения (44). Уравнение (41) приводится к виду:
. Если Е удовлетворяет условиям Гаусса-Маркова, параметры уравнения (40) оцениваются по МНК из уравнения (44). Уравнение (41) приводится к виду: (45)
(45) (48)
(48) (50)
(50) (51)
(51) (52)
(52)
 (53)
(53) - общая дисперсия результативного признака у,
- общая дисперсия результативного признака у,  остаточная дисперсия, определяемая по уравнению нелинейной регрессии
остаточная дисперсия, определяемая по уравнению нелинейной регрессии  . Следует обратить внимание на то, что разности в соответствующих суммах
. Следует обратить внимание на то, что разности в соответствующих суммах  и
и  берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. По-другому (53) можно записать так:
берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. По-другому (53) можно записать так: (54)
(54) (55)
(55) (56)
(56) (57)
(57)





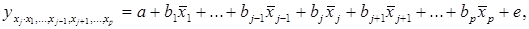



 ,
,  (18)
(18)


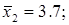

 (19)
(19)














