
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел IV. Электромагнетизм. ⇐ ПредыдущаяСтр 2 из 2
Основные формулы 1. Связь магнитной индукции В с напряженностью Н магнитного поля: где m — магнитная проницаемость изотропной среды; m0 —магнитная постоянная, (m0 =4×p×10-7 Гн/м). В вакууме m =l и тогда магнитная индукция в вакууме: 2. Закон Био -Савара -Лапласа: где dB — магнитная индукция поля, создаваемого элементом проводника длиной dl с током I; `r — радиус-вектор, направленный от элемента проводника к точке, в которой магнитная индукция вычисляется; a — угол между радиусом-вектором и направлением тока в элементе проводника. 3. Магнитная индукция в центре кругового тока: где R -радиус кругового витка. 4. Магнитная индукция на оси кругового тока:
5. Магнитная индукция поля прямого тока:
где r 0 — расстояние от оси проводника до точки, в которой вычисляется магнитная индукция. 6. Магнитная индукция поля, создаваемого отрезком провода с током (рис. 4.1, а):
Обозначения ясны из рисунка. Направление вектора магнитной индукции В обозначено точкой — это значит, что В направлен перпендикулярно плоскости чертежа к нам. При симметричном расположении конца провода относительно точки, в которой определяется магнитная индукция (рис. 4.1,б): cos a 1=cos a 2=cos a, тогда 7. Магнитная индукция в центре дуги окружности длиной L, обтекаемой током I:
8. Магнитная индукция поля соленоида: 9. Сила, действующая на проводник с током в магнитном поле, закон Ампера:
где l — длина проводника; a — угол между направлением тока в проводнике и вектором магнитной индукции В. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности: 10. Сила взаимодействия параллельных проводов с током: где d — расстояние между проводами. 11. Магнитный момент контура с током: где I — сила тока, протекающего по контуру; S — площадь контура; вектор `S численно равен площади S контура и совпадает по направлению с вектором нормали к плоскости контура. 12. Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
где a — угол между векторами ` рт и ` В. 13. Потенциальная энергия; контура с током в магнитном поле:
За нулевое значение потенциальной энергии контура с током в магнитном поле принято расположение контура, когда вектор ` рт перпендикулярен вектору ` В. 14. Отношение магнитного момента ` рт к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите: где Q — заряд частицы; т — масса частицы. 15. Сила Лоренца: где ` V -скорость заряженной частицы; a — угол между векторами ` V и ` В. (Если частица находится одновременно в электрическом и в магнитном полях, то под силой Лоренца понимают выражение 16. Магнитный поток: а) в случае однородного магнитного поля и плоской поверхности Ф = B × S cos a, или Ф = В × S, где S — площадь контура; a — угол между нормалью к плоскости контура и вектором магнитной индукции; б) в случае неоднородного поля и произвольной поверхности: интегрирование ведется по всей поверхности. 17. Потокосцепление (полный поток): Y = N×Ф Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков. 18. Работа по перемещению замкнутого контура в магнитной поле: А = I× D Ф. 19. Э.д.с. индукции (Закон Фарадея): ei = 20. Разность потенциалов на концах проводника, движущегося со скоростью V в магнитном поле: U = B×l×V× sin a, где l -длина проводника; a – угол между векторами V и В. 21. Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур: где r — сопротивление контура. 22. Индуктивность контура: 23. Э.д.с. самоиндукции: es = 24. Индуктивность соленоида: L= где п= 25. Мгновенное значение силы тока в цепи, обладающей сопротивлением r и индуктивностью L: а) при замыкании цепи: где e -э.д.с. источника тока; t -время, прошедшее после замыкания цепи; б) при размыкании цепи: где I 0 — значение силы тока в цепи при t =0; t –время, прошедшее с момента размыкания цепи.
26. Энергия магнитного поля: 27. Объемная плотность энергии магнитного поля (энергия, заключенная в единице объема): где В — магнитная индукция; Н — напряженность магнитного поля.
Методические указания. 1. Основной характеристикой магнитного поля служит вектор магнитной индукции ` В. Задачи на расчет магнитной индукции ` В при заданном распределении токов, создающих магнитное поле, решают с помощью закона Био-Савара-Лапласа и принципа суперпозиции полей. В силу этого принципа магнитная индукция ` В в любой точке магнитного поля проводника с током равна векторной сумме магнитных индукций `dB, созданных в этой точке всеми элементами dl проводника с током: Если магнитное поле создано несколькими проводниками с током, то вектор ` В в какой- либо точке поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности, т.е.: 2. Если требуется определить силу, с которой заданное магнитное поле действует на проводник с током, то сначала находят силу d`F, действующую на произвольный элемент dl длины проводника (силу Ампера), а затем интегрируют полученное выражение по всей длине проводника, учитывая направление складываемых векторов d`F. 3. В явлениях электромагнитной индукции магнитный поток сквозь контур может изменяться как при движении контура или отдельных его участков, так и при изменении во времени магнитного поля. В обоих случаях для определения э.д.с. индукции пользуются законом Фарадея. 4. Если в задаче требуется найти разность потенциалов на концах проводника, движущегося в магнитном поле, то надо иметь в виду, что искомая разность потенциалов численно равна э.д.с., индуцируемой в проводнике. 5. Задачи на движение заряженных частиц в электрическом и магнитном полях по существу решаются методами рассмотренными в механике. Различие лишь в природе сил, действующих на частицу: заряженные частицы движутся лишь под действием силы ` F, состоящей из двух частей: электрической силы Для решения таких задач, как правило, необходимо записать уравнение движения частицы- второй закон Ньютона. Чтобы перейти от векторной записи второго закона к скалярной, надо определить направления векторов ` F эл и ` F м. Магнитная сила всегда перпендикулярна векторам ` V и ` В, поэтому она сообщает движущейся заряженной частице только нормальное ускорение, не изменяя её скорости, и следовательно, не совершая работы. Наоборот, сила ` F эл при перемещении частицы всегда (за исключением случаев, когда `V ^` E) совершает работу, равную изменению кинетической энергии частицы Примеры решения задач. Пример 1. В вершинах квадрата расположены равные положительные заряды- Q = +2×10-7 Кл (рис. 1). В центре квадрата помещен отрицательный заряд. Определить числовое значение этого заряда, если он уравновешивает силы взаимного отталкивания зарядов, расположенных в вершинах квадрата. Дано: q 1= q 2= q 3= q 4=2×10-7 Кл. Найти: q 5.
Силы, которые действуют на заряд q 1 со стороны зарядов q 2, q 3, q 4 и q 5, обозначим F 12, F 13, F 14, и F 15 соответственно. Для равновесия заряда q 1 надо, чтобы векторная сумма этих сил была бы равна нулю: ` F l2 +` F l3 + ` F 14 + ` F 15 = 0. (1) Переходим от векторного выражения к скалярному, проектируя все силы на направление диагонали квадрата, проходящей через заряды q 1: F l2×cos a + F l3 + F 14×cos a - F 15 = 0. (2) где a =45°. Подставляем в уравнение (2) выражение каждой силы из закона Кулона. С учетом того, что q 1= q 2= q 3= q 4= q, r l2 = r l4 = r 23 = r 34= r, F l2 = F 14, можно записать:
По условию: Подставляя выражение (4) в (3), получим окончательно: Подставляя в формулу (5) значения входящих величин, определяем искомый заряд:
Пример 2. По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью t = 10 нКл/м. Определить напряженность Е и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина нити составляет одну треть длины окружности и равна l =15 см. Дано: t = 10 нКл/м, l =15 см. Найти: E, j Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось у была бы симметрично расположена относительно концов дуги (рис 2). На нити выделим элемент длины dl. Заряд dQ = t×dl, находящийся на выделенном участке, можно считать точечным. Определим напряженность электрического поля в точке 0. Для этого найдем сначала напряженность dE поля, создаваемого зарядом dQ:
где ` r — радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность
где `i и ` j -единичные векторы направлений (орты). Напряженность ` Е найдем интегрированием: Интегрирование ведется вдоль дуги длины l. В силу симметрии интеграл
Так как r = R =const, dl = R × dj то dE y = Подставим найденное значение dEy в выражение (1) и, приняв во внимание симметричное расположение дуги относительно оси у, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:
Подставив указанные пределы и выразив R через длину дуги (3 l = 2p R), получим
Из этой формулы видно, что вектор ` Е совпадает с положительным направлением оси у.
Подставим значения t и l в полученную формулу и произведем вычисления:
Найдем потенциал электрического поля в точке 0. Сначала найдем потенциал dj, создаваемый точечным зарядом dQ в точке 0: Заменим r на R и произведем интегрирование: Так как l = 2p× R /3, то Пример 3. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии a = 10 см от ближайшего конца находится точечный заряд Q 1 =40 нКл, который взаимодействует со стержнем с силой F =6 мкН. Определить линейную плотность t заряда на стержне. Дано: l = 20 см =0,2 м; Q 1 =40 нКл =40×10-9 Кл, F =6 мкН=6×10-6 Н. Найти: t.
Интегрируя это выражение в пределах от а до а + l, получим:
откуда интересующая нас линейная плотность заряда: Подставим числовые значения величин в полученную формулу и произведем вычисления: Пример 4. Точечный заряд Q =25 мКл находит в поле созданном прямым бесконечным цилиндром радиуса R =1 см равномерно заряженным с поверхностной плотностью s =0,2 нКл/см2. Определить силу F, действующую на заряд, если его расстояние от оси цилиндра r= 10 см. Дано: s =0.2 нКл/см2=2×10-6 Кл/м2; Q =25 мКл =2,5×10-8 Кл; R =1 см= 0,01 м; r =10 см=0,1 м. Найти: F. Решение. Численное значение силы F, действующей на точечный заряд Q, находящийся в поле, определяется по формуле: F=Q×E (1), где E –напряженность поля. Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра где t -линейная плотность заряда. Выразим линейную плотность t через поверхностную плотность s. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд Q двумя способами: Q = s×S = s× 2×p× R × l и Q = t×l. Приравняв правые части этих равенств и сократив на l, получим: t = 2×p× R×s С учетом этого формула (2) примет вид: Подставив это выражение в (1), получим искомую силу F: Подставим в (3) числовые значения величин: Направление силы ` F совпадает с направлением напряженности `E, а последняя в силу симметрии (цилиндр бесконечно длинный) направлена перпендикулярно поверхности цилиндра. Пример 5. Точечный заряд q =10-8 Кл находится на расстоянии r 1=0,5 м от бесконечно протяженной плоскости, равномерно заряженной с поверхностной плотностью заряда s =4×10-6 Кл/м2. Какую работу надо совершить, чтобы сблизить их до расстояния r 2=0,2 м. Дано: s =4×10-6 Кл/м2; q =10-8 Кл; r 1 = 0,5 м; r 2=0,2 м. Найти: А. Решение. Предположим, что плоскость неподвижна, а точечный заряд q перемещается в электростатическом поле, созданном равномерно заряженной плоскостью.
Работа сил электрического поля определяется формулой А = q (j 2 - j 1), где j 1 и j 2 - соответственно потенциалы электрического поля, созданного бесконечно протяженной заряженной плоскостью в точках 1 и 2. В нашем случае поле плоскости однородное. Потенциал однородного электрического поля с напряженностью Е определяется по формуле j = - Е × r. Здесь r -расстояние от рассматриваемой точки поля до плоскости; Е = s /(2 e о× e), где s - поверхностная плотность заряда на плоскости; e о=8,85×10-12 Ф/м, тогда:
Подставляя в формулу (1) значения входящих величин, определяем искомую величину:
Пример 6. На пластинах плоского конденсатора находится заряд Q = 10 нКл. Площадь S каждой пластины конденсатора равна 100 см2, диэлектрик—воздух. Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным. Дано: S =100 cм2=10-4 м2; Q =10 нКл =10-8 Кл; Найти: F.
Решение. Заряд Q одной пластины находится в поле напряженностью Е, созданном зарядом другой пластин конденсатора. Следовательно, на первый заряд действует сила (рис 4): F=Q×E 1. (1) Так как где s -поверхностная плотность заряда пластины, то формула (1) с учетом выражения (2) примет вид: Подставив числовые значения величин в формулу (3), получим:
Пример 7. Внутри плоского конденсатора с площадью пластин S= 400 см2 и расстоянием между ними d 1 = 5 мм находится пластинка из стекла, целиком заполняющая пространство между пластинами. Конденсатор зарядили до разности потенциалов U= 200 В и отключили от источника напряжения. Какую работу надо совершить, чтобы раздвинуть пластины конденсатора до расстояния d =1,5 см? Дано: S =400 см2=4×10-2 м2; d 1=5 мм=5×10-3 м; U =200 В; d =l,5 см= 0,015 м. Найти: А.
Энергия заряженного конденсатора до раздвижения пластин Здесь U 1- разность потенциалов на обкладках конденсатора; С 1= Энергия поля конденсатора после раздвижения пластин Определим С 2 и U 2. После раздвижения пластин (рис 5,б) на расстояние d получился слоистый конденсатор. Одна часть пространства заполнена стеклом, а другая воздухом (e 2=1). Толщина воздушной прослойки d 2= d –d 1. Емкость такого конденсатора можно определить по формуле двух последовательно соединенных конденсаторов: Тогда Напряжение U 2 найдем из условия постоянства заряда на конденсаторе (q 1= q 2): U 1× C 1= U 2× C 2. Следовательно: Подставив в формулу для W 2 выражения (1) и (2), получим:
Работа по раздвижению пластин равна: A=W 2 – W 1= Тогда A=W 2 – W 1= Пример 8. Сила тока в проводнике сопротивлением r = 20 Ом нарастает в течение времени D t =2 с по линейному закону от I 0=0 до I= 6 A. Определить теплоту Q 1, выделившуюся в этом проводнике за первую секунду, и Q 2 — за вторую, а также найти отношение Q 2/ Q 1. Дано: r = 20 Ом, D t =2 с, I 0=0, I= 6 A. Найти: Q 1, Q 2, Q 2/ Q 1. Решение. Закон Джоуля-Ленца в виде Q = I 2× r×t справедлив для случая постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде: dQ = I 2× r×dt Здесь сила тока I является некоторой функцией времени. В нашем случае I = k×t, (2) где k — коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т. е. С учетом (2) формула (1) примет вид: dQ = k 2× r×t 2× dt (3) Для определения теплоты, выделившейся за конечный промежуток времени D t, выражение (3) надо проинтегрировать в пределах от t 1 до t 2:
При определении теплоты, выделившейся за первую секунду, пределы интегрирования t 1= 0, t 2= 1 с и, следовательно, При определении теплоты Q 2 пределы интегрирования t 1 = 1 с, t 2 = 2 с, тогда
Следовательно, Q 2/ Q 1 = 420/60 = 7, т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую. Пример 9. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра (рис. 6). В этой цепи r 1=100 Ом, r 2 = 50 Ом, r 3 = 20 Ом, э.д.с. элемента e 1 = 2 В. Гальванометр регистрирует ток I 3 = 50 мA, идущий в направлении, указанном стрелкой. Определить э.д.с. e 2 второго элемента. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
Найти: e 2. Решение. Выберем направления токов, как они показаны на рис. 7, и условимся обходить контуры по часовой стрелке. По первому закону Кирхгофа для узла F имеем I 1 – I 2 – I 3 = 0. (1) По второму закону Кирхгофа имеем для контура ABCDFA: -I 1× r 1 – I 2 × r 2 = - e 1, или после умножения обеих частей равенства на –1: I 1× r 1 + I 2 × r 2 = e 1 (2) Соответственно, для контура AFGHA: I 1× r 1 + I 3 × r 3 = e 2 (3) После подстановки числовых значений в формулы (1), (2) и (3) числовых значений получим: Перенеся в этих уравнениях неизвестные величины в левые части, а известные — в правые, получим следующую систему уравнений:
Эту систему с тремя неизвестными можно решить обычными приёмами алгебры, но так как по условию задачи требуется определить только одно неизвестное e 2 из трех, то воспользуемся методом определителей. Составим и вычислим определитель D системы:
Составим и вычислим определитель D e 2:
Разделив определитель D e 2 на определитель D, найдем числовое значение э.д.с. e 2: e 2 = -300/-75 = 4 В. Пример 10. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I =60 А, расположены на расстоянии d =10 см друг от друга. Определить магнитную индукцию` В поля, создаваемого проводниками с током в точке А (рис. 7), отстоящей от оси одного проводника на расстоянии r 1=5 см, от другого - r 2= 12см. Дано: I =60 А, d =10 см=0,1 м, r 1=5 см=0,05 м, r 2= 12см=0,12 м. Найти: `В.
Абсолютное значение магнитной индукции В может быть найдено по теореме косинусов: где a -угол между векторами ` В 1 и ` В 2. Значения магнитных индукций В 1 и B 2 выражаются соответственно через силу тока I и расстояния r 1 и r 2 от проводов до точки А: Подставляя выражения В 1 и B 2 в формулу (1) и вынося m 0× I /2p за знак корня, получим
Вычислим cos a. Заметив, что a =ÐDAC (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем d 2= После подстановки числовых значений получим: Подставляя в формулу (2) значения входящих величин, определяем искомую индукцию:
Пример 11. По проводу, согнутому в виде квадрата со стороной а =10 см, течет ток силой I =100 А. Найти магнитную индукцию` В в точке О пересечения диагоналей квадрата. Дано: I =100 А, а =10 см=0,1 м. Найти: `В. Решение. Расположим квадратный виток в плоскости чертежа (рис. 8). Согласно принципу суперпозиции магнитных полей, магнитная индукция` В поля квадратного витка будет равна геометрической сумме магнитных индукций полей, создаваемых каждой стороной квадрата в отдельности:
Кроме того, из соображений симметрии, следует, что абсолютные значения этих векторов одинаковы: В 1= В 2= В 3= В 4. Это позволяет векторное равенство (1) заменить скалярным равенством: В =4 B 1. (2) Магнитная индукция В 1 поля, создаваемого отрезком прямолинейного провода с током, выражается формулой: Учитывая, что a 2=p - a 1 и cos a 2= -cos a 1 (рис. 4.3), формулу (3) можно переписать в виде Подставив это выражение В 1 в формулу (2), найдем: Заметив, что r 0= а /2 и cos a 1= Подставим в эту формулу числовые значения физических величин и произведем вычисления: Пример 12. Плоский квадратный контур со стороной а = 10 см, по которому течет ток силой I =100 А, свободно установился в однородном магнитном поле (В =1Тл). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) j= 90°; 2) j= 3°. При повороте контура сила тока в нем поддерживается неизменной. Дано: I =100 А, а =10 см=0,1 м, В= 1 Тл, 1) j= 90°; 2) j= 3°.. Найти: А Решение. Как известно, на контур с током в магнитном поле действует момент сил (рис. 9): где pт - магнитный момент контура; B -магнитная индукция; j -угол между вектором ` pт, направленным по нормали к контуру, и вектором ` В. По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (M =0), а значит, j =0, т. е. вектора ` pт и` В совпадают по направлению. Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу работы в дифференциальной форме: dA=Mdj. Подставив сюда выражение М по формуле (1) и учтя, что p m= I×S = I×a 2, где I - сила тока в контуре; S = а 2 -площадь контура, получим dA = I × В × а 2×sin j × dj. Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:
Работа при повороте на угол j 1=90°: Выразим числовые значения величин в единицах СИ и подставим в (3): A 1 = 100×1×(0.1)2=1 Дж. Работа при повороте на угол j 2=3°. В этом случае, учитывая, что угол j 2 мал, заменим в выражении (2) sinj2 »j2: Выразим угол j 2 в радианах. После подстановки числовых значений величин в (4) найдем: A= Задачу можно решить и другим способом. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур: A=-I× D Ф = I× (Ф 1 – Ф 2). где Ф 1 -магнитный поток, пронизывающий контур до перемещения; Ф 2 -то же, после перемещения.Если j 1=90°, то Ф 1= B×S, Ф 2=0, Следовательно A = I×B×S = I×B×a 2, что совпадает с полученным выше результатом {3). Пример 13. В однородном магнитном поле (В =0,1 Тл) равномерно с частотой п =10 с-1 вращается рамка, содержащая N =1000 витков, плотно прилегающих друг к другу. Площадь рамки S =150 см2. Определить мгновенное значение э.д.с. индукции ei, соответствующее углу поворота рамки в 30°. Дано: В =0,1 Тл, п =10 с-1, N =1000, S =150 см2=0,15 м2, j=30°. Найти: ei Решение. Мгновенное значение э.д.с. индукции ei определяется основным уравнением электромагнитной индукции Фарадея— Максвелла: ei = где Y -потокосцепление. Потокосцепление Y связано с магнитным потоком Ф и числом N витков, плотно прилегающих друг к другу, соотношением Y=N×Ф. Подставляя выражения Y в формулу (1), получим ei =
где В -магнитная индукция; S -площадь рамки; w -круговая (или циклическая) частота. Подставив в формулу (2) выражение Ф и продифференцировав по времени, найдем мгновенное значение э.д.с. индукции: ei = N×B×S×w× sin wt. (3) Круговая частота w связана с частотой вращения п соотношением: w= 2 p×n. Подставляя значение w в формулу (3), получим ei =2× p×n×N×B×S×w× sin wt. (4) Выразив значения величии, входящих в эту формулу, в единицах СИ, и подставив их в формулу (4), произведем вычисления: ei =2×3.14 × 10×103 × 0.1×1.5×10-2×0.5=47.1 B. Пример 14. Соленоид с сердечником из немагнитного материала содержит N =1200 витков провода, плотно прилегающих друг к другу. При силе тока I =4 А магнитный поток Ф =6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида. Дано: I =4 А, Ф =6 мкВб, N =1200. Найти: L, W
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.6 (0.186 с.) |


 или
или 

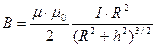
 где h — расстояние от центра витка до точки, в которой вычисляется магнитная индукция.
где h — расстояние от центра витка до точки, в которой вычисляется магнитная индукция.

 .
. 
 , где R -радиус окружности.
, где R -радиус окружности. , где п — число витков соленоида приходящееся на единицу длины.
, где п — число витков соленоида приходящееся на единицу длины. или
или 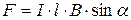


 ,
, или
или 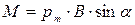
 или
или 

 или
или 
 )
)
 .
. , или
, или 

 .
. = m×m0×n2×V,
= m×m0×n2×V, -число витков, приходящееся на единицу длины соленоида; S- площадь, а V — объем соленоида.
-число витков, приходящееся на единицу длины соленоида; S- площадь, а V — объем соленоида. ,
, ,
, .
. , или
, или  , или
, или  ,
, , где интегрирование проводится по всей длине проводника.
, где интегрирование проводится по всей длине проводника.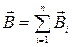 , где n - число проводников с током.
, где n - число проводников с током. и магнитной (лоренцовой силы)
и магнитной (лоренцовой силы)  .
. Решение. Для вычисления q 5 используем закон Кулона и принцип суперпозиции. Заряды q 1, q 2, q 3, и q 4 одинаковы и расположены симметрично. Поэтому рассуждение проводим для одного из четырех зарядов. Определим условие, при котором один из зарядов, например q 1, находился бы в равновесии с зарядом q 5.
Решение. Для вычисления q 5 используем закон Кулона и принцип суперпозиции. Заряды q 1, q 2, q 3, и q 4 одинаковы и расположены симметрично. Поэтому рассуждение проводим для одного из четырех зарядов. Определим условие, при котором один из зарядов, например q 1, находился бы в равновесии с зарядом q 5. 0 (3)
0 (3) . (4)
. (4) . (5).
. (5). Кл.
Кл.
 Выразим вектор dE через проекции dE x и dE y на оси координат:
Выразим вектор dE через проекции dE x и dE y на оси координат: 

 равен пулю. Тогда
равен пулю. Тогда  , где dE y = dE ×cos j=
, где dE y = dE ×cos j= 
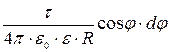 (1)
(1)

 2.18 кВ/м.
2.18 кВ/м.

 . Произведем вычисления:
. Произведем вычисления:  B.
B.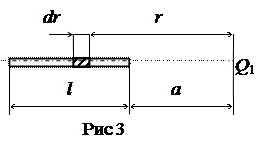 Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Q 1 зависит от линейной плотности t заряда на стержне. Зная эту зависимость, можно определить t. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим на стержне (рис. 3) малый участок dr с зарядом dQ = r×dr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона:
Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Q 1 зависит от линейной плотности t заряда на стержне. Зная эту зависимость, можно определить t. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим на стержне (рис. 3) малый участок dr с зарядом dQ = r×dr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона: 


 Кл/м=2,5 нКл/м.
Кл/м=2,5 нКл/м.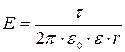 (2)
(2)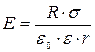
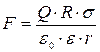 (3)
(3) 565 мкН.
565 мкН. (1)
(1) мДж.
мДж.
 (2)
(2) (3)
(3) мкН.
мкН. Решение. Работа, необходимая для раздвижения пластин, равна изменению энергии конденсатора: A=W 2 – W 1, где W 1 и W 2 - энергия электрического поля конденсатора до и после раздвижения пластин соответственно.
Решение. Работа, необходимая для раздвижения пластин, равна изменению энергии конденсатора: A=W 2 – W 1, где W 1 и W 2 - энергия электрического поля конденсатора до и после раздвижения пластин соответственно. .
. - емкость конденсатора, где d 1- расстояние между пластинами конденсатора, заполненного стеклом с диэлектрической проницаемостью e 1=5 (рис 5, а). Тогда
- емкость конденсатора, где d 1- расстояние между пластинами конденсатора, заполненного стеклом с диэлектрической проницаемостью e 1=5 (рис 5, а). Тогда  .
. .
. , где С 1=
, где С 1=  .
. . (1)
. (1) . (2)
. (2) .
.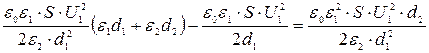 .
. Дж.
Дж. A/c.
A/c. .
. Дж.
Дж. Дж.
Дж. Дано: r 1=100 Ом, r 2 = 50 Ом, r 3 = 20 Ом, e 1 = 2 В, I 3 = 50 мA.
Дано: r 1=100 Ом, r 2 = 50 Ом, r 3 = 20 Ом, e 1 = 2 В, I 3 = 50 мA.



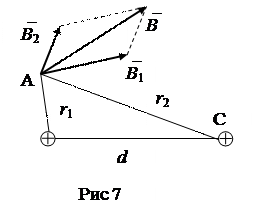 Решение. Для нахождения магнитной индукции` В в точке А воспользуемся принципом суперпозиции магнитных полей; Для этого определим направления магнитной индукции ` В 1 и ` В 2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
Решение. Для нахождения магнитной индукции` В в точке А воспользуемся принципом суперпозиции магнитных полей; Для этого определим направления магнитной индукции ` В 1 и ` В 2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: 
 , (1)
, (1) и
и 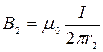 .
. . (2)
. (2) , где d -расстояние между проводами. Отсюда:
, где d -расстояние между проводами. Отсюда:  .
. .
. 3,08×10-4 Тл = 308 мкТл.
3,08×10-4 Тл = 308 мкТл.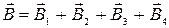 (1)
(1) В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка «к нам».
В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка «к нам». (3)
(3)

 /2 (так как a 1=p/4), получим:
/2 (так как a 1=p/4), получим:  .
. Тл= 1,13мТл.
Тл= 1,13мТл. (1)
(1) (2)
(2) . (3)
. (3) (4)
(4) = 1,37×10-3 Дж = 1,37 мДж.
= 1,37×10-3 Дж = 1,37 мДж. (2)
(2)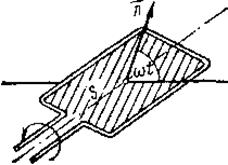 При вращении рамки (рис. 10) магнитный поток Ф, пронизывающий рамку в момент времени t, определяется соотношением Ф = B×S ×cos wt,
При вращении рамки (рис. 10) магнитный поток Ф, пронизывающий рамку в момент времени t, определяется соотношением Ф = B×S ×cos wt,


