
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел III. Электростатика. Постоянный токСтр 1 из 2Следующая ⇒
Основные формулы. 1. Закон Кулона: где F –сила взаимодействия точечных зарядов Q 1 и Q 2, r -расстояние между зарядами; e -диэлектрическая проницаемость; e 0=8,85×10-12 Ф/м –электрическая постоянная. 2. Напряженность электрического поля и потенциал: где П — потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю). 3. Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда: 4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей): 5. Напряженность и потенциал поля, создаваемого точечным зарядом:
6. Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиуса R на расстоянии r от центра сферы: а) если r < R, то Е = 0; б) ecли r = R, то в) ecли r > R, то где Q –заряд сферы. 7. Линейная плотность заряда (заряд, приходящийся на единицу длины заряженного тела): t=Q/l 8. Поверхностная плотность заряда (заряд, приходящийся на единицу площади поверхности заряженного тела): s=Q/S 9. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длины dl с зарядом dQ = t×dl. Такой заряд можно рассматривать как точечный. Напряженность dE и потенциал dj электрического поля, создаваемого зарядом dQ, определяется формулами: где ` r — радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность. Используя принцип суперпозиции электрических полей, находим интегрированием напряженность Е и потенциал j поля, создаваемого распределенным зарядом.
Интегрирование ведется вдоль всей длины заряженной лини. 10. Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром: где r — расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.
11. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью: 12. Напряженность поля между двумя равномерно и разноименно заряженными бесконечными параллельными плоскостями: 13. Связь потенциала с напряженностью: а) в общем случае: ` Е = -grad j, или б) в случае однородного поля: в) в случае поля, обладающего центральной или осевой симметрией: 14. Сила притяжения между двумя разноименными заряженными обкладками конденсатора: 15. Электрический момент диполя: `p=|Q|×`l где Q — заряд; `l -плечо диполя (величина векторная, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами). 16. Работа сил поля по перемещению заряда Q из точки поля с потенциалом j 1 в точку с потенциалом j 2: А 12= Q× (j 1 - j 2) 17. Электроемкость: С = Q / j или С = Q / U, где j – потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U –разность потенциалов пластин конденсатора. 18. Электроемкость уединенной проводящей сферы радиуса R: C= 4× p×e×e 0 ×R 19. Электроемкость плоского конденсатора: 20. Электроемкость слоистого конденсатора:
21. Электроемкость батареи конденсаторов: а) при последовательном соединении: а) при параллельном соединении: где N - число конденсаторов в батарее. 22. Энергия заряженного конденсатора: 23. Сила тока: I=Q / t, где Q –заряд, прошедший через поперечное сечение проводника за время t. 24. Плотность тока: j = I / S, где S –площадь поперечного сечения проводника. 25. Связь плотности тока со средней скоростью < V >- направленного движения заряженных частиц: j=e×n×<V>, где е — заряд частицы; п — концентрация заряженных частиц. 26. Закон Ома: а) для участка цепи, не содержащего э. д. с.: где j 1 - j 2 = U -разность потенциалов (напряжение) на концах участка цепи; r -сопротивление участка; б) для участка цепи, содержащего э. д. с.: где e -э.д.с. источника тока; r –полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в) для замкнутой (полной) цепи: где r –внешнее сопротивление цепи; r 1 –внутреннее сопротивление цепи. 27. Законы Кирхгофа: а) первый закон: где б) второй закон: где 28. Сопротивление r и проводимость G проводника: где r -удельное сопротивление; j – удельная проводимость; l -длина проводника; S - площадь поперечного сечения проводника. 29. Зависимость удельного сопротивления от температуры: rt=r0 × (1+ a×t) 30. Сопротивление системы проводников: а) при последовательном соединении: б) при параллельном соединении: где r i -сопротивление i -го проводника. 31. Работа тока: A=I×U×t=I 2× r×t= Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего э.д.с. 32. Мощность тока: Р=I×U=I 2× r = 33 Закон Джоуля -Ленца: Q= I 2× r×t 34. Закон Ома в дифференциальной форме: j=s×`E где s - удельная проводимость, ` E -напряженность электрического поля, j –плотность тока. 35. Связь удельной проводимости с подвижностью b заряженных частиц (ионов): s=Q×n× (b+ + b-), где Q -заряд иона; п -концентрация ионов; b+ и b- - подвижности положительных и отрицательных ионов. 36. Коэффициент полезного действия источника тока: Методические указания. 1. При решении задач на нахождении напряженности электрического поля могут встретиться следующие случаи: а) поле образовано одним или несколькими точечными зарядами. Тогда используется принцип суперпозиции (наложения) электрических полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, созданных отдельными зарядами; б)поле создано зарядами, которые не являются точечными, но распределены равномерно по сферическим, цилиндрическим или плоским поверхностям. Тогда используют формулы 6,10,11, выведенные с помощью теоремы Гаусса. в) если заряженное тело не является ни сферой, ни бесконечно длинным цилиндром или плоскостью, то для определения напряженности поля необходимо разбить тело на бесконечно малые элементы, найти напряженность d`E поля, созданную в данной точке каждым элементом, а затем просуммировать все элементарные напряженности d`E. 2. Для вычисления потенциала поля, созданного одним или несколькими точечными зарядами, применяют формулу 3. Задача определения емкости конденсатора в общем случае распадается на следующие этапы: а)найти напряженность поля в какой-либо точке пространства между обкладками конденсатора б)найти разность потенциалов на обкладках конденсатора как функцию заряда в)взять величину обратную коэффициенту пропорциональности в полученном выражении, это и будет емкость конденсатора. 4. При расчете электрической цепи, состоящей из конденсаторов, соединенных смешанно (т.е. параллельно и последовательно), поочередно применяя формулу для последовательного и параллельного соединений и переходя от известного к неизвестному, можно найти емкость всего соединения.
5. При расчете электрической цепи, состоящей из конденсаторов и источников постоянного напряжения, которую невозможно разложить на элементы последовательного и параллельного соединений, следует руководствоваться следующими правилами: а)правило узлов, являющееся следствием закона сохранения электрического заряда: если пластины нескольких конденсаторов соединены в один узел, не связанный непосредственно с источником напряжения, то алгебраическая сумма зарядов на этих пластинах равна нулю, т.е. б)правило контуров, вытекающее из закона сохранения энергии: алгебраическая сумма разностей потенциалов на всех конденсаторах и источниках напряжений, встречающихся при обходе любого замкнутого контура, равна нулю, т.е. 6. Для вычисления силы тока и плотности тока, а также расчета сопротивлений при наличии однородных проводников применяют закон Ома в интегральной (при расчете токов в проводниках) или дифференциальной форме (при наличии проводящих безграничных сред) 7. Чтобы безошибочно применять закон Ома для участка цепи, содержащего э.д.с., необходимо придерживаться следующих правил: а)начертить схему и обозначить полюсы всех источников, а также направление тока в цепи 9если оно неизвестно, то надо указать предполагаемое направление); б)ток считать положительным на заданном участке 1-2, если он направлен от точки 1 к точке 2; в)э.д.с. считать положительной на участке 1-2, если она повышает потенциал в направлении от точки 1 к точке 2, т.е. при мысленном движении вдоль пути 1-2 сначала встречается отрицательный полюс источника, а затем положительный. 8. Если требуется рассчитать сопротивление разветвленной цепи, когда заданы сопротивления всех её участков, её надо разложить на участки последовательного и параллельного соединений и, поочередно применяя формулы для последовательного и параллельного соединений проводников, найти сопротивление всей цепи. 9. Для безошибочного применения правил Кирхгофа необходимо выполнять следующие указания: а)выбрать (произвольно) направления токов во всех участках разветвленной цепи, отметив их на чертежах стрелками; б)при составлении уравнений соблюдать правило знаков: токи, притекающие в узел, считать положительными, вытекающие из узла – отрицательными; в)иметь в виду, что число независимых уравнений, составленных по первому правилу Кирхгофа, всегда на единицу меньше числа узлов, имеющих в данной цепи;
г)выбрать направление обхода контуров цепи (по часовой или против часовой стрелке); д)составляя уравнения по второму закону Кирхгофа, соблюдать правило знаков: токи, совпадающие с направлением обхода записывать со знаком «+», обратные направлению обхода – со знаком «–»; считать положительными те э.д.с., которые повышают потенциал в направлении обхода, т.е. двигаясь по контуру, сначала встречаем отрицательный полюс источника, затем положительный; е)чтобы все уравнения, составленные на основании второго правила Кирхгофа были независимыми, необходимо каждый раз рассматривать контуры, содержащие хотя бы одну новую ветвь цепи, не входящую в уже использованные контуры; ж)если в полученном ответе какой-либо ток будет иметь знак «–», то это укажет на ошибочность первоначального выбора направления данного тока, т.е. ток в действительности течет в обратном направлении.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.047 с.) |

 и
и 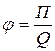
 и П=Q×j
и П=Q×j и
и  ,где E i, (j i — напряженность и потенциал в данной точке поля, создаваемого i -м зарядом).
,где E i, (j i — напряженность и потенциал в данной точке поля, создаваемого i -м зарядом). и
и  , где r — расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
, где r — расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
 ;
; 
 и
и 
 и
и 
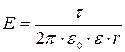






 , где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами.
, где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами. , где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами.
, где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами. ;
; ;
; .
.


 ,
,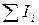 — алгебраическая сумма сил токов, сходящихся в узле;
— алгебраическая сумма сил токов, сходящихся в узле;
 -алгебраическая сумма произведений сил токов на сопротивления участков;
-алгебраическая сумма произведений сил токов на сопротивления участков; 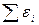 -алгебраическая сумма э.д.с.
-алгебраическая сумма э.д.с. ;
; 






 .
.


