Задача 8 «Пересечение поверхностей вращения»

 

Задание. Построить линию пересечения заданных непрозрачных поверхностей (геометрических тел). Данные к задаче 8 приведены в таблице 6.

Для построения проекций лини пересечения поверхностей вращения часто используют метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей выбирают проецирующие плоскости, перпендикулярные осям тел вращения. Тела вращения на чертеже располагают так, чтобы их основания были параллельны одной из плоскостей проекций. Предложенные варианты заданий содержат два типа задач.

● О дна из поверхностей является проецирующей, т.е. на одну из плоскостей проекций проецируется в линию. К проецирующим относится прямой круговой цилиндр, т.к. его боковая поверхность перпендикулярна основанию и проецируется на одну из плоскостей проекций в окружность. В этом случае одна проекция линии пересечения поверхностей уже построена, и ее изображение совпадает с проекцией цилиндра. Пример решения такой задачи приведен на рисунке 13.

Пусть заданы пересекающиеся поверхности прямого кругового цилиндра и полусферы. Боковая поверхность цилиндра спроецировалась в линию (окружность) на плоскость проекций П₁. Так горизонтальная проекция линии пересечения совпала с горизонтальной проекцией цилиндра. Задача сводится к построению фронтальной проекции линии пересечения. На известной (горизонтальной) проекции линии пересечения определяют положение характерных точек: а и b лежат на основании полусферы, с принадлежит образующей цилиндра, d – образующей конуса (образующие цилиндра и конуса на плоскость проекций П₁ спроецировались в горизонтальную осевую линию).Затем между характерными точками на горизонтальной проекции линии пересечения берут ряд промежуточных точек (для более точного построения проекций линии пересечения берут большее количество точек). Определилась горизонтальная проекция линии пересечения а₁1₁2₁с₁d₁… b₁. Каждая из точек этой линии принадлежит как поверхности цилиндра, так и поверхности полусферы. Фронтальные проекции точек строят, рассматривая точки как принадлежащие полусфере.

Пример построения фронтальных проекций точек приведен на рисунке 13, а. Сначала определяют окружность поверхности полусферы, которой принадлежит точка. Затем проецируют эту окружность на плоскость проекций П₂ – получают отрезок, параллельный проекции основания полусферы. На этот отрезок проецируют точку поверхности сферы. Если одна из пересекающихся поверхностей сфера или часть сферы, то фронтальные проекции точек можно построить другим способом. Пример построения линии пересечения приведен на рисунке 13, б. Через каждую точку мысленно проводят вспомогательную секущую плоскость F, параллельную плоскости проекций П₂. Линия пересечения полусферы с секущей плоскостью F проецируется на плоскость проекций П₁ в часть окружности, на которую затем проецируют точку. На рисунке 14 приведен пример построения проекций промежуточных точек линии пересечения.

а б

Рисунок 13 – Построение проекций линии пересечения

цилиндра и полусферы

 

● Оси пересекающихся поверхностей вращения параллельны, т.е. поверхности являются соосными. Пример решения такой задачи приведен на рисунке 14. При построении линии пересечения двух соосных конусов, большого (с вершиной S и диаметром D) и малого (с вершиной s и диаметром d), вспомогательные секущие плоскости вводят перпендикулярно осям конусов. Секущие плоскости должны быть проецирующими. В результате рассечения обеих поверхностей введенной секущей плоскостью получают линию пересечения, которая на плоскость проекций П₂ проецируется в отрезок, а на плоскость проекций П₁ – в окружности радиусами R (большого конуса) и r (малого конуса). Точки пересечения окружностей, образованных рассечением одной секущей плоскостью, являются точками линии пересечения конусов. Вторую проекцию точки строят, спроецировав ее на отрезок (проекцию линии пересечения) в плоскости П₂. Затем определяют видимость проекций точек. На плоскости проекций П₁ боковая поверхность конусов является видимой, следовательно все геометрические величины (точки, линии), находящиеся на ней, будут видимыми. Чтобы определить видимость на плоскости проекций П₂ смотрят на изображение на плоскости проекций П₁ снизу. Видимой является ближняя по направлению взгляда половина боковой поверхности конуса.

Таким образом, границей видимости является горизонтальная осевая линия проекции конуса. Все геометрические величины, проекции которых находятся в нижней половине горизонтальной проекции конуса (круга), на плоскости проекций П₂ будут видимыми. При определении видимости проекций точек линии пересечения, видимость каждой точки рассматривают относительно обеих поверхностей. Точка является видимой, если она видимая относительно каждой поверхности. Видимость самой линии пересечения определяют по видимости точек, через которые она проводится.

Приступая к решению задачи, сначала определяют характерные точки. Ими являются самые низкие и высокая точки линии пересечения. Проекции низких точек a и b определяют по пересечению проекций оснований большого и малого конусов (окружности диаметрами D и d). Проекции высокой точки с строят на пересечении соответствующих проекций образующих большого (отрезок [S, 2]) и малого (отрезок [s, 3]) конусов. Для построения проекций промежуточных точек секущие плоскости вводят в пределах высокой и низких точек линии пересечения. Для более точного построения линии пересечения строят несколько промежуточных точек, для чего вводят ряд секущих плоскостей. Пример построения проекций промежуточной точки 1 приведен на рисунке 14. Далее определяют видимость точек и строят линию пересечения с учетом видимости.

Приступая к решению задачи 8 анализируют характер заданных поверхностей с целью определения способа решения задачи. Определяют и обозначают латинскими строчными буквами характерные точки линии пересечения поверхностей – высокую и низкие точки. Далее, введя дополнительные секущие плоскости, выполняют построения проекций ряда промежуточных точек, которые обозначают арабскими цифрами. При обводке проекций линии выреза (окна) воспользуйтесь лекалом. Обводку линии производите с учетом видимости. Рекомендуется линию пересечения обводить цветным карандашом.

Рисунок 14 – Построение линии пересечения соосных поверхностей

 

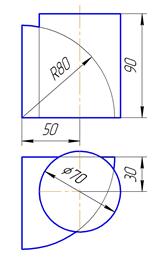
Следы вспомогательных секущих плоскостей следует обозначить, линии построения (сплошные тонкие линии) – сохранить.

Таблица 6 – Данные к задаче 8

Продолжение таблицы 6

Продолжение таблицы 6