Задача 2 «Построение пирамиды»

Задание. Построить фронтальную и горизонтальную проекции пирамиды, основание которой – треугольник АВС, а высота – ребро SА = 60 мм. Координаты вершин треугольников даны в таблице 1.

Вариант

А

В

С

D

Е

F

х

у

z

х

у

z

х

у

z

х

у

z

х

у

z

х

у

z

Таблица 1 - Данные к задачам 1 и 2 (координаты в мм)

 

По условию задачи вершина пирамиды S принадлежит ее высоте и отстоит от вершины основания, точки А, на 60 мм. Высота пирамиды – это перпендикуляр к основанию, опущенный из ее вершины.

Таким образом решение задачи сводится к построению перпендикуляра к плоскости треугольника АВС и определению его натуральной величины.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. Для решения задачи удобно, чтобы этими прямыми были главные линии плоскости.

К главным линиям плоскости относятся линии, принадлежащие заданной плоскости и параллельные одной из основных плоскостей проекций – горизонталь, фронталь и профильная прямая.

По свойству ортогонального проецирования прямой угол проецируется без искажения на ту плоскость проекций, которой параллельна одна из его сторон.

Учитывая свойство ортогонального проецирования прямого угла, одноименные проекции перпендикуляра к плоскости перпендикулярны одноименным проекциям названных выше главных линий плоскости. Т.о. горизонтальная проекция перпендикуляра к плоскости перпендикулярна горизонтальной проекции горизонтали, фронтальная – перпендикулярна фронтальной проекции фронтали.

Горизонталь – прямая, принадлежащая заданной плоскости и параллельная плоскости проекций П₁. Горизонталей в плоскости можно построить множество. Поскольку прямая принадлежит плоскости, если две ее точки принадлежат данной плоскости, то при построении проекций горизонтали, решая данную задачу, можно воспользоваться одной из вершин треугольника АВС. Вторую точку прямой получают на пересечении ее с одной из сторон заданного треугольника.

Решение. По максимальным координатам х, у и zопределяют поле чертежа основания пирамиды – треугольника АВС и размещают в правой части формата А3. Наносят оси координат. По заданным координатам строят проекции вершин треугольника АВС в плоскостях проекций П₁ и П₂.

Пример решения задачи 2 приведен на рисунке 2.

Рисунок 2 – Пример решения задачи 2

В плоскости П₂ строят прямую (А₂, 1₂), фронтальную проекцию горизонтали, параллельно оси Ох. В плоскости П₁ строят горизонтальную проекцию горизонтали – прямую (А₁, 1₁) (по двум точкам). Из вершины А₁ проводят перпендикуляр к прямой (А₁, 1₁). Т.о. будет построена горизонтальная проекция высоты пирамиды.

В плоскости П₁ строят прямую (А₁, 2₁), горизонтальную проекцию фронтали, параллельно оси Ох. В плоскости П₂ строят фронтальную проекцию фронтали – прямую (А₂, 2₂) (по двум точкам). Из вершины А₂ проводят перпендикуляр к прямой (А₂, 2₂). Т.о. будет построена фронтальная проекция высоты пирамиды.

По положению проекций высоты на эпюре определяем, что она занимает в пространстве общее положение и, следовательно, ни на одну плоскость проекций в натуральную величину не проецируется. Отрезок прямой проецируется в натуральную величину только на плоскость, которой он параллелен. Чтобы построить высоту длиной 60 мм (по условию задачи), необходимо ее привести в положение линии уровня, т.е. в положение параллельное одной из плоскостей проекций.

Это действие можно выполнить, решая задачу методом вращения. На горизонтальной проекции высоты берут произвольную точку 3. Прямую (А, 3) поворачивают вокруг оси вращения, проходящую через точку А и перпендикулярную горизонтальной плоскости

проекций, до положения фронтальной прямой (линии, параллельной фронтальной плоскости проекций). При этом на эпюре горизонтальная проекция точки 3 переместиться по окружности в точку 3₁', и горизонтальная проекция высоты займет положение параллельно оси Ох. Фронтальная проекция точки 3 переместится параллельно оси Ох в сторону вращения в точку 3₂'. Прямая (А₂, 3₂') – натуральная величина высоты пирамиды. От точки А₂ по этой прямой откладывают заданную длину высоты и определяют положение точки S₂'. Затем по линиям связи строят проекции вершины S – точки S₂ и S₁.

Далее достраивают боковые ребра и определяют видимость ребер пирамиды методом конкурирующих точек.

 

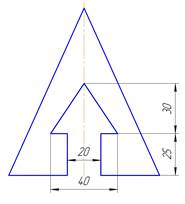
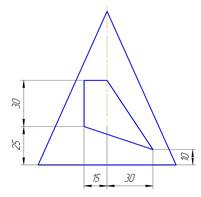
Задача 3 «Двугранный угол»

Задание. Построить фронтальную и горизонтальную проекции двугранного угла, гранями которого являются треугольники АВС и АСD. Определить величину угла при ребре АС. Построить проекции прямой m, удаленной от граней заданного угла на расстояние 15 мм. Координаты вершин треугольников даны в таблице 2.

Чтобы определить натуральную величину двугранного угла необходимо заданный угол привести в положение, при котором грани угла спроецируются в отрезки, при этом общее ребро АС спроецируется в точку. Таким образом решение задачи сводится к приведению ребра АС в проецирующее положение.

Задача решается методом перемены плоскостей проекций. Данный способ решения метрических задач относится к способам преобразования чертежа. Задачи решаются легче, если заданный геометрический объект (отрезок прямой, плоскость) находится в частном положении.

Сущность способа перемены плоскостей проекций заключается в следующем: положение в пространстве заданного геометрического объекта остается неизменным, а заменяют одну или, если необходимо по условию задачи, последовательно две плоскости проекций.

Решение. По максимальным координатам х, у и z определяют поле чертежа треугольников АВС и АСD и размещают в левой верхней части формата А3. Наносят оси координат. По заданным координатам строят проекции вершин треугольников в плоскостях проекций П₁ и П₂.

Пример решения задачи 3 приведен на рисунке 3.

Вводят новую плоскость П₄ перпендикулярно плоскости проекций П₁, и общее ребро АС должно быть параллельно этой плоскости. Образовалась новая система плоскостей проекций П₁ / П₄. Т.о. произошла замена плоскости П₂ на плоскость П₄, на пересечении этих плоскостей проекций образовалась ось Ох ₁. Чтобы построить проекцию вершины треугольника на плоскости П₄, необходимо по линии связи данной вершины, проведенной в новой системе плоскостей проекций, от оси проекций Ох₁ отложить расстояние с замененной плоскости, т.е. расстояние от оси Ох до проекции данной вершиныв плоскости проекций П₂. Спроецировав таким образом на плоскость П₄ двугранный угол, построили натуральную величину общего ребра – отрезок А₄ С₄ (в натуральную величину отрезок прямой проецируется на плоскость, которой он параллелен).

Чтобы привести двугранный угол в проецирующее положение (общее ребро АС спроецировано в точку, а грани угла, заданные треугольники, в отрезки) необходимо произвести вторую перемену плоскостей проекций. Вводят плоскость П₅ перпендикулярно плоскости П₄, и общее ребро АС должно быть перпендикулярно этой плоскости. Образовалась новая система плоскостей проекций П₄ / П₅. Т.о. произошла замена плоскости П₁ на плоскость П₅, на пересечении этих плоскостей проекций образовалась ось Ох ₂. Чтобы построить проекцию вершины треугольника на плоскости П₅, необходимо по линии связи данной вершины, проведенной в новой системе плоскостей проекций, от оси проекций Ох ₂ отложить расстояние с замененной плоскости, т.е. расстояние от оси Ох ₁до проекции данной вершиныв плоскости проекций П₁. Спроецировав таким образом на плоскость П₅ двугранный угол, построили его натуральную величину. Величину двугранного угла АВСD измеряют транспортиром и указывают на эпюре.

Далее по условию задачи необходимо построить проекции прямой m, параллельной общему ребру АС и удаленной от граней угла на 15 мм.

Если прямые параллельны, то их одноименные проекции попарно параллельны.

На плоскость П₅ ребро АС спроецировалось в точку, следовательно, по признаку параллельности прямых, прямая m также спроецируется на эту плоскость проекций в точку.

Строят точку, равноудаленную от сторон угла В₅А₅С₅D₅. Это и будет проекция прямой m₅. Проекцию прямой m₄ строят, проведя в плоскость П₄ линию связи от точки m₅. На прямой m₄ берут произвольную точку N₄ и, путем построения проекций этой точки на плоскостях П₁ и П₂, строят проекции прямой m₁ и m₂. Видимость граней угла и прямой m определяют методом конкурирующих точек.

Рисунок 3 – Пример решения задачи

Таблица 2 – Данные к задачам 3 и 4 (координаты, мм)

Вариант

А

В

С

D

х

у

z

х

у

z

х

у

z

х

у

z

3.4 Задача 4 «Натуральная величина треугольника»

Задание. Определить натуральную величину треугольника АВС. Построить проекции точки К в плоскости треугольника АВС вне его контура на расстоянии n от вершин А и С: n = 0,5 АС + 10 мм. Данные к задаче приведены в таблице 2.

Задачу решают методом плоско-параллельного перемещения. Данный метод решения относится к способам преобразования чертежа. Не изменяя форму и размеры плоской фигуры приводят ее в определенное положение в пространстве путем поворота и перемещения. При этом система плоскостей проекций не изменяется. В натуральную величину плоская фигура проецируется только на параллельную ей плоскость проекций. Такое положение называют положением плоскости уровня.

Плоскостью уровня называют плоскость, параллельную одной из плоскостей проекций. Если заданная плоскость параллельна плоскости проекций П₁, то она является горизонтальной плоскостью, если параллельна П₂, то ее называют фронтальной плоскостью, если параллельна П₃, то ее называют профильной плоскостью.

Т.к. плоская фигура является ограниченной частью плоскости, то все признаки и свойства, относящиеся к плоскости, верны и в отношении и плоской фигуры.

Чтобы фигуру привести в положение плоскости уровня необходимо ее сначала привести в проецирующее положение.

Проецирующей называют плоскость, перпендикулярную одной из основных плоскостей проекций. Если заданная плоскость перпендикулярна плоскости проекций П₁, то она является горизонтально-проецирующей плоскостью, если перпендикулярна П₂, то ее называют фронтально-проецирующей плоскостью, если перпендикулярна П₃, то ее называют профильно-проецирующей плоскостью.

Если заданная плоскость перпендикулярна плоскости проекций, то на эту плоскость она проецируется в прямую линию. Плоская фигура, являясь ограниченной частью плоскости, проецируется на плоскость проекций, которой она перпендикулярна, в отрезок прямой.

Решение. Для решения задачи 4 можно воспользоваться начерченными в задаче 3 проекциями треугольника АВС

Чертеж преобразовывают дважды: сначала треугольник АВС приводят в проецирующее положение, а затем в положение плоскости уровня.

Пример решения задачи 4 приведен на рисунке 4.

Рисунок 4 – Пример построения задачи 4

 

Во фронтально-проецирующее положение треугольник приводят с помощью главной линии плоскости - горизонтали.

Горизонталь – это линия, принадлежащая плоскости и параллельная горизонтальной плоскости проекций. Если треугольник в пространстве расположить так, чтобы горизонталь стала перпендикулярна фронтальной плоскости проекций, то и треугольник будет перпендикулярен этой плоскости проекций.

На эпюре чертят проекции горизонтали (В,1), воспользовавшись одной из вершин треугольника. В плоскости проекций П₂ проекция горизонтали параллельна оси Ох, в плоскости проекций П₁ проекцию горизонтали строят по двум точкам (две точки определяют положение прямой; если точка принадлежит прямой, то проекции точки будут принадлежать одноименным проекциям прямой).

Первый поворот и перемещение треугольника производят таким образом, чтобы горизонталь (В,1) стала перпендикулярна фронтальной плоскости проекций.На эпюре перемещают горизонтальную проекцию треугольника АВС в плоскости П₁, переместив сначала горизонтальную проекцию горизонтали, прямой (В₁,1 ₁) в положение, перпендикулярное оси Ох. Повернутую (не перевернутую) и перемещенную проекцию треугольника А₁'В₁'С₁' дочерчивают с помощью циркуля (форма и размеры треугольника не должны измениться). В плоскости проекций П₂ строят, восстановив линии связи, фронтальную проекцию перемещенного треугольника – отрезок А₂'С₂'.

Второй поворот и перемещение треугольника производят так, чтобы отрезок А₂''С₂'', его фронтальная проекция, стал параллелен оси проекций Ох. Восстановив линии связи, в горизонтальной плоскости проекций строят натуральную величину заданного треугольника. Треугольник А₂''В₂''С₂'' – натуральная величина треугольника АВС.

Измерив длину стороны А₂''С₂'', по формуле, приведенной в задании определяют расстояние от вершин А и С до точки К и строят проекцию точки К₂''. Затем поочередно выстраивают проекции этой точки.

Если точка принадлежит плоскости, то ее проекции принадлежат одноименным проекциям плоскости.

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Прямая принадлежит плоскости, если две ее точки принадлежат этой плоскости.

Задача 5 «Конус с вырезом»

Задание. Построить круговой конус со сквозным поперечным вырезом (окном) призматической формы в трех проекциях. Диаметр основания конуса 90 мм, высота 100 мм. Данные к задаче 5 приведены в таблице 3.

В начертательной геометрии поверхность рассматривают как множество последовательных положений движущейся линии или другой поверхности в пространстве. Линию (поверхность), перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми.

Одна и та же поверхность в ряде случаев может рассматриваться как образованная движением различных образующих.

Образующие поверхность кривые могут быть постоянными и переменными, например закономерно изменяющимися. Образующая поверхности в процессе движения может изменять свою форму и геометрические размеры.

При изображении поверхности на чертеже показывают лишь некоторые из множества положений образующей.

Поверхности можно разбить на классы:

●линейчатые: линейчатые поверхности с одной направляющей (коническая, цилиндрическая, с ребром возврата, торс), линейчатые поверхности с двумя направляющими (цилиндроид, коноид, гиперболический параболоид (косая плоскость), линейчатые поверхности с тремя направляющими (однополостный гиперболоид);

● винтовые: прямая винтовая поверхность (винтовой коноид, прямой геликоид), косая винтовая поверхность (наклонный геликоид);

● циклические: каналовая поверхность, трубчатая поверхность;

● поверхности вращения: цилиндрическая, коническая, сфера, тор.

Поверхность вращения – поверхность, получающаяся при вращении некоторой образующей линии вокруг неподвижной прямой – оси поверхности. На чертежах ось изображают штрихпунктирной линией. Образующая может иметь как кривые, так и прямолинейные участки. Поверхность вращения на чертеже задается образующей и положением оси. При вращении каждая точка образующей описывает окружность в плоскости, перпендикулярной оси. Следовательно, линия пересечения поверхности вращения любой плоскостью, перпендикулярной оси, является окружностью. Такие окружности называются параллелями. Параллель, проходящая через наиболее удаленную от оси точку, называется экватором, через самую близкую точку – горлом. Линия пересечения поверхности вращения плоскостью, проходящей через ось вращения, называется меридианом. Меридиан, лежащий в плоскости, параллельной П₂, называется главным.

Цилиндрическая поверхность образуется вращением прямой (образующей) относительно неподвижной оси, параллельной образующей.

Если цилиндрическую поверхность ограничить двумя плоскостями, то получится круговой цилиндр. Такие плоскости называют основаниями цилиндра. Круговой цилиндр может быть прямой и наклонный. Прямым называют цилиндр, у которого основание перпендикулярно оси вращения. Если поверхность прямого кругового цилиндра на одну из плоскостей проекций проецируется в линию – окружность (когда основание цилиндра параллельно одной из плоскостей проекций), то такую поверхность называют проецирующей. Меридиан прямого кругового цилиндра – прямоугольник). При ортогональном проецировании проекции прямого кругового цилиндра на двух плоскостях проекций – равные прямоугольники (высота равна высоте цилиндра, длина равна диаметру основания цилиндра), на третьей – окружность (диаметр равен диаметру основания конуса).

Коническая поверхность образуется вращением прямой (образующей), закрепленной в некоторой точке на неподвижной оси вращения вокруг этой оси.

Если такую поверхность ограничить плоскостью, перпендикулярной оси, то получится прямой круговой конус. Меридиан прямого кругового конуса – равнобедренный треугольник. При ортогональном проецировании проекции прямого кругового конуса на двух плоскостях проекций – равные равнобедренные треугольники (высота равна высоте конуса, длина основания равна диаметру основания конуса), на третьей – окружность (диаметр равен диаметру основания конуса).

Сфера – ограниченная поверхность вращения. Она образуется вращением окружности (образующей) вокруг неподвижной оси, проходящей через центр окружности. Экватор и меридианы сферы – равные между собой окружности (их диаметр равен диаметру сферы). При ортогональном проецировании на все плоскости проекций сфера проецируется в окружности равного диаметра.

Тор – поверхность, образующаяся при вращении окружности (или ее дуги) вокруг неподвижной оси, лежащей в плоскости окружности, но не проходящей через ее центр. Если ось вращения проходит через образующую-окружность, тор получается самопересекающийся, если касательно к ней – закрытый, если ось вращения находится вне образующей-окружности – открытый (круговое кольцо).

Решение. Круговой конус – поверхность второго порядка. Плоскость, не проходящая через его вершину, пересекает конус по окружности, эллипсу или параболе, если она расположена по одну сторону от вершины, и по гиперболе, если она пересекает его по обе стороны от вершины.

Если секущая плоскость проходит через вершину конуса, то линия пересечения - треугольник. На рисунке 5 изображены проекции линии пересечения с учетом видимости прямого кругового конуса с плоскостью А, проходящей через его вершину.

Рисунок 5 – Построение проекций линии пересечения кругового конуса и

проецирующей плоскости, проходящей через вершину

 

Если секущая плоскость параллельна основанию, то линия пересечения с прямым круговым конусом – окружность. На рисунке 6 изображены проекции линии пересечения с учетом видимости прямого кругового конуса с плоскостью А, перпендикулярной оси.

Рисунок 6 – Построение проекций линии пересечения кругового конуса и

плоскости, перпендикулярной оси

В остальных случаях линией пересечения является кривая линия, построение проекций которой выполняют методом секущих плоскостей по ряду точек. Секущие плоскости являются проецирующими и параллельными основанию конуса. Сначала определяют проекции характерных точек, которые обозначают строчными латинскими буквами (а, b, c), а затем промежуточных, которые обозначают арабскими цифрами.

Точки кривой линии произвольно выбирают на проекции линии пересечения на той плоскости проекций, которой перпендикулярна секущая плоскость (в рассматриваемом случае на П₂), т.к. на нее кривая проецируется в отрезок. Они будут принадлежать фронтальной проекции линии пересечения секущей плоскости и кругового конуса.

Пример построения проекций промежуточной точки 1 приведен на рисунке 7.

Рисунок 7 – Построение эллипса

 

На фронтальной проекции линии пересечения секущей плоскости А и прямого кругового конуса определяют положение промежуточной точки 1. Через нее мысленно проводят вспомогательную секущую плоскость Р (фронтально-проецирующую), параллельную основанию конуса. На чертеже положение секущей плоскости обозначено Р₂1. Эта плоскость рассечет конус по окружности, радиус которой определяют как расстояние от осевой линии конуса до образующей – R1. Точка 1 принадлежит данной окружности. Поэтому для определения горизонтальной проекции точки на плоскости проекций П₁ строят окружность (дугу) радиуса R1 и на нее проецируют точку 1. Поскольку горизонтальная проекция линии пересечения симметрична относительно горизонтальной оси, то проекцию точки 1₁' строят симметрично проекции точки 1₁. Третью проекцию точек строят по двум известным.

Если секущая плоскость, расположена по одну сторону от вершины конической поверхности и пересекает две образующие прямого кругового конуса, линия пересечения – эллипс.

Построения начинают с определения проекций характерных точек. Точки а₂ и с₂ являются точками пересечения проекции секущей плоскости Р₂ и образующими конуса. На горизонтальную плоскость проекций эти образующие проецируются в горизонтальную осевую линию, следовательно точки а₁ и с₁ будут принадлежать этой осевой. На профильную плоскость проекций данные образующие проецируются в вертикальную осевую линию, следовательно точки а₃ и с₃ будут принадлежать данной осевой. Точка b₂ является точкой пересечения проекции секущей плоскости Р₂ и осевой конуса. Горизонтальные проекции точки b определяют методом секущих плоскостей. Профильные проекции этой точкибудут расположены на проекциях образующих.

Затем берут ряд промежуточных точек (более точное построение проекций линии пересечения обеспечивается построением проекций большего числа точек). Проекции промежуточных точек строят методом секущих плоскостей.

Далее определяют видимость проекций линии пересечения. Если рассматривать конус в положении, при котором его основание параллельно горизонтальной плоскости проекций, то боковая поверхность конуса на П ₁ полностью видна, следовательно горизонтальная проекция линии пересечения, принадлежащая поверхности конуса будет видимой. Видимость на фронтальной плоскости проекций определяют, глядя на горизонтальную снизу. Точки, а следовательно и линия, находящиеся на ближней по направлению взгляда половине изображения конуса будут видимыми. Другими словами, все геометрические элементы, находящиеся до осевой линии по направлению взгляда будут видимыми. А точки а ₁ и с₁ являются границей видимости. Определяя видимость на П₃, смотрят на фронтальную проекцию слева. Все геометрические элементы, находящиеся на ближней по направлению взгляда половине поверхности конуса, будут видимыми. Границей видимости является точка b₂, принадлежащая осевой линии. Невидимые контуры линии пересечения на чертеже обводят штриховой линией, обозначение невидимых точек заключают в скобки.

Если секущая плоскость, расположена по одну сторону от вершины конической поверхности и пересекает одну образующую прямого кругового конуса, линия пересечения – парабола. Пример построения параболы приведен на рисунке 8.

Если секущая плоскость, расположена по обе стороны от вершины конической поверхности и пересекает образующие прямого кругового конуса, линия пересечения – гипербола. Проекции точек гиперболы строят методом секущих плоскостей. Видимость определяют по тем же правилам.

Рисунок 8 – Построение параболы

 

Приступая к решению задачи, в левой части листа намечают осевые линии. По заданным размерам чертят три проекции прямого кругового конуса и по заданию своего варианта фронтальную проекцию сквозного выреза (окна). Далее анализируют положение секущих плоскостей, определяющих форму выреза с целью определения вида линий, получающихся при пересечении конуса с этими плоскостями. Определяют и обозначают латинскими строчными буквами характерные точки линий сквозного отверстия: точки концов большой и малой осей эллипсов, точки касания кривых проекций очерков, точки, лежащие на границе видимости. Чтобы построения проекций кривой линии были точнее, ее строят по ряду точек. Поэтому, кроме характерных, выполняют построения промежуточных точек, которые обозначают арабскими цифрами. При обводке проекций линии выреза (окна) воспользуйтесь лекалом. Обводку производите с учетом видимости линий.

Следы вспомогательных секущих плоскостей следует обозначить, линии построения (сплошные тонкие линии) – сохранить.

Таблица 3 – Данные к задаче 5

 

Продолжение таблицы 3

 

Продолжение таблицы 3

 

 

Задача 6 «Сфера с вырезом»