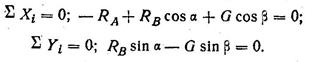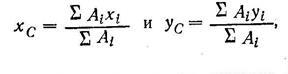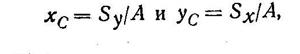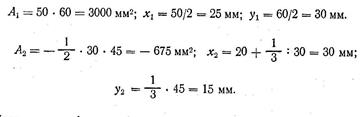Методические указания к выполнению контрольной работы 1

 

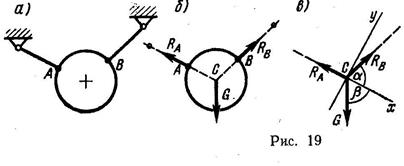
В рекомендованных учебниках [1] или [2], а также в руководствах [3] студенты найдут достаточное число примеров решения задач, подобных тем, которые включены в контрольное задание. Поэтому ниже будут даны лишь необходимые краткие методические указания к решению задач контрольной работы.

Первую задачу контрольной работы (задачи 1—10) следует решить лишь после изучения Введения и тем 1, 2. Все эти задачи (за исключением девятой) сводятся к рассмотрению уравновешенной системы сходящихся сил, располо­женных в одной плоскости. Действительно, если шарообразное тело опирается на две плоскости или удерживается в равновесии плоскостью и нитью либо двумя нитями (рис. 19,а), то на него действует уравновешенная система трех сил: силы тяжести G, приложенной в центре тяжести С тела, и двух реакций нитей векторов Ra и Rb (рис. 19,6), направленных вдоль нитей. В соответствии с теоремой о равновесии трех непараллельных сил, лежащих в одной плоско­сти, ли­нии действия этих сил обязательно пересекутся в одной точке, в' данном слу­чае в точке С — центре тяжести шарообразного тела.

 

Далее можно избрать три способа решения: аналитический, графический и геометрический.

1. При аналитическом способе решения силы векторов Rа и Rb вдоль линий их действия переносим в точку С, т. е. в точку пересечения линий действия трех сил (рис. 19, е) и выбираем оси координат таким образом, чтобы одна из осей (например, ось х) совпадала с направлением какой-либо неизвестной силы. Определив с помощью исходных данных, содержащихся в условии задачи, уг­лы а и р, образуемые с осью х направлением двух других сил, составляем уравнения равновесия и решаем их.

Для системы сил на рис. 19, в уравнения примут вид:

Решив второе уравнение относительно Rb, легко затем из первого урав­нения определить R_A.

2. При решении задачи графическим способом необходимо прежде всего начертить точную схему расположения тела относительно удерживающих его связей, откладывая заданные углы с помощью транспортира.

После этого строится замкнутый силовой треугольник: из произвольной точки С (рис. 19, г) откладывается вертикально вниз в масштабе µсил = G/CD вектор CD, изображающий заданную силу тяжести вектор G; затем через точки С и D проводим прямые, параллельные заданным направлениям искомых сил. Эти прямые пересекутся в некоторой точке Е и в образовавшемся замкнутом треугольнике CDEC сторона вектора DE изображает реакцию вектора R_B, а сторона вектора ЕС — реакцию вектора R_A (R_B = µ_сил · DE; R_A = µ_сил • ЕС).

3. При геометрическом способе решения задачи силовой треугольник CDEC (рис. 19, г) строится в соответствии с исходными данными, но не обязательно в масштабе. Затем, применив теорему синусов:

 

 

 

Вторую задачу контрольной работы (задачи 11—20) следует решить лишь после изучения тем 3 и 4. Во всех этих задачах требуется определить реакции опор балок.

Учащимся необходимо приобрести твердые навыки определения реакций опор, так как с этого начинается решение многих задач по сопротивлению ма­териалов и по деталям машин.

Задачу рекомендуется решать в такой последовательности:

1) изобразить балку вместе с нагрузками на рисунке, соблюдая при эхом заданные размеры ее участков и угла а (эти данные для своего варианта уча-¹ щийся находит в табл. 2);

2) выбрать расположение осей координат (в данном случае целесообразно ось х совместить с балкой, а ось у направить ей перпендикулярно);

3) освободить балку от связей (в точках А и В), заменив эти связи их реакциями; так как направление реакции неподвижного шарнира заранее неиз­вестно, то эту реакцию следует заменить двумя составляющими, направленны­ми вдоль выбранных осей координат, реакция стержня ВС направлена вдоль его собственной оси;

4) составить уравнения равновесия: ∑Xi=0 —алгебраическую сумму проекций на ось х; ∑Ma

(Fi) = 0 — алгебраическую сумму моментов относи­тельно точки A и ∑ Mb(Fi)= 0—алгебраическую сумму моментов относи­тельно точки В;

5) решая систему уравнений, определить значения искомых реакций;

6) обязательно проверить правильность решения задачи, для чего соста­вить уравнение проекций всех сил на ось у (∑Yi=0); если при подстановке числовых значений заданных и найденных величин образуется тождество вида 0=0, то задача решена правильно, если этого тождества не образуется, то надо искать ошибку в решении — проверить правильность составления уравнений и вычислений в ходе их решения.

Третью задачу контрольной работы (задачи 21—30) можно начинать ре­шать после изучения темы 5 и решив несколько задач из рекомендованных •выше. Порядок решения этих задач такой же, как и в предыдущем случае: 1) тело, равновесие которого рассматривается, изобразить на рисунке вместе с действующими нагрузками; 2) выбрать систему осей координат х, у и z; 3) освободить тело от связей, заменяя их действие реакциями; 4) составить шесть уравнений равновесия; 5) решить эти уравнения; 6) проверить правиль­ность решения задачи.

При решении задач на равновесие пространственной системы сил чаще все­го возникают ошибки при составлении уравнений моментов относительно осей Чтобы избежать этих ошибок, целесообразно тело вместе со всеми силами (нагрузками и реакциями связей) спроецировать на три координатные пло­скости. Тогда проще составлять уравнения равновесия. Этот метод подробно описан в руководстве [5], задачи 123-22—126-22.

Четвертую задачу контрольной работы (задачи 31—40) следует решить после изучения темы 6. Во всех этих задачах требуется определить координа­ты центра тяжести однородной пластинки. Навыки определения положения центра тяжести плоских фигур или сечений необходимы для успешного реше­ния многих практических задач в технике.

Положение центра тяжести плоской фигуры определяется по формулам

где х_с и ус — искомые координаты центра тяжести фигуры; xi и y_t — коор­динаты центров тяжести составных частей фигуры, которые определяются непосредственно из заданных размеров; A_t —площади составных частей, кото­рые определяются исходя из тех же размеров.

Иногда приведенным выше формулам придают такой вид:

 

где S_y = ∑Aixi и S_x = ∑Аiyi — статические моменты площади заданной фи­гуры относительно осей у и х соответственно;. А = ∑Ai — площадь заданной

фигуры.

Порядок решения задачи рассмотрим на примере определения положения центра тяжести однородной пластинки, показанной на рис. 20, а (размеры в мм).

 

1. Расположив оси координат, как показано на рис. 20,6, разделим пла­стинки на две части — прямоугольник I со сторонами 50 и 60 мм и вырезан­ный из него прямоугольный треугольник II с катетами 30 и 45 мм.

2. Центр тяжести C1 прямоугольника I лежит на пересечении его диаго­налей (на рис. 20,б они не показаны), а центр тяжести С₂ треугольника II — на пересечении его медиан.

3. Находим площади Аi и координаты x_i и уi центров тяжести частей фигуры:

 

3. Подставляя в формулы приведённые выше значения, находим

1. Расположив оси координат, как показано на рис. 20,6, разделим пла­стинки на две части — прямоугольник I со сторонами 50 и 60 мм и вырезан­ный из него прямоугольный треугольник II с катетами 30 и 45 мм.

2. Центр тяжести С\ прямоугольника I лежит на пересечении его диаго­налей (на рис. 20,6 они не показаны), а центр тяжести С₂ треугольника II — на пересечении его медиан.

3. Находим площади Л₄ и координаты x_t и у г центров тяжести частей фигуры:

 

5. Таким образом, координаты центра тяжести пластинки С (23,5; 34,5).

Метод разделения плоской фигуры, использованный в этом примере, на­зывается методом отрицательных площадей, так как площадям вырезанных частей фигуры приписывается знак минус. В данном случае такой метод по­зволяет разделить фигуру на наименьшее число частей. При использовании только «положительных» площадей заданную пластинку можно разделить не • менее чем на три части (см. рис. 20, в, на котором показан один из двух воз­можных вариантов). Такое разделение несколько удлиняет расчетную часть.

Пятую задачу контрольной работы (задачи 41—50) нужно решать после изучения тем 12 и 13, а также хорошо усвоив Международную систему еди­ниц (СИ). При решении задач следует применять метод кинетостатики. Реко­мендуется такая последовательность: 1) выделить точку, движение которой рассматривается в данной задаче; 2) выяснить, какие активные силы (нагруз­ки) действуют на точку, и изобразить их на рисунке; 3) освободить точку от связей, заменив связи их реакциями; 4) к образовавшейся системе сил доба­вить силу инерции, помня, что направлена она по линии вектора ускорения точки, но в противоположную сторону; 5) выбрать расположение осей коор­динат, составить два уравнения проекций всех сил на оси координат (уравне­ния ∑Xj = 0 и ∑Yi = 0) и, решая эти уравнения, определить требуемые вели­чины.

Если на точку вместе с приложенной силой инерции действуют всего три силы, то задачу можно решить, применив геометрический (графоаналитиче­ский) метод, т. е. построив силовой треугольник.

Шестая задача контрольной работы (задачи 51—60)—это задача на ра­боту и мощность либо при поступательном движении, либо при вращательном движении. Задачу надо решать после изучения тем 14 и 15, повторив мате­риал о трении скольжения и качения. В ходе решения необходимо вниматель­но следить за тем, чтобы числовые значения величин, подставленные в фор­мулы, были выражены в единицах Международной системы (СИ).

В учебниках [1] и [2], а также в руководстве [3] методы решения задач на работу и мощность разобраны достаточно подробно.