
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегралы с бесконечными пределами ⇐ ПредыдущаяСтр 5 из 5
Пусть функция f (x) определена и непрерывна на промежутке [ a;+¥) или (–¥; a ] или (–¥;+¥). Определение 1. Если существует конечный предел Аналогично определяются интегралы:
Если пределы конечные, то соответствующий интеграл считают сходящимся, а если хотя бы один из пределов не существует или бесконечный, то интеграл считают расходящимся.
Интегралы от разрывных функций 1) Пусть функция y = f (x) определена и непрерывна на отрезке [ a; b ], а в точке x = b либо не определена, либо имеет разрыв. Такую точку x = b будем называть особой точкой функции f (x). Определение 2. Если существует конечный предел
Если конечный предел не существует или он бесконечный, то говорят, что несобственный интеграл 2) Пусть функция y = f (x) определена и непрерывна на отрезке [ a; b ], а в точке x = a либо не определена, либо имеет разрыв. Такую точку x = a называют особой точкой функции f (x). Определение 3. Если существует конечный предел При этом говорят, что несобственный интеграл
Если конечный предел не существует или бесконечен, то говорят, что несобственный интеграл Замечание. Если функция f (x) имеет разрыв в некоторой точке x = c внутри отрезка [ a; b ], то по определению полагают:
при условии, что оба предела в правой части существуют, и e иd не зависят друг от друга. Этот интеграл также называют несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом:
Сходимость или расходимость такого интеграла зависит от существования или не существования конечного предела.
Примеры с решениями Пример 1. Исследовать на сходимость несобственный интеграл
Решение.
Так как получили конечное число, то интеграл Ответ: Пример 2. Исследовать на сходимость Решение.
Так как получили конечное число, то Ответ: Пример 3. Исследовать на сходимость Решение.
Так как получили конечное число, то Ответ: Пример 4. Исследовать на сходимость Решение.
Так как получили бесконечность, то Ответ:
Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. Ответы 1.
Учебное издание
РУДАКОВСКАЯ Елена Георгиевна АВЕРИНА Ольга Валентиновна ВОРОНОВ Сергей Мирзоевич СТАРШОВА Татьяна Николаевна ХЛЫНОВА Татьяна Вячеславовна РИГЕР Татьяна Викторовна
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.145 (0.008 с.) |
 , то этот предел называется несобственным интегралом от функции f (x) на бесконечном промежутке [ a;+¥) первого рода, обозначается
, то этот предел называется несобственным интегралом от функции f (x) на бесконечном промежутке [ a;+¥) первого рода, обозначается  и в этом случае считается, что интеграл сходится. Если
и в этом случае считается, что интеграл сходится. Если  не существует или равен ¥, то считается, что интеграл
не существует или равен ¥, то считается, что интеграл  расходится.
расходится.

 , то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом
, то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом  . При этом говорят, что несобственный интеграл
. При этом говорят, что несобственный интеграл  сходится и записывается равенство:
сходится и записывается равенство: .
. , то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом
, то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом  .
. сходится и записывается равенство:
сходится и записывается равенство: .
. расходится.
расходится.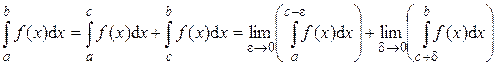
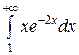

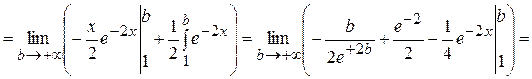

 сходится и равен
сходится и равен  .
. .
.


 сходится и равен –1.
сходится и равен –1.


 сходится и равен
сходится и равен  .
. .
.

 расходится.
расходится. расходится.
расходится. 7.
7. 
 8.
8. 
 9.
9. 
 10.
10. 
 11.
11. 
 12.
12. 
 ; 2. расходится; 3.
; 2. расходится; 3. 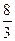 ; 4. расходится; 5. расходится; 6. 6; 7. 1; 8. расходится; 9.
; 4. расходится; 5. расходится; 6. 6; 7. 1; 8. расходится; 9.  ; 10. расходится; 11. 1; 12.
; 10. расходится; 11. 1; 12. 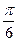 .
.


