
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование тригонометрических выражений
1) Интеграл вида а) Если n – чётное число и m – чётное, то подынтегральное выражение преобразуют с помощью формул:
б) Если одно из чисел m или n – нечётное, то выполняют замену: t = sin x, если n – нечётное; t = cos x, если m – нечётное. Эта замена приводит к интегрированию степенных интегралов или рациональных дробей. в) Если оба числа m и n – нечётные, то интеграл берется как в случае замены: t = sin x, так и t = cos x. 2) Интегралы вида:
где Такие интегралы находят после предварительного применения формул:
3) Интеграл вида: где f (u;v) – рациональная функция двух переменных. Такие интегралы приводятся к интегралам от рациональной дроби с помощью замены:
4) Интегралы вида: где f (u;v) – рациональная функция двух переменных. Такие интегралы находят сведением к интегралу от рациональной дроби с помощью замены:
5) Интегралы вида: Такие интегралы находят после предварительного применения формул:
или с помощью замены:
или Примеры с решениями Пример 1. Вычислить интеграл Решение.
Ответ: Пример 2. Вычислить интеграл Решение.
Ответ: Пример 3. Вычислить интеграл Решение.
Ответ:
Пример 4. Вычислить интеграл Решение.
Ответ: Пример 5. Вычислить интеграл Решение.
Ответ: Пример 6. Вычислить интеграл Решение.
Ответ: Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.
16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Ответы 1. 4.
Интегрирование некоторых видов иррациональных выражений 1) Интеграл вида находят с помощью преобразований и замены, аналогичных преобразованиям и замене для нахождения интеграла от простой рациональной дроби III типа (см. § 5). 2) К интегралам от функций, рационально зависимых от тригонометрических функций, сводятся интегралы:
3) Если подынтегральная функция содержит 4) Интеграл вида Примеры с решениями Пример 1. Вычислить интеграл:
Ответ: Пример 2. Вычислить интеграл:
Ответ: Пример 3. Вычислить интеграл:
Ответ: Пример 4. Вычислить интеграл:
Ответ: Пример 5. Вычислить интеграл:
Ответ: Пример 6. Вычислить интеграл: Ответ: Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Ответы
Определённый интеграл Пусть на отрезке [ a;b ] задана непрерывная неотрицательная функция y = f (x) (рисунок).
Определение 1. Сумма Определение 2. Предел интегральных сумм
При этом отрезок [ a;b ] называют отрезком интегрирования, «a»–нижним пределом интегрирования,«b»–верхним пределом. Достаточное условие интегрируемости функции на отрезке [ a;b ]. Если функция f (x) на отрезке [ a;b ] непрерывна, то определённый интеграл
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.96 (0.03 с.) |


 ,
, 
 ;
; 
 ;
; 




 ,
,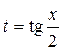 ;
; ;
; ;
;  .
. ,
,
 ;
; 
 ;
;  , где
, где 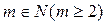 .
. ;
; 
 ;
; .
.












 .
. .
.












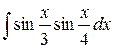














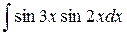








 ; 2.
; 2.  ; 3.
; 3.  ;
;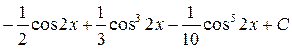 ; 5.
; 5. 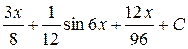 ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  ; 21.
; 21.  ; 22.
; 22.  ; 23.
; 23.  ; 24.
; 24. 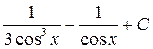 ; 25.
; 25.  ; 26.
; 26. 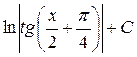 ; 27.
; 27.  ; 28.
; 28.  ; 29.
; 29. 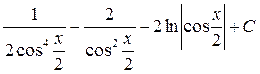 ; 30.
; 30.  .
.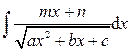
 – подстановкой,
– подстановкой, 

 – подстановкой
– подстановкой 

 – подстановкой
– подстановкой 

 , то надо выполнить замену
, то надо выполнить замену  .
. можно найти подстановкой
можно найти подстановкой 









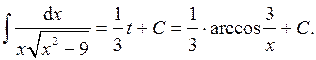










 11.
11. 
 12.
12. 
 13.
13. 
 14.
14. 
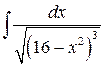 15.
15. 
 16.
16. 
 17.
17. 
 18.
18. 
 19.
19. 
 20.
20. 







 называется интегральной суммой функции f (x) на отрезке [ a;b ].
называется интегральной суммой функции f (x) на отрезке [ a;b ]. функции f (x) на отрезке [ a;b ] при n ® ¥ и max Dxk ® 0 называется определённым интегралом функции f (x) на отрезке [ a;b ], если этот предел существует и не зависит ни от способа разбиения отрезка [ a;b ] на части, ни от выбора точек Mk (k = 1,…, n) на каждой из частей. Следовательно, можно записать:
функции f (x) на отрезке [ a;b ] при n ® ¥ и max Dxk ® 0 называется определённым интегралом функции f (x) на отрезке [ a;b ], если этот предел существует и не зависит ни от способа разбиения отрезка [ a;b ] на части, ни от выбора точек Mk (k = 1,…, n) на каждой из частей. Следовательно, можно записать: .
. существует, т.е. функция f (x) на отрезке [ a;b ] интегрируема.
существует, т.е. функция f (x) на отрезке [ a;b ] интегрируема.


