Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Интегральное исчисление функции одной переменнойСтр 1 из 5Следующая ⇒
ГЛАВА 2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ Первообразная функция и неопределенный интеграл Определения и свойства неопределенного интеграла Определение 1. Функция F (x) называется первообразной для функции f (x) на некотором промежутке, если в каждой точке этого промежутка функция F (x) дифференцируема и выполняется равенство F '(x) = f (x). Если известна одна первообразная F (x) для функции f (x) на интервале (a; b), то любая другая первообразная может быть представлена в виде F (x) + С, где С – произвольная постоянная величина. Такая форма записи первообразных носит название общего вида первообразной. Геометрически, в системе координат xoy, графики всех первообразных функций от данной функции f(x) представляют семейство кривых, зависящих от одного параметра с, которые получаются одна из другой путем параллельного сдвига вдоль оси oy (рис. 1).
Рис. 1. Семейство первообразных функций
Определение 2. Множество всех первообразных для данной функции f (x) на интервале (a; b) называется неопределённым интегралом функции f(x) на этом интервале и обозначается символом:
Теорема 1. Если функция f (x) непрерывна на промежутке (a; b), то она имеет на промежутке (a; b) первообразную и неопределённый интеграл. Из определений первообразной F (x) и неопределённого интеграла от данной функции f (x) на некотором промежутке следуют свойства неопределённого интеграла: 1. 2. 3. 4. 5.
Замечание. Все вышеперечисленные свойства верны при условии, что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.
Таблица основных неопределённых интегралов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. В формулах 1–16 С – произвольная постоянная. Справедливость формул интегрирования, а также и каждый результат интегрирования можно проверить путем дифференцирования на том основании, что интегрирование есть действие обратное дифференцированию.
Примеры с решениями Пример 1.
Пример 2.
Пример 3.
Ответ:
Пример 4.
(формула: – Ответ:
Пример 5.
Ответ: Пример 6.
Ответ: Пример 7.
Ответ:
Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
21.
22.
23. 24. 25. 26.
27.
28.
29.
30.
31. 32. 33. 34.
35.
36.
37. 38. 39. 40. 41. 42. 43. 44. 45. 46.
47.
48.
49.
50. Ответы 1. 37. 40.
Примеры с решениями Пример 1. Найти интеграл Решение.
Ответ: Пример 2. Найти интеграл Решение. Разлагаем подынтегральную функцию на слагаемые, деля числитель почленно на знаменатель.
Ответ: Пример 3. Найти интеграл Решение. Возводим в куб и интегрируем каждое слагаемое.
Ответ: Пример 4. Найти интеграл Решение. Разлагаем подынтегральную дробь на две слагаемых дроби, деля числитель почленно на знаменатель.
Ответ: Пример 5. Найти интеграл Решение. Выделим в неправильной дроби целую часть и правильную дробь.
Ответ: Примеры для самостоятельного решения
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
12. 13. 14. 15. 16. 17. 18. 19. 20.
Ответы 1. 4. 7.
Интегрирование подстановкой Если не удаётся найти интеграл 1) j(t) непрерывна при t Î (a;b), соответствующем интервалу x Î (a; b), 2) дифференцируемая при t Î (a;b); 3) имеет обратную функцию t = j–1(x), чтобы Замечание. Выбор правильной подстановки в значительной степени зависит от искусства вычисляющего. Примеры с решениями Пример 1. Найти интеграл: Решение. Используем формулу
Ответ: Пример 2. Найти интеграл Решение.
Ответ: Пример 3. Найти интеграл Решение.
Ответ: Пример 4. Найти интеграл
Решение.
Ответ: Пример 5. Найти интеграл Решение.
Ответ:
Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
13. 14. 15.
16. 17. 18. 19. 20. 21. 22. 23. 24. Ответы 1.
20.
Интегрирование по частям Метод интегрирования по частям основан на следующей теореме. Теорема 1. Пусть функции u = u (x) и v = v (x) дифференцируемы на некотором интервале (a; b). Пусть на интервале (a; b) функция v (x)× u '(x) имеет первообразную. Тогда на интервале (a; b) функция u (x)× v '(x) также имеет первообразную. При этом справедливо равенство:
Замечание 1. Определение дифференциала и свойства инвариантности его формы позволяют переписать формулу интегрирования по частям в более короткой форме:
Замечание 2. Для успешного вычисления интеграла необходимо разумно разбить подынтегральное выражение на два множителя u (x) и d v (x) так, чтобы интеграл Большая часть интегралов, берущихся с помощью метода интегрирования по частям, может быть разбита на следующие три группы: 1)К первой группе относятся интегралы, у которых подынтегральная функция содержит в качестве множителя одну из следующих функций: ln x; arcsin x; arccos x; arctg x; arcctg x; ln2 x; lnj(x); arcsin2 x;… при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции. Тогда за функцию u (x) берут соответствующую из перечисленных. 2) Ко второй группе относятся интегралы вида:
где a, b, a, n, A – некоторые постоянные числа, A > 0, n Î N. При этом в качестве u (x) следует брать (ax + b) n и интегрировать по частям n раз. 3) К третьей группе относятся интегралы вида:
где a, b, A – постоянные числа, A > 0, A ≠ 1. Такие интегралы берутся двукратным интегрированием по частям при любом выборе u (x). Это приводит к линейному уравнению относительно предложенного интеграла, откуда его и находят.
Примеры с решениями Пример 1. Найти интеграл Решение.
Ответ: Пример 2. Найти интеграл Решение.
Ответ: Пример 3. Найти интеграл Решение.
Ответ: Пример 4. Найти интеграл Решение.
Ответ: Пример 5. Найти интеграл Решение.
Ответ: Пример 6. Найти интеграл Решение.
Далее необходимо решить уравнение:
Ответ:
Пример 7. Найти интеграл Решение.
Пусть
Ответ: Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Ответы 1. 30. Примеры с решениями Пример 1. Найти интеграл Решение. 1) Дробь
Поэтому можно записать:
2) Полученную правильную дробь
Отсюда следует: Значит, подынтегральную рациональную дробь можем представить в виде:
3) Найдём интеграл:
Ответ:
Пример 2. Найти интеграл Решение. 1) Разложим подынтегральную правильную дробь на сумму простых дробей
Отсюда следует:
Найдем интеграл:
Последний интеграл находим по правилу, указанному в интегрировании дроби третьего типа. Выделяем полный квадрат в знаменателе
Подставляя найденный интеграл I в предыдущее выражение искомого интеграла, найдём
Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
12. 13. 14. 15. 16. 17. 18. 19. 20.
Ответы 1.
12. 13. Примеры с решениями Пример 1. Вычислить интеграл Решение.
Ответ: Пример 2. Вычислить интеграл Решение.
Ответ: Пример 3. Вычислить интеграл Решение.
Ответ:
Пример 4. Вычислить интеграл Решение.
Ответ: Пример 5. Вычислить интеграл Решение.
Ответ: Пример 6. Вычислить интеграл Решение.
Ответ: Примеры для самостоятельного решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.
16. 17. 18. 19.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.108.7 (0.375 с.) |



 .
. .
. , где С – произвольная постоянная.
, где С – произвольная постоянная. , где k = const.
, где k = const.
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. (таблица – формула 14)
(таблица – формула 14) (таблица – формула 16)
(таблица – формула 16) (формула: –
(формула: –  ).
). .
.
 ).
). .
. (формула: –
(формула: –  ).
). .
. (формула: –
(формула: –  ).
). .
. (формула: –
(формула: –  ).
). .
.



















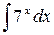




























 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13. 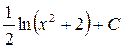 ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  ; 21.
; 21.  ; 22.
; 22.  ; 23.
; 23.  ; 24.
; 24.  ; 25.
; 25.  ; 26.
; 26.  ; 27.
; 27.  ; 28.
; 28.  ; 29.
; 29.  ; 30.
; 30.  ; 31.
; 31.  ; 32.
; 32.  ; 33.
; 33. 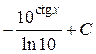 ; 34.
; 34.  ; 35.
; 35. 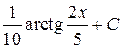 ; 36.
; 36.  ;
; ; 38.
; 38.  ; 39.
; 39.  ;
; ; 41.
; 41.  ; 42.
; 42.  ; 43.
; 43.  ; 44.
; 44.  ; 45.
; 45.  ; 46.
; 46.  ; 47.
; 47. 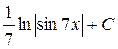 ; 48.
; 48.  ; 49.
; 49.  ; 50.
; 50.  .
.



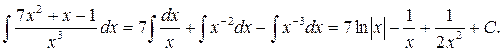
































 ; 2.
; 2.  ; 3.
; 3.  ;
; ; 5.
; 5.  ; 6.
; 6.  ;
; ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  .
. непосредственно, то можно выбрать функцию x = j(t), удовлетворяющую следующим условиям:
непосредственно, то можно выбрать функцию x = j(t), удовлетворяющую следующим условиям: , t = j–1(x) стал табличным или более простым. Иногда для упрощения интеграла можно сделать замену t = y(x).
, t = j–1(x) стал табличным или более простым. Иногда для упрощения интеграла можно сделать замену t = y(x).
 и выделим в знаменателе полный квадрат
и выделим в знаменателе полный квадрат



 .
. .
.

 .
. .
.





















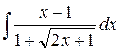







 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14. 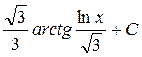 ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18. 
 ; 19.
; 19.  ;
; ; 21.
; 21.  ; 22.
; 22.  ; 23.
; 23.  ; 24.
; 24.  .
. .
. .
. оказался легко интегрируемым.
оказался легко интегрируемым.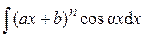 ,
,  ,
, ,
,  ,
, ,
,  ,
,  ,
, ,
,  ,
,  ,
,




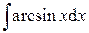















 , тогда уравнение запишется в виде:
, тогда уравнение запишется в виде:

 .
.
 .
.

 .
. , тогда получаем уравнение вида:
, тогда получаем уравнение вида:

 .
. .
.















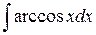












 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  ; 21.
; 21.  ; 22.
; 22. 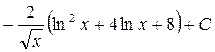 ; 23.
; 23.  ; 24.
; 24.  ; 25.
; 25.  ; 26.
; 26.  ; 27.
; 27.  ; 28.
; 28.  ; 29.
; 29. 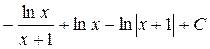 ;
; .
.
 – неправильная рациональная дробь. Выделим её целую часть:
– неправильная рациональная дробь. Выделим её целую часть:
 .
. разложим на сумму простых дробей:
разложим на сумму простых дробей:





 .
. .
.










 и выполняем замену
и выполняем замену  .
.

 .
. .
.



















 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4. 
 ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  8.
8.  ; 9.
; 9. 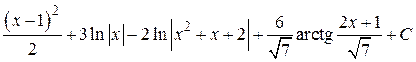 ; 10.
; 10.  ; 11.
; 11.  ;
; ;
;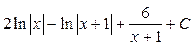 ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19. 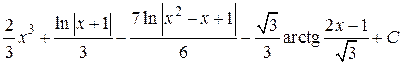 ; 20.
; 20.  .
.












 .
. .
.