
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первичная обработка результатов наблюденийСтр 1 из 17Следующая ⇒
В первичной обработке результатов наблюдений при анализе показателей работы разных отраслей производственной сферы (добыча нефти и газа, ремонт скважин, машиностроение, строительная индустрия и т.д.) и их прогнозировании используют методы математической статистики, которые позволяют установить закономерности производственных результатов с требуемой точностью, надежностью и минимальных материальных, трудовых затратах и оценить их основные свойства. Решение этих вопросов осуществляется методами математической статистики. Основными понятиями математической статистики являются генеральная совокупность и выборка. Генеральная совокупность – это некоторое множество А или совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины. Например, множество всех единиц продукции данного предприятия. Выборка (выборочная совокупность) –случайно выбранное подмножество B Ì A из генеральной совокупности. Например, множество случайно выбранных единиц продукции, при этом некий наблюдатель измерил у них вес в килограммах. Одним из основных методов математической статистики является выборочный метод – метод исследования общих свойств множества А на основе изучения статистических свойств только подмножества В. Число N = | A | элементов множества А называется объемом генеральной совокупности, а число n = | B | - объемом выборки. При изучении некоторого признака Х (в данном примере – веса) выборки производят испытания или наблюдения (измерение веса). Выборку образуют полученные разными способами отбора исходные данные, которые представляют собой множество чисел, расположенных в хаотичном порядке (беспорядке). По такой выборке невозможно выявить определенную закономерность их варьирования (изменчивости). Поэтому с целью обработки исходных данных применяют операцию ранжирования, которая заключается в том, что наблюдаемые значения случайной величины располагают в определенном порядке (возрастания или убывания). После проведения операции ранжирования отдельные значения случайной величины группируют таким образом, чтобы в каждой отдельной группе значения случайной величины были одинаковыми. Каждое из таких значений называется вариантой
Число, которое показывает, сколько раз встречаются соответствующие значение варианты Отношение wi = ni / n частоты ni к объему выборки n называют относительной частотой (частостью) варианты хi. Вариационным рядом (или статистическим распределением) называют последовательность вариантов, записанных в возрастающем порядке и соответствующих им частот или относительных частот. Различают дискретные и непрерывные вариационные ряды. Дискретным статистическим рядом принято называть ранжированную совокупность вариант Принято записывать дискретный статистический ряд в виде табл.1.1.
Таблица 1.1
В случае, когда исследуемая случайная величина Интервальный вариационный ряд, формируется на основании следующего алгоритма: 1. Вычисляют размах R варьирования признака Х, как разность между наибольшим
2. Размах R варьирования признака Х делится на k равных частей и таким образом определяется число столбцов (интервалов) в таблице. Число k частичных интервалов выбирают, пользуясь одним из следующих правил:
При небольшом объеме n выборки число k интервалов принимают равным от 6 до 10. 3. По формуле (1.3) рассчитывают длину частичного интервала
где k – число интервалов.
Величину h обычно округляют до некоторого значения d. Так, если результаты 4. Подсчитывается частота ni, с которой попадают значения Изучая полученные результаты наблюдений, выявляют, сколько значений случайной величины отнесено в каждый конкретный интервал. В интервал включаются значения, большие или равные нижней границе, а меньшие - верхней границы интервала. В первую строку таблицы статистического ряда распределения вписываются частичные промежутки
В качестве начала первого интервала рекомендуется брать начальную величину, определяемую по формуле:
Конец последнего интервала ряда должен полностью удовлетворять условию:
Промежуточные интервалы обычно получают, прибавляя к верхней границе (концу) предыдущего интервала шаг. Сформированный интервальный вариационный ряд записывают в виде табл. 1.2.
Таблица 1.2
Для расчета статистик (выборочной средней, выборочной дисперсии, асимметрии и эксцесса) переходят от интервального к дискретному вариационному ряду. В данном случае серединное значение
Таблица 1.3
Здесь
Таблица 1.4
Здесь
Для характеристики свойств статистического распределения в математической статистике вводится понятие эмпирической функции распределения. Под эмпирической функцией или функцией распределения выборки понимается функция
где
В случае увеличения объема статистической выборки частость события 1. 2. 3. В теории вероятностей аналогом этой функции является интегральная функция распределения F (x), для которой достоверно приближенное равенство:
где Выборочным тождеством функции
где В случае, если наблюдаемые значения непрерывной случайной величины представлены в виде интервального вариационного ряда, и, предполагая, что wi – это частость попадания данных значений в интервал
где В виду того, что функция
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.251.72 (0.031 с.) |
 .
.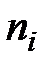 , где
, где 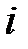 - номер варианты.
- номер варианты.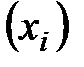 и соответствующих им частот
и соответствующих им частот 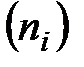 или частостей
или частостей 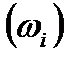 .
.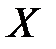 является непрерывной или число ее значений достаточно велико (
является непрерывной или число ее значений достаточно велико ( ), то принято составлять интервальный вариационный ряд.
), то принято составлять интервальный вариационный ряд.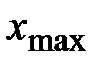 и наименьшим
и наименьшим  значениями признака совокупности:
значениями признака совокупности: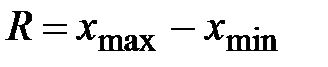 . (1.1)
. (1.1)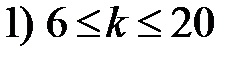 ,
,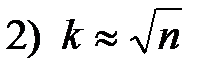 ,(1.2)
,(1.2) .
.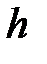 :
: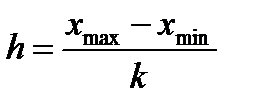 , (1.3)
, (1.3)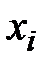 признака Х – целые числа, то h округляют до целого значения, если
признака Х – целые числа, то h округляют до целого значения, если 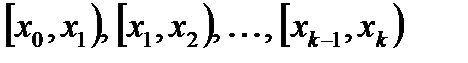 . Во вторую строку – количество наблюдений
. Во вторую строку – количество наблюдений 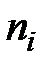 (где
(где 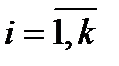 ) попавших в каждый конкретный интервал, т. е. частоты соответствующих интервалов.
) попавших в каждый конкретный интервал, т. е. частоты соответствующих интервалов.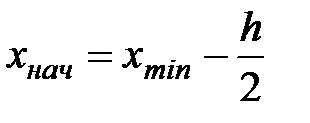 , (1.4)
, (1.4) . (1.5)
. (1.5)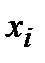 ;
; 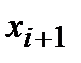 )
)
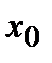 ;
; 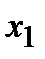 )
)
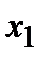 ;
; 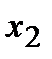 )
)
 ;
; 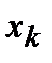 )
)
 -го интервала принимается за варианту
-го интервала принимается за варианту  , а соответствующая интервальная частота
, а соответствующая интервальная частота 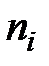 принимается за частоту данного варианта. При этом дискретный вариационный ряд записывается в виде табл. 1.3 или табл. 1.4.
принимается за частоту данного варианта. При этом дискретный вариационный ряд записывается в виде табл. 1.3 или табл. 1.4. , где n - объем выборки.
, где n - объем выборки.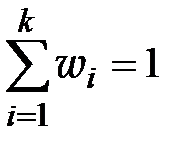 .
.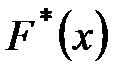 , которая определяет частость события
, которая определяет частость события 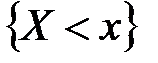 для каждого отдельного значения
для каждого отдельного значения 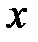 :
: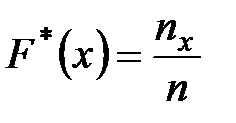 , (1.6)
, (1.6)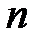 - объем выборки,
- объем выборки,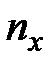 – число наблюдений, меньших
– число наблюдений, меньших 
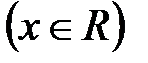 .
.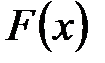 . Стоит отметить, что функции
. Стоит отметить, что функции 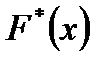 и
и  ;
;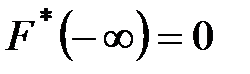 ,
,  .
. , (1.7)
, (1.7)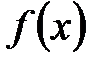 – дифференциальная функция распределения или функция плотности вероятности.
– дифференциальная функция распределения или функция плотности вероятности.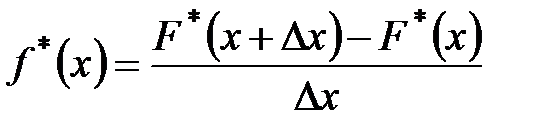 , (1.8)
, (1.8)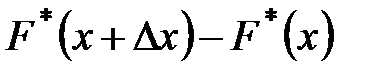 – частость попадания наблюдаемых значений случайной величины
– частость попадания наблюдаемых значений случайной величины 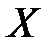 в интервал
в интервал 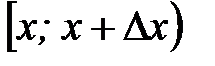 . Следовательно, значение
. Следовательно, значение 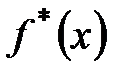 является характеристикой плотности частости на данном интервале.
является характеристикой плотности частости на данном интервале.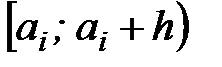 , где
, где 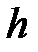 – длина частичного интервала, то выборочная функция плотности
– длина частичного интервала, то выборочная функция плотности 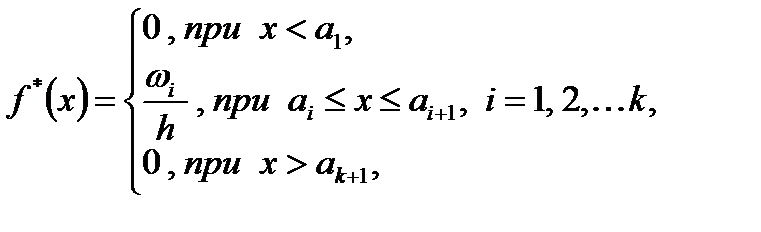 (1.9)
(1.9) – конец последнего k -го интервала ряда.
– конец последнего k -го интервала ряда.


