
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Меры оценки колеблемости ряда и типичности средних величин
Средние арифметические величины, взятые сами по себе без дополнительных приемов оценки, имеют подчас ограниченное значение, т. к. они не отражают степени рассеяния (или колеблемости) ряда. Одинаковые по размеру средние могут быть получены из рядов с различной степенью рассеяния. Средние — это величины, вокруг которых рассеяны различные варианты. Понятно, что чем ближе друг к другу отдельные варианты, (значит меньше рассеяние, колеблемость ряда), тем типичнее его средняя. Примером могут служить две средние, полученные из следующих рядов (табл. 6.3.), составленных на сроках длительности случаев утраты трудоспособности по поводу одного и того же заболевания (числа условные). Таблица 6.3 Пример получения средней величины
Обе средние величины получены правильно (сумма величин, деленная на число наблюдений), но даже «невооруженному глазу» видно, что их ценность, значение, типичность далеко не одинаковы и что вторая средняя не может служить типичной характеристикой ряда, с его резкой колеблемостью. Очевидно, следует прибегнуть к дополнительным мерам оценки, тем более, что не всегда можно видеть сам ряд распределения, потому что в литературных материалах авторы его не приводят, а пользуются только производными величинами. Первоначальный, приближенный метод оценки — это сравнение амплитуды рядов. Амплитуда (разность между наибольшим и наименьшим значением вариант) в первом ряду составляет всего 3, во втором — 16 (т. е. его колеблемость втрое больше). Амплитуда второго ряда более, чем вдвое превышает значение его средней величины М. Однако амплитуда ряда не учитывает промежуточные значения вариант внутри ряда; кроме того, ее размеры связаны не только с колеблемостью, но могут зависеть и от количества наблюдений. Более точно колеблемость ряда измеряется по отклонениям. Отклонения, обозначаемые буквой d (от латинского слова deviatio), вычисляются как разность между каждой вариантой и средней величиной. Алгебраическая сумма положительных и отрицательных отклонений от средней всегда равна нулю, т. к. средняя нивелирует эти отклонения (в нашем примере +2 и –2; +14 и –14). Попробуем сложить абсолютные значения отклонений, игнорируя их знаки, и разделить на число наблюдений. Мы получаем так называемое среднее отклонение (иногда оно называется линейным или арифметическим отклонением). В первом ряду оно относительно невелико (0,8), во втором ряду (5,6) почти достигает размеров самой средней, что разумеется её обесценивает.
Однако пользование средним отклонением основано на игнорировании положительных и отрицательных знаков, на условном допущении. Поэтому основной, наиболее правильной мерой оценки колеблемости ряда является среднее квадратическое отклонение, при котором отклонения возводятся в квадрат, и, следовательно, все они получают положительные знаки. В таблице 6.4. показано вычисление среднего квадратического, или стандартного, отклонения, обозначаемого греческой буквой s (сигма). Сигма первого ряда составила 1,1, сигма второго ряда — 6,2. Таблица 6.4. Вычисление средней арифметической и среднего квадратического отклонения в простом ряду (непосредственное вычисление)
Значение возведения отклонений в квадрат двоякое: во-первых, оно уничтожает ошибку со знаком, во-вторых, уменьшает значение малых отклонений (меньших, чем единица) и увеличивает значение больших, т. е. делает более выпуклой и рельефной картину отклонений. Ход вычисления средней арифметической и среднего квадратического в простом ряду показан в таблице 6.4.
Из таблицы 6.4. видно, что в ряду, где частоты не равны единице, необходимо квадрат каждого отклонения перемножить на соответственную частоту (т. е. на те числа наблюдений, при которых наблюдалось это отклонение).
Таким образом, вычисление среднего квадратического отклонения производится путем проведения шести последовательных действий. Для вычисления сигмы необходимо:
Как видно из приведенных таблиц даже при незначительном числе наблюдений, получение средней арифметической и среднего квадратического отклонения довольно громоздко и требует ряда подсчетов. Ещё больше усложняется работа при большом числе наблюдений. На практике вычисление средних обычно производится с использованием ПЭВМ в рамках эксплуатации программы MS-EXEL. Как уже упоминалось, сигма характеризует колеблемость ряда, степень рассеяния вокруг средней отдельных вариант. При помощи сигмы можно установить степень типичности средней, пределы рассеяния ряда, пределы колебаний вокруг средней отдельных вариант. Чем меньше сигма, тем меньше колеблемость ряда, и тем точнее и типичнее получается вычисленная на этом ряду средняя. Таким образом, при помощи сигмы мы изучаем колеблемость явления. Применение сигмы дает возможность оценки и сравнения колеблемости нескольких рядов распределения, как однотипных, так и различных, а также оценки изолированного единичного ряда и даже отдельных вариант. При оценке однотипных рядов принимаются во внимание абсолютные размеры сигмы. Так, например, при сравнении двух рядов распределения по признаку веса, если средние будут близки по уровню, но сигма в одном ряду будет 5,6 и в другом 2,1, второй ряд будет менее рассеян, и его средняя более типична и достоверна. При оценке колеблемости различных рядов (например, постоянства таких признаков, как вес и рост) непосредственное сравнение размеров сигмы невозможно, т. к. сигма — величина, именованная и выраженная абсолютным числом. При средней величине веса 62,6 с сигмой в 5,6 и средней величине роста 165 с сигмой 6,6 для установления степени относительной колеблемости рядов следует прибегнуть к производной величине, к коэффициенту изменчивости (вариации), обозначаемому буквой V или С. Коэффициент изменчивости получается из процентного отношения сигмы к средней:
Коэффициент изменчивости для веса в нашем примере будет:
Коэффициент изменчивости для роста — соответственно:
Эти цифры можно сравнить и сделать заключение, что в данном примере рост оказался вдвое более устойчивым признаком, чем вес. Этот же метод вычисления коэффициента изменчивости пригоден и для суждения об однотипных рядах, у которых очень разнятся по размеру средние величины, и для оценки изолированного, единичного ряда. Но более полное суждение о степени рассеяния единичного ряда получается путем прибавления к средней одной, двух и трёх сигм. В ряду с распределением, близким к нормальному, в пределах M ± 1s, т. е. средней и одной сигмы (в сторону минуса и плюса), расположено 68,3% всех вариант. В пределах M ± 2s расположено 95,5% всех вариант. В пределах M ± 3s расположено 99,7 % всех вариант. Амплитуду нормального ряда полагают равной трем сигмам в одну и другую сторону.
Требования, предваряющие определение параметров Вариационного ряда. До вычисления средних величин и определения др. параметров вариационных рядов необходимо проверить, соответствует ли анализируемый материал трем обязательным требованиям, нарушение которых так или иначе ведет к ошибкам. Требование первое - качественная однородность единиц, составляющих анализируемую статистическую совокупность. Чтобы сразу стало понятно, о чем идет речь, рассмотрим реальный пример. Пусть требуется установить средний срок нетрудоспособности в группе больных. Формально для этого нужно поделить общее число дней нетрудоспособности на число больных, что и делается на практике безо всяких дополнительных размышлений. Но может случиться так, что упомянутая группа состоит из двух частей: больных гепатитом и больных с острыми респираторными заболеваниями (ОРЗ). Первые в массе своей будут иметь длительные сроки нетрудоспособности, измеряемые десятками дней, а у вторых нетрудоспособность будет ограничена несколькими днями. Формальный подход, безусловно, приведет к получению среднего срока нетрудоспособности. Но этот срок не будет типичен ни для всей группы больных в целом, ни для одной из подгрупп. Ориентироваться на такой показатель, строить какие-то планы тут бессмысленно, ибо не достигнута основная цель расчета средней – выявление обобщающей характеристики статистической совокупности. Приведенный пример подобран специально – чтобы показать необходимость расчета средних величин в качественно однородных совокупностях. И вряд ли требуется кого-то убеждать, что нужно определять отдельно средние сроки нетрудоспособности в каждой подгруппе больных – это естественно и просто соответствует здравому смыслу. Однако в жизни очень часто средние рассчитываются в качественно неоднородных совокупностях. Рассмотрим два достаточно распространенных показателя. Первый – средняя длительность пребывания на койке в многопрофильном стационаре. В больнице несколько отделений (челюстно-лицевая хирургия, оториноларингологическое отделение для детей, аналогичное для взрослых, отделение дневного пребывания и пр.). Средний показатель по учреждению может быть нетипичным для части из них. Тем не менее, в отчетах и при анализе употребляются обобщающие показатели по больнице в целом и много реже – по отделениям или группам пациентов.
Второй показатель – среднее число посещений в поликлинику на одного человека в год. Имеется в виду – на некоего одного усредненного человека. Но при этом теряются различия между молодыми и старыми людьми, хронически больными и здоровыми, имеющими медицинской обслуживание по месту работы и не имеющими. Приведенные и многие другие показатели в обобщающем виде приемлемы при оценке явлений на больших территориях, среди многочисленных контингентов населения. В рамках же отдельного медицинского учреждения они требуют уточнения по группам населения, больных, по подразделениям учреждения и т.п. Требование второе - достаточность наблюдений. Поскольку средние величины призваны обобщать какую-то типичную характеристику совокупности, последняя должна быть достаточной по численности. Методика определения необходимого объема совокупности описана в главе 5. Здесь лишь отметим, что совокупности численностью менее 30 считаются малыми и имеют ряд особенностей, учесть которые трудно. По возможности лучше избегать анализа таких малых групп. Требование третье - учет вида распределения. Прежде, чем говорить об учете вида, нужно разъяснить, что такое распределение. Сделаем это с использованием вариационного ряда и изобразим его графически (рис. 6.4.). Если в системе координат (по горизонтальной оси которой отмечены варианты, а по вертикальной – частоты) отметить точки, соответствующие этому ряду, а затем точки соединить – получится кривая распределения вариант в соответствии с их частотами. Большинство явлений в природе имеют в принципе похожее распределение вариант, названное нормальными. Не вдаваясь в математическое описание нормального распределения отметим, что оно характеризуется колоколообразной формой с постепенным увеличением частот от начала до середины ряда и симметричным сокращением частот от середины к концу ряда.
Рис. 6.4. Кривая нормального распределения Вид (форма) этой кривой будет нас интересовать в связи со следующими положениями.
Рис. 6.5 Рис. 6.6. Особо следует отметить распределения, изображенные на рисунках 6.7 и 6.8. Если кривая образует два и более горба (рис. 8) или «плато» (рис. 9), это, скорее всего, свидетельствует о качественной неоднородности анализируемой совокупности.
Рис. 6.7. Рис. 6.8.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.199.243 (0.04 с.) |
 дней
дней




 =2232
=2232
 =114
=114
 ;
; 


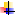 определить отклонения от средней;
определить отклонения от средней; .
. .
. .
.


