
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние величины в медицинской статистике. Оценка физического развития
Основные понятия. В клинической практике и медико-биологических исследованиях, наряду с абсолютными и относительными, широко используются средние величины. К вычислению средней величины в медицинских исследованиях обычно прибегают, когда требуется получить обобщающую характеристику явлений (процессов) по какому-либо количественному признаку. Средняя величина характеризует весь ряд наблюдений одним числом. Она нивелирует, ослабляет случайные отклонения индивидуальных наблюдений в ту или иную сторону и выдвигает на первый план основное, типичное свойство явления. В практической деятельности врача средние величины используются:
Статистические коэффициенты и средние величины представляют собой вероятностные величины, некоторые усредненные результаты. Но между ними существуют значительные различия. Коэффициент характеризует признак, встречающийся только у некоторой части статистического коллектива, — так называемый альтернативный признак, который может иметь или не иметь место (рождение, смерть, заболевание, инвалидность). Средние же величины охватывают признаки, присущие всем членам коллектива, но в разной степени (масса тела, рост, возраст) — этими признаками обладают все исследуемые. Коэффициенты применяются для измерения качественных признаков, а средние величины — для варьирующих количественных признаков. При использовании средних величин речь идет об отличиях в числовых размерах признака, а не о факте его наличия или отсутствия. В лабораторно-экспериментальной практике статистические коэффициенты применяются для характеристики реакций, учитываемых в альтернативной форме («все или ничего»; реакция наступает или не наступает). При учете реакции в количественной градуированной форме — концентрация, дозировка, время — для их обобщения применяются средние величины. Основное достоинство средних величин — их типичность: средняя сразу дает ориентировку, общую характеристику явления. В связи с этим возникают две предпосылки, два условия для вычисления средних: ü средние величины должны быть рассчитаны на основе качественно однородных статистических групп, имеющих существенные общие социально-экономические или биологические характеристики (если изучаемая совокупность качественно неоднородна по составу, то вычисленная на основе ее данных величина не будет правильно отражать типичные, характерные особенности изучаемого явления); ü средние величины должны быть рассчитаны на совокупностях, имеющих достаточно большое число наблюдений; это требование основано на законе больших чисел.
В медико-социальных исследованиях обычно используются 4 вида средних величин: средняя арифметическая (М — Media), мода (Мо), медиана (Mе) и средняя прогрессивная (Мпр). Другие виды средних величин применяются в специальных экспериментальных углубленных исследованиях (рис. 6.1). Так, средняя квадратическая применяется для определения среднего диаметра среза клеток, результата накожных иммунологических проб, для определения средней площади опухолей; средняя кубическая — для определения среднего объема опухолей. Средняя геометрическая применяется при расчетах численности населения в межпереписные годы, при вычислении среднего темпа роста или прироста, при обработке результатов титрования антител, токсинов и вакцин в эксперименте. Средняя гармоническая может применяться при изучении титров лизоцимов, коли-титра и коли-индекса. Чаще всего в санитарной статистике используется средняя арифметическая величина, представляющая собой как бы прототип остальных средних. Средние величины рассчитываются на основании вариационных рядов.
КЛАССИФИКАЦИЯ СРЕДНИХ ВЕЛИЧИН (по К. Джини) Рис. 6.1. Классификация средних величин
Вариационный ряд — это статистический ряд распределения значений изучаемого количественного признака. Вариационные ряды бывают следующих видов:
Вариационный ряд состоит из вариант (v — vario) и соответствующих им частот (р — pars или иногда f — frequency). Вариантой (v) называют каждое числовое значение изучаемого признака. Частота (р) — абсолютная численность отдельных вариант в совокупности, указывающая, сколько раз встречается данная варианта в вариационном ряду. Общее число случаев наблюдений, из которых состоит вариационный ряд, обозначают буквой п (numerus). Если исследователь имеет не более 30 наблюдений, то достаточно все значения признака расположить в нарастающем или в убывающем порядке (от максимальной варианты до минимальной или наоборот) и указать частоту каждой варианты. При большом числе наблюдений (более 30) вариационный ряд рекомендуется сгруппировать. Простой вариационный ряд представляет собой ряд, в котором каждая варианта представлена единым наблюдением, т. е. ее частота равна единице. Во взвешенном вариационном ряду каждому значению варианты соответствует разное число частот. Сгруппированный (интервальный) ряд имеет варианты, соединенные в группы, объединяющие их по величине в пределах определенного интервала. В несгруппированном ряду каждой отдельной варианте соответствует определенная частота. В прерывном (дискретном) ряду варианты выражены в виде целых (дискретных) чисел, а в непрерывном ряду варианты могут быть выражены дробным и сколь угодно малым числом.
Четный вариационный ряд содержит четное число наблюдений (п), нечетный ряд — нечетное число п. В симметричном вариационном ряду все виды средних величин совпадают либо практически очень близки. Мультимодальный ряд характеризуется неоднородностью. Существуют различные способы определения средних величин в вариационных рядах. Под средней арифметической величиной (М) в статистике понимают обобщенную величину, которая характеризует типичный размер или средний уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени. Средняя арифметическая величина имеет следующие свойства:
Средняя арифметическая величина рассчитывается несколькими способами:
где А — условная средняя (любая варианта вариационного ряда, чаще всего в качестве условной средней берется мода — Мо);; — интервал (число вариант, входящих в каждую группу); а = М — А — условное отклонение каждой варианты от условной средней (условное отклонение).
Средняя арифметическая одним числом характеризует совокупность, обобщая то, что свойственно всем ее вариантам, поэтому она имеет ту же размерность, что и каждая из вариант.
Сразу отметим, что реальность выдвижения этой величины в качестве нормативной обусловлена тем, что это не максимальный, труднодостижимый результат, а обобщенный опыт многих передовых образцов. Средняя прогрессивная — это средняя той части совокупности, варианты которой превышают среднюю всей совокупности. Применение средней прогрессивной в медицинской практике требует известной осторожности, так как своеобразие медицинской деятельности заключается в ее качественной стороне. Увеличение нагрузки врача или занятости койки возможно лишь в узких пределах и может сказаться на качестве лечения. Можно пользоваться средней прогрессивной при изучении деятельности лечебно-вспомогательных (например, физиотерапевтических) отделений, при изучении показателей в поликлинической практике и практике семейного врача, при учете результатов физических тренировок и достижений спортсменов. Таким образом, различия применяемых средних величин могут быть отражены в следующих определениях: средняя арифметическая (М) является результативной суммой всех влияний, в ее формировании принимают участие все варианты без исключения, в том числе и крайние варианты, имеющие подчас эксквизитный характер. Медиана и мода, в отличие от средней арифметической, не зависят от величины всех индивидуальных значений, т. е. всех членов вариационного ряда, а обусловливаются относительным расположением или распределением вариант. Поэтому медиану и моду даже называют описательными или позиционными средними, так как они характеризуют главнейшие свойства данного распределения. Средняя арифметическая характеризует всю массу наблюдений без исключения; медиана и мода — основную массу, без учета воздействия крайних вариант, зависящих иногда от случайных причин. Существует несколько вопросов, которые необходимо учитывать при анализе средних величин.
Первый вопрос может и должен быть решен в свете качественного анализа, определяющего сущность изучаемых явлений. Например, нельзя изучать физическое развитие вообще, без учета пола и возраста. Или вычислять средние сроки лечения больных в терапевтическом отделении без распределения их по отдельным нозологическим формам. Необходимое число наблюдений определяется конкретно для каждого исследования при помощи средних ошибок. Следует избегать формального, шаблонного подхода: «не менее 100 наблюдений в каждой группе», т. к. этого может быть и много, и мало. В связи с этим всегда следует помнить об опасности усреднённых данных. Необходимо применять только групповые средние, приводя наряду с ними показатели максимума и минимума колебаний. Средняя величина представляет собой средство обобщения на базе группировок: можно вычислять, наряду с групповыми или частными, и общую среднюю для всей совокупности. Но совокупность обязательно должна быть качественно однородной, т. к. в разнотипной, разносоставной совокупности средняя теряет свой смысл и не отражает подлинной действительности. Из таблицы 6.1. видно, что в ряду, где частоты не равны единице и не равны между собой, нельзя складывать значение вариант и, следовательно, простая средняя здесь неприменима. В этом случае надо вычислить среднюю арифметическую взвешенную, которая получается как сумма произведений вариант на соответствующие частоты, деленная на общее число наблюдений. При этом каждая варианта умножается на свою частоту. Она как бы «взвешивается», и при этом частоты служат «весами». Таблица 6.1 Распределение больных по срокам лечения
Если варианты обозначить буквой V, частоты — буквой р, общее число наблюдений буквой N (Numerus), арифметическую сумму — буквой S, то формула средней арифметической выразится следующим образом:
Нетрудно заметить, что эта формула средней арифметической взвешенной является пригодной и для средней арифметической простой. Т. к. в последнем случае частоты равны единице, то умножение излишне, и мы ограничиваемся простым сложением. Средняя арифметическая простая — это частный случай средней арифметической взвешенной. Иногда на практике средние величины получают и без наличия вариационного ряда. Например, путем деления общего числа поликлинических посещений на число жителей обслуживаемого района или путем деления общей суммы койко-дней, проведенных больными в больнице, на число лечившихся больных. Наряду со средней арифметической, в санитарной статистике применяются, хотя и реже, такие виды средних, как медиана и мода.
Как видно из рисунка 6.2, при нормальном распределении все три средние величины (М, Мо, Ме) совпадают. Средняя арифметическая соответствует середине ряда, т. к. в симметричном ряду отклонения в сторону увеличения и в сторону уменьшения вариант соответственно уравновешиваются. Медиана, как центральная величина, также соответствует середине ряда. Мода, как наиболее насыщенная величина, приходится на наивысшую точку ряда, также находящуюся в его центре. Многие распределения, с которыми встречается врач на практике, являются симметричными, близкими к нормальным. В частности, это относится к показателям физического развития. Параметры такого ряда имеют большое практическое значение для легкой промышленности, для изготовления так называемых «ходовых», наиболее часто встречающихся размеров одежды и обуви.
Рис. 6.2. Распределение вариант в нормальной кривой
Поэтому для большинства вариационных рядов нет необходимости вычислять другие средние величины, кроме средней арифметической. В этом кроется объяснение упомянутого выше обстоятельства, что средняя арифметическая всегда является наиболее употребительной и чаще всего применяемой в санитарной статистике величиной. Прибегать к медиане и моде приходится при наличии асимметричных рядов. Наглядное представление об этом мы получаем при рассмотрении рисунка 6.3., на котором изображена резко асимметричная кривая распределения умерших от рака прямой кишки по срокам длительности болезни. У подавляющего большинства летальные исходы наступили в ранние сроки, но в отдельных случаях продолжительность болезни составила 96, 104 и более месяцев. Эти нетипичные, эксквизитные случаи «отягощают» среднюю арифметическую, которая равняется 25,6 месяца, в то время как мода, высчитанная по соответствующей формуле, составила 10,38 месяца, а медиана — 20,7 месяца. Очевидно, что наиболее типичной и характерной для данного явления средней величиной служит мода. Таким образом, различия в применяемых средних могут быть отражены в следующих определениях. Средняя арифметическая (М) является результативной суммой всех влияний. В ее формировании принимают участие все без исключения варианты, в том числе и крайние варианты, имеющие подчас эксквизитный характер. Медиана и мода, в отличие от средней арифметической, не зависят от величины всех индивидуальных значений, т. е. всех членов вариационного ряда, а обусловливаются относительным расположением или распределением вариант. Поэтому медиану и моду также называют описательными или позиционными средними, т. к. они характеризуют главнейшие свойства данного распределения. Особенно это касается медианы, являющейся в известном смысле, непараметрической величиной. М характеризует всю массу наблюдений, а Ме и Мо — основную массу, без учета воздействия крайних вариант, т. е. исключая крайние значения, зависящие иногда от случайных причин.
Бредфорд Хилл говорил о моде, что она отражает не столько среднюю, сколько обычную длительность течения. Если задача заключается в нахождении величины, отражающей всю сумму индивидуальных значений вариант, то применяют М, если же надо определить величину, соответствующую главнейшим значениям вариант, применяют Мо. В примере, приведенном на рис. 4, нас интересует не столько средний срок длительности течения болезни, сколько тот срок, до которого практически остается в живых наибольшее число больных, т. е. модальный срок. Незначительная частота моды ее обесценивает. В тех случаях, когда в асимметричных рядах мода по частоте своей не намного отличается от соседних вариант, предпочтительнее пользоваться медианой. Бимодальный (или мультимодальный) ряд распределения всегда внушает подозрение своей неоднородностью, когда две вершины ряда получены в результате смешения качественно различных совокупностей. Так, например, при изучении физического развития школьников без учета их пола получаются две моды (одна из них характеризует мальчиков, другая — девочек). Подобное явление может наблюдаться в исследовании физического развития призывников при игнорировании национально-этнических групп. Если же вскрыть и устранить причину бимодального ряда не удается, то лучше пользоваться медианой. Следующим видом средних величин, подлежащих нашему рассмотрению, является средняя прогрессивная. Средняя прогрессивная (табл. 6.2.) имеет огромное значение в экономической статистике и значительно меньшее в санитарной статистике. Дело в том, что при вычислении обычной средней арифметической в нее входят все предприятия по уровню производительности труда, все колхозы по уровню урожайности и этим самым в подсчет входят и отстающие предприятия, с низким показателем. Таблица 6.2 Средняя прогрессивная и методика ее вычисления
Средняя арифметическая: Средняя прогрессивная: Таким образом, средняя арифметическая не может быть принята в качестве правильно построенного планового норматива. Методика получения средней прогрессивной заключается в том, что её вычисляют не для всего круга предприятий или учреждений, а только для передовых, показывающих лучшие образцы работы. Границей, разделяющей их совокупность, служит средняя арифметическая, т. е. средний уровень. По той части предприятий, которая находится выше этого среднего уровня, вычисляется новая, вторая средняя величина. Это и будет средняя прогрессивная. Сразу отметим, что реальность выдвижения этой величины в качестве нормативной обусловлена тем, что это не максимальный, трудно достижимый результат, а обобщенный опыт многих передовых образцов. Средняя прогрессивная — это средняя той части совокупности, варианты которой превышают среднюю всей совокупности. Применение средней прогрессивной в санитарно-статистической практике требует известной осторожности, т. к. своеобразие медицинской деятельности заключается в ее качественной стороне. Увеличение нагрузки врача или занятости койки возможно лишь в узких пределах и может сказаться на качестве лечения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.071 с.) |
 Для характеристики физического развития, основных антропометрических признаков (морфологических и функциональных: рост, масса тела, окружность груди, спирометрия, динамометрия, становая сила и др.) и их динамики (средние величины прироста или убыли признака). Разработка этих показателей и их сочетаний в виде региональных стандартов имеет большое практическое значение для анализа здоровья населения, в особенности его детских групп, а также спортсменов, военнослужащих и лиц, находящихся на диспансерном учете.
Для характеристики физического развития, основных антропометрических признаков (морфологических и функциональных: рост, масса тела, окружность груди, спирометрия, динамометрия, становая сила и др.) и их динамики (средние величины прироста или убыли признака). Разработка этих показателей и их сочетаний в виде региональных стандартов имеет большое практическое значение для анализа здоровья населения, в особенности его детских групп, а также спортсменов, военнослужащих и лиц, находящихся на диспансерном учете.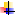 простые и взвешенные;
простые и взвешенные; в строго симметричном ряду средняя занимает срединное положение; М = Мо = Ме, т. е. средняя арифметическая, мода и медиана совпадают или близко прилежат друг к другу;
в строго симметричном ряду средняя занимает срединное положение; М = Мо = Ме, т. е. средняя арифметическая, мода и медиана совпадают или близко прилежат друг к другу; простая средняя арифметическая вычисляется на простых несгруппированных рядах, когда варианты встречаются с частотой, равной единице:
простая средняя арифметическая вычисляется на простых несгруппированных рядах, когда варианты встречаются с частотой, равной единице: дня.
дня. .
. Медиана (обозначаемая буквами Ме) — это серединная, центральная варианта, делящая вариационный ряд пополам, на две равные части.Таким образом, медиана находится на центральном месте, от которого отстоит одинаковое число и больших, и меньших вариант (и в сторону минуса, и в сторону плюса). Приближенное нахождение медианы в простом, несгруппированном ряду производится очень легко, особенно если число наблюдений нечетное. Так, например, в табл. 6, где число наблюдений составляет 33, медианой будет 17-я по счету, т. к. в обе стороны от нее отстоит по 16 наблюдений. Путем простого подсчета убеждаемся, что значение 17-й величины составляет 22. Следовательно, медиана равна 22 дням. В ряду с четным числом наблюдений в центре находятся две величины. Иногда они одинаковы по своему значению, и тогда не возникает затруднений в приближенном определении медианы.
Медиана (обозначаемая буквами Ме) — это серединная, центральная варианта, делящая вариационный ряд пополам, на две равные части.Таким образом, медиана находится на центральном месте, от которого отстоит одинаковое число и больших, и меньших вариант (и в сторону минуса, и в сторону плюса). Приближенное нахождение медианы в простом, несгруппированном ряду производится очень легко, особенно если число наблюдений нечетное. Так, например, в табл. 6, где число наблюдений составляет 33, медианой будет 17-я по счету, т. к. в обе стороны от нее отстоит по 16 наблюдений. Путем простого подсчета убеждаемся, что значение 17-й величины составляет 22. Следовательно, медиана равна 22 дням. В ряду с четным числом наблюдений в центре находятся две величины. Иногда они одинаковы по своему значению, и тогда не возникает затруднений в приближенном определении медианы.

 дня.
дня. дня.
дня.


