Как и для параболического сплайна, сначала находим номер  отрезка, содержащего точку
отрезка, содержащего точку  , по формуле
, по формуле  . Зная все коэффициенты
. Зная все коэффициенты  ,
,  ,
,  ,
,  и номер отрезка
и номер отрезка  , находим значение естественного интерполяционного кубического сплайна в точке
, находим значение естественного интерполяционного кубического сплайна в точке  , принадлежащей отрезку
, принадлежащей отрезку  ,
,
 .
.
Для вычисления значений сплайна и его производных в точке  , введем дополнительные коэффициенты:
, введем дополнительные коэффициенты:  ,
,  ,
,  . Ранее уже был определен коэффициент
. Ранее уже был определен коэффициент  .
.
Значения первой и второй производных естественного интерполяционного кубического сплайна вычисляются по формулам
 ,
,  .
.
Сложность вычислительного алгоритма построения интерполяционного кубического сплайна та же, что и у параболического и линейного сплайнов. Число арифметических действий, необходимых для построения интерполяционного кубического сплайна, пропорционально числу отрезков ( ), объем памяти также пропорционален числу отрезков (
), объем памяти также пропорционален числу отрезков ( ).
).
Так как интерполяционный кубический сплайн хорошо приближает гладкие функции (теорема о сходимости, оценка погрешности) и имеет минимальную сложность, то на практике для гладких функций при решении задач интерполяции и численного дифференцирования используется именно интерполяционный кубический сплайн.
2.4. B-сплайны
B-сплайны (базовые, фундаментальные, базисные сплайны) – это функции, определенные на отрезке  и образующие некоторый базис, который позволяет представить любой сплайн в виде линейной комбинации соответствующих B-сплайнов. Так же, как произвольный вектор
и образующие некоторый базис, который позволяет представить любой сплайн в виде линейной комбинации соответствующих B-сплайнов. Так же, как произвольный вектор  , принадлежащий плоскости
, принадлежащий плоскости  , можно единственным образом представить в виде линейной комбинации базисных векторов
, можно единственным образом представить в виде линейной комбинации базисных векторов  и
и  , а именно
, а именно  , так и произвольный сплайн можно единственным образом представить в виде линейной комбинации соответствующих базисных сплайнов.
, так и произвольный сплайн можно единственным образом представить в виде линейной комбинации соответствующих базисных сплайнов.
B-сплайном нулевой степени, построенным на отрезке  по сетке
по сетке  , называется функция вида:
, называется функция вида:

 B-сплайн
B-сплайн  степени
степени  может быть отличен от нуля только на
может быть отличен от нуля только на 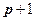 отрезках
отрезках  , примыкающих друг к другу. Например, кубический B-сплайн
, примыкающих друг к другу. Например, кубический B-сплайн  отличен от нуля на отрезке
отличен от нуля на отрезке  , а линейный B – сплайн отличен от нуля на отрезке
, а линейный B – сплайн отличен от нуля на отрезке  (рис. 2.2).
(рис. 2.2).
Любой линейный сплайн на отрезке  можно представить в виде линейной комбинации B-сплайнов первой степени:
можно представить в виде линейной комбинации B-сплайнов первой степени:
 .
.
Любой кубический сплайн на отрезке  также может быть единственным образом представлен в виде линейной комбинации кубических B-сплайнов. Такой подход позволяет уменьшить объем памяти, необходимый для построения сплайна.
также может быть единственным образом представлен в виде линейной комбинации кубических B-сплайнов. Такой подход позволяет уменьшить объем памяти, необходимый для построения сплайна.
2.5. Построение интерполяционных сплайновых кривых
при помощи сплайн - функций
 Ранее мы всегда оговаривали, что в интерполяционной таблице все узлы сетки
Ранее мы всегда оговаривали, что в интерполяционной таблице все узлы сетки 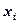 различны и упорядочены по возрастанию
различны и упорядочены по возрастанию  . Как строить интерполяционные сплайны, если узлы сетки совпадают между собой или не упорядочены по возрастанию? В таких случаях решением задачи интерполяции являются кривые, заданные параметрически
. Как строить интерполяционные сплайны, если узлы сетки совпадают между собой или не упорядочены по возрастанию? В таких случаях решением задачи интерполяции являются кривые, заданные параметрически  Приведем алгоритм для описания параметрических уравнений кривой, описанный в книге /9/.
Приведем алгоритм для описания параметрических уравнений кривой, описанный в книге /9/.
Пусть задана интерполяционная таблица  ,
,  , причем узлы сетки
, причем узлы сетки 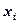 не упорядочены и могут совпадать между собой. Требуется построить кривую, последовательно проходящую через все точки интерполяционной таблицы.
не упорядочены и могут совпадать между собой. Требуется построить кривую, последовательно проходящую через все точки интерполяционной таблицы.
1. На произвольном отрезке  изменения параметра
изменения параметра  вводится вспомогательная сетка, узлы которой упорядочены и различны:
вводится вспомогательная сетка, узлы которой упорядочены и различны:  . Число узлов сетки совпадает с числом заданных точек
. Число узлов сетки совпадает с числом заданных точек  . В качестве отрезка
. В качестве отрезка  можно выбрать отрезок [0,1], а шаг
можно выбрать отрезок [0,1], а шаг 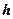 по переменной
по переменной 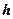 выбрать равномерный, т.е.
выбрать равномерный, т.е.  .
.
2. По известной интерполяционной таблице  ,
,  и вспомогательной сетке строятся две вспомогательные интерполяционные таблицы:
и вспомогательной сетке строятся две вспомогательные интерполяционные таблицы:
 ,
,  ,
,  .
.
Отметим, что в построенных вспомогательных интерполяционных таблицах узлы сетки упорядочены и различны, и по этим таблицам единственным образом могут быть построены интерполяционные сплайны  и
и  .
.
3. По каждой из вспомогательных интерполяционных таблиц строятся соответствующие интерполяционные сплайн – функции  и
и  .
.
Таким образом, получается кривая, последовательно проходящая через все точки заданной интерполяционной таблицы (рис. 2.3).
2.6. Примеры решения задач
Задача 1. По данной интерполяционной таблице построить интерполяционный линейный сплайн.
Решение. Пусть задана интерполяционная таблица:
Таким образом, задано  ,
,  ,
, 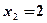 и
и  ,
, 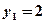 ,
,  ,
,  .
.
Линейный сплайн в данном случае ( ) определяется формулой
) определяется формулой

Для нахождения коэффициентов  и
и  воспользуемся формулами
воспользуемся формулами  и
и  ,
,  . Получаем
. Получаем  ,
,  ,
,  ,
,  . Запишем
. Запишем

Проверим, что  - интерполяционный сплайн, для этого вычислим значения
- интерполяционный сплайн, для этого вычислим значения  при
при  Получаем
Получаем 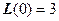 ,
,  ,
,  , следовательно,
, следовательно,  - интерполяционный сплайн.
- интерполяционный сплайн.
Ответ: 
Задача 2. Построить систему линейных уравнений для нахождения коэффициентов интерполяционного параболического сплайна по заданной интерполяционной таблице и краевому условию.
Решение. Пусть задана интерполяционная таблица
и краевое условие: 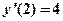 , т.е.
, т.е.  ,
,  ,
, 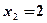 ;
;  ,
, 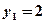 ,
,  ,
,  .
.
Решение задачи заключается в построении системы линейных уравнений относительно коэффициентов параболического сплайна  . Так как
. Так как  , то параболический сплайн записывается следующим образом:
, то параболический сплайн записывается следующим образом:

Неизвестных коэффициентов  ,
,  и
и  шесть, требуется записать шесть линейных уравнений. Первые три уравнения вытекают из условий:
шесть, требуется записать шесть линейных уравнений. Первые три уравнения вытекают из условий:  ,
,  . Получаем:
. Получаем:  ,
,  ,
, 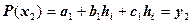 , где
, где  ,
, 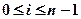 . В нашем случае равномерный шаг
. В нашем случае равномерный шаг 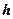 равен 1. Получаем три уравнения:
равен 1. Получаем три уравнения:  ,
,  ,
,  .
.
Одно уравнение вытекает из краевого условия 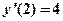 . Запишем формулу для производной сплайна:
. Запишем формулу для производной сплайна:

Из краевого условия получаем уравнение  или
или  . Еще два уравнения получаем из условия, что параболический сплайн является непрерывно дифференцируемой функцией во всех внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел
. Еще два уравнения получаем из условия, что параболический сплайн является непрерывно дифференцируемой функцией во всех внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел 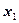 . Запишем формулу сплайна в виде:
. Запишем формулу сплайна в виде:
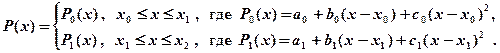
Из непрерывности сплайна вытекает уравнение  или
или  , а из непрерывности производной сплайна вытекает, что
, а из непрерывности производной сплайна вытекает, что 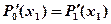 или
или  .
.
Ответ: Запишем систему линейных уравнений:
 Отметим, что мы рассмотрели случай правого краевого условия (
Отметим, что мы рассмотрели случай правого краевого условия ( ). Случай левого краевого условия рассматривается аналогично. Например, если вместо условия
). Случай левого краевого условия рассматривается аналогично. Например, если вместо условия  задано условие
задано условие  , то в системе линейных уравнений четвертое уравнение нужно заменить на следующее:
, то в системе линейных уравнений четвертое уравнение нужно заменить на следующее: 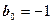 .
.
Задача 3. Построить систему линейных уравнений для нахождения коэффициентов интерполяционного кубического сплайна по заданным краевым условиям и интерполяционной таблице.
Решение. Пусть задана интерполяционная таблица
и краевые условия: 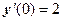 и
и 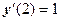 , т.е.
, т.е.  ,
,  ,
,  ,
,  ,
,  ,
, 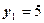 ,
,  ,
,  . Требуется построить систему линейных уравнений относительно коэффициентов кубического сплайна
. Требуется построить систему линейных уравнений относительно коэффициентов кубического сплайна  . Так как
. Так как  , то кубический сплайн записывается следующим образом:
, то кубический сплайн записывается следующим образом:

Неизвестных коэффициентов восемь, требуется записать восемь линейных уравнений. Первые три уравнения вытекают из условий 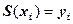 ,
,  . Получаем:
. Получаем:  ,
,  ,
,  . Запишем первые три уравнения:
. Запишем первые три уравнения:  ,
,  ,
,  . Два уравнения вытекают из краевых условий. Запишем формулу для производной сплайна:
. Два уравнения вытекают из краевых условий. Запишем формулу для производной сплайна:
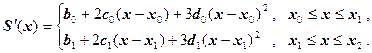
Из левого краевого условия  вытекает уравнение
вытекает уравнение  . Из правого условия
. Из правого условия  вытекает уравнение
вытекает уравнение  . Еще три уравнения получаем из условия, что кубический сплайн является дважды непрерывно дифференцируемой функцией во всех точках отрезка
. Еще три уравнения получаем из условия, что кубический сплайн является дважды непрерывно дифференцируемой функцией во всех точках отрезка  , в том числе и во внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел
, в том числе и во внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел 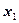 . Запишем формулу сплайна в виде:
. Запишем формулу сплайна в виде:

Из непрерывности сплайна вытекает уравнение  . А из непрерывности первой и второй производной сплайна следуют уравнения
. А из непрерывности первой и второй производной сплайна следуют уравнения  и
и  . Получаем:
. Получаем:
 ,
,  ,
,  .
.
Ответ: Запишем систему линейных уравнений:

Задача 4. Определить, является ли функция  линейным сплайном, где
линейным сплайном, где
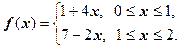
Решение. Запишем функцию  в виде:
в виде:

 . Для того чтобы функция
. Для того чтобы функция  являлась линейным сплайном, одновременно должны выполняться два условия:
являлась линейным сплайном, одновременно должны выполняться два условия:
1) функции  и
и  - полиномы первой степени;
- полиномы первой степени;
2) функция  - непрерывная функция на отрезке
- непрерывная функция на отрезке  .
.
Если хотя бы одно из этих условий не выполнено, то функция  не является линейным сплайном, если же они выполняются одновременно, то
не является линейным сплайном, если же они выполняются одновременно, то  является линейным сплайном. Проверим эти условия. Первое условие выполнено, так как функции
является линейным сплайном. Проверим эти условия. Первое условие выполнено, так как функции  и
и  являются полиномами первой степени. Второе условие, при выполнении первого условия, достаточно проверить во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел
являются полиномами первой степени. Второе условие, при выполнении первого условия, достаточно проверить во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел 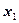 . Поэтому второе условие при выполнении первого условия достаточно проверить только в точке
. Поэтому второе условие при выполнении первого условия достаточно проверить только в точке 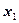 , т.е. нужно проверить выполнение равенства
, т.е. нужно проверить выполнение равенства  . Вычислим
. Вычислим  и
и  . Так как
. Так как  , то
, то  - непрерывная функция на отрезке
- непрерывная функция на отрезке  . Оба условия выполнены, следовательно, функция
. Оба условия выполнены, следовательно, функция  является линейным сплайном.
является линейным сплайном.
Ответ: функция  является линейным сплайном.
является линейным сплайном.
Задача 5. Определить, является ли функция  параболическим сплайном, удовлетворяющим краевому условию
параболическим сплайном, удовлетворяющим краевому условию  , где
, где  ,
,

Решение. Запишем функцию  в виде:
в виде:

 ,
,  ,
,  . Для того чтобы функция
. Для того чтобы функция  являлась параболическим сплайном, удовлетворяющим краевому условию
являлась параболическим сплайном, удовлетворяющим краевому условию  , одновременно должны выполняться три условия:
, одновременно должны выполняться три условия:
1. функции  и
и  - полиномы второй степени;
- полиномы второй степени;
2. функция  - непрерывно дифференцируемая функция на отрезке
- непрерывно дифференцируемая функция на отрезке  ;
;
3. функция  удовлетворяет краевому условию
удовлетворяет краевому условию  .
.
Если хотя бы одно из этих условий не выполнено, то функция  не является параболическим сплайном, удовлетворяющим заданному краевому условию. Проверим эти условия. Первое условие выполнено, так как функции
не является параболическим сплайном, удовлетворяющим заданному краевому условию. Проверим эти условия. Первое условие выполнено, так как функции  и
и  являются полиномами второй степени. Второе условие, при выполнении первого условия, достаточно проверить только во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел
являются полиномами второй степени. Второе условие, при выполнении первого условия, достаточно проверить только во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел 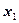 . Поэтому второе условие, при выполнении первого условия, достаточно проверить только в точке
. Поэтому второе условие, при выполнении первого условия, достаточно проверить только в точке 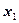 , т.е. нужно проверить выполнение равенств
, т.е. нужно проверить выполнение равенств  и
и  . Вычислим
. Вычислим  ,
,  ;
; 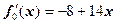 ,
,  ,
,  ,
,  . Так как
. Так как  , то
, то  - непрерывно дифференцируемая функция на отрезке
- непрерывно дифференцируемая функция на отрезке  . Для проверки третьего условия вычислим значение производной функции
. Для проверки третьего условия вычислим значение производной функции  в точке
в точке  :
:  . Так как
. Так как  , то третье условие выполнено.
, то третье условие выполнено.
Три условия выполняются одновременно, следовательно, функция  является параболическим сплайном, удовлетворяющим краевому условию
является параболическим сплайном, удовлетворяющим краевому условию  .
.
Ответ: функция  является параболическим сплайном, удовлетворяющим краевому условию
является параболическим сплайном, удовлетворяющим краевому условию  .
.
Задача 6. Определить является ли функция  естественным кубическим сплайном, где:
естественным кубическим сплайном, где:

Решение. Запишем функцию  в виде:
в виде:

 ,
,  ,
,  . Для того чтобы функция
. Для того чтобы функция  являлась естественным кубическим сплайном, одновременно должны выполняться три условия:
являлась естественным кубическим сплайном, одновременно должны выполняться три условия:
1. функции  и
и  - полиномы третьей степени;
- полиномы третьей степени;
2. функция  - дважды непрерывно дифференцируемая функция на отрезке
- дважды непрерывно дифференцируемая функция на отрезке  ;
;
3. функция  удовлетворяет двум краевым условиям:
удовлетворяет двум краевым условиям:  ,
,  .
.
Если хотя бы одно из этих условий не выполнено, то функция  не является естественным кубическим сплайном. Проверим эти условия. Первое условие выполнено, так как функции
не является естественным кубическим сплайном. Проверим эти условия. Первое условие выполнено, так как функции  и
и  являются полиномами третьей степени. Второе условие, при выполнении первого условия, достаточно проверить только во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел
являются полиномами третьей степени. Второе условие, при выполнении первого условия, достаточно проверить только во внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел 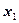 . Поэтому второе условие, при выполнении первого условия, достаточно проверить только в точке
. Поэтому второе условие, при выполнении первого условия, достаточно проверить только в точке 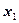 , т.е. нужно проверить выполнение равенств:
, т.е. нужно проверить выполнение равенств:  ,
,  и
и  . Вычислим
. Вычислим  ,
,  ;
;  ,
,  ,
,  ,
,  ;
;  ,
,  ,
,  ,
,  . Так как
. Так как 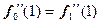 , то
, то  - дважды непрерывно дифференцируемая функция на отрезке
- дважды непрерывно дифференцируемая функция на отрезке  . Для проверки третьего условия вычислим значения второй производной функции
. Для проверки третьего условия вычислим значения второй производной функции  в краевых точках:
в краевых точках:  и
и  . Третье условие выполнено.
. Третье условие выполнено.
Три условия выполняются одновременно, следовательно, функция  является естественным кубическим сплайном.
является естественным кубическим сплайном.
Ответ: функция  является естественным кубическим сплайном.
является естественным кубическим сплайном.
3. Сглаживание кубическими сплайнами
На практике часто вместо интерполяционной таблицы  известна таблица экспериментальных данных
известна таблица экспериментальных данных  где
где  ,
,  - погрешность, таким образом, вместо значений функции
- погрешность, таким образом, вместо значений функции  нам известны результаты измерений, содержащие погрешность. Возникают задачи восстановления функции
нам известны результаты измерений, содержащие погрешность. Возникают задачи восстановления функции  и вычисления производной функции по зашумленным данным. Использование интерполяции в такой ситуации нецелесообразно, т.к. интерполирующая кривая будет существенно зависеть от погрешности (рис. 3.1), а ее производная будет сильно отличаться от
и вычисления производной функции по зашумленным данным. Использование интерполяции в такой ситуации нецелесообразно, т.к. интерполирующая кривая будет существенно зависеть от погрешности (рис. 3.1), а ее производная будет сильно отличаться от  (рис. 3.2) /9/.
(рис. 3.2) /9/.
Если заранее известно, что результаты измерений  содержат погрешности
содержат погрешности  , то естественно рассматривать не задачу интерполяции, а задачу сглаживания, т.е. задачу построения гладкой (непрерывно дифференцируемой, дважды непрерывно дифференцируемой) функции, которая проходила бы не через заданные точки
, то естественно рассматривать не задачу интерполяции, а задачу сглаживания, т.е. задачу построения гладкой (непрерывно дифференцируемой, дважды непрерывно дифференцируемой) функции, которая проходила бы не через заданные точки  а вблизи них. На рис. 3.1 /9/ приведен график функции
а вблизи них. На рис. 3.1 /9/ приведен график функции 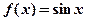 на отрезке
на отрезке  точками отмечены результаты измерений
точками отмечены результаты измерений  выведена интерполяционная кривая
выведена интерполяционная кривая  и сглаживающая кривая
и сглаживающая кривая  (пунктиром). На рис. 3.2 /9/ приведены графики производной
(пунктиром). На рис. 3.2 /9/ приведены графики производной  на отрезке
на отрезке  производной интерполяционной кривой
производной интерполяционной кривой  и производной сглаживающей кривой
и производной сглаживающей кривой  (пунктиром).
(пунктиром).
Рекомендуемая литература: /1, 4, 9/.
3.1. Постановка задачи сглаживания
В литературе приводятся различные формулировки постановки задачи сглаживания. Приведем две из них.
1. Пусть на отрезке  задана таблица
задана таблица  , где
, где  погрешность.
погрешность.
Требуется построить гладкую функцию  , которая достаточно близка к функции
, которая достаточно близка к функции  на отрезке
на отрезке  .
.
2. Пусть на отрезке  задана таблица
задана таблица  , где
, где 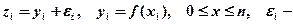 погрешность, и положительные числа
погрешность, и положительные числа  Требуется построить гладкую функцию
Требуется построить гладкую функцию  , такую что
, такую что 
Задача сглаживания заключается в восстановлении гладкой функции по зашумленным табличным данным. Понятно, что эта задача, как и задача интерполяции, имеет множество решений. Накладывая определенные ограничения на функцию  , получаем задачу, имеющую единственное решение. На практике для решения задачи сглаживания чаще всего используются сглаживающие кубические сплайны. Мы рассмотрим естественный сглаживающий кубический сплайн (остальные сглаживающие кубические сплайны отличаются от него краевыми условиями).
, получаем задачу, имеющую единственное решение. На практике для решения задачи сглаживания чаще всего используются сглаживающие кубические сплайны. Мы рассмотрим естественный сглаживающий кубический сплайн (остальные сглаживающие кубические сплайны отличаются от него краевыми условиями).
Определение естественного сглаживающего кубического сплайна
Пусть на отрезке  задана сетка
задана сетка  в узлах которой заданы значения
в узлах которой заданы значения  Естественным сглаживающим кубическим сплайном называется функция
Естественным сглаживающим кубическим сплайном называется функция  , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) функция  - дважды непрерывно дифференцируемая функция на
- дважды непрерывно дифференцируемая функция на 
2) на каждом из отрезков  функция
функция  является полиномом третьей степени вида
является полиномом третьей степени вида 
3) функция  доставляет минимум функционалу
доставляет минимум функционалу  где
где  - заданные положительные числа, называемые весовыми коэффициентами;
- заданные положительные числа, называемые весовыми коэффициентами;
4) краевым условием 
Пример. Функция

является естественным сглаживающим кубическим сплайном, определенным на отрезке  и построенным по следующей таблице:
и построенным по следующей таблице:
при 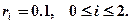
Теорема существования и единственности. Пусть заданы положительные числа 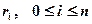 и таблица
и таблица  причем все узлы сетки различны
причем все узлы сетки различны  при
при  . Тогда существует единственный естественный сглаживающий кубический сплайн на отрезке
. Тогда существует единственный естественный сглаживающий кубический сплайн на отрезке 
Другими словами если заданы весовые коэффициенты  и таблица экспериментальных данных
и таблица экспериментальных данных  в которой все узлы сетки различны, то существует единственный естественный сглаживающий кубический сплайн, соответствующий этой таблице и весовым коэффициентам.
в которой все узлы сетки различны, то существует единственный естественный сглаживающий кубический сплайн, соответствующий этой таблице и весовым коэффициентам.
Производная сглаживающего кубического сплайна – это непрерывно дифференцируемая, кусочно–параболическая функция, то есть параболический сплайн: 
Замечание. Весовые коэффициенты  задаваемые пользователем, позволяют в известной степени управлять свойствами сглаживающих сплайнов. Если все
задаваемые пользователем, позволяют в известной степени управлять свойствами сглаживающих сплайнов. Если все  то
то  и сглаживающий сплайн становится интерполяционным. Таким образом, интерполяционный кубический сплайн можно рассматривать как частный случай сглаживающего кубического сплайна (при
и сглаживающий сплайн становится интерполяционным. Таким образом, интерполяционный кубический сплайн можно рассматривать как частный случай сглаживающего кубического сплайна (при 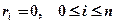 ). Отметим, что чем меньше погрешность
). Отметим, что чем меньше погрешность  , тем меньше должны быть весовые коэффициенты
, тем меньше должны быть весовые коэффициенты  Если же необходимо, чтобы сглаживающий кубический сплайн прошел через точку
Если же необходимо, чтобы сглаживающий кубический сплайн прошел через точку  то соответствующий весовой множитель
то соответствующий весовой множитель  следует положить равным нулю. В практических вычислениях выбор величин
следует положить равным нулю. В практических вычислениях выбор величин  является важным вопросом, для решения которого используются различные подходы /9/.
является важным вопросом, для решения которого используются различные подходы /9/.
3.2. Построение естественного сглаживающего
кубического сплайна
Для построения естественного сглаживающего кубического сплайна

необходимо уметь вычислять коэффициенты сплайна  и
и  Опишем алгоритм нахождения коэффициентов сплайна, для реализации которого требуется
Опишем алгоритм нахождения коэффициентов сплайна, для реализации которого требуется  арифметических действий и
арифметических действий и  памяти.
памяти.
1. Коэффициенты  находятся из решения системы линейных уравнений размерности
находятся из решения системы линейных уравнений размерности  с невырожденной пятидиагональной матрицей методом прогонки (п.п.1.2). Запишем эту систему линейных уравнений для случая равномерного шага и одинаковых значений весовых коэффициентов
с невырожденной пятидиагональной матрицей методом прогонки (п.п.1.2). Запишем эту систему линейных уравнений для случая равномерного шага и одинаковых значений весовых коэффициентов 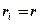

где 

Отметим, что при  мы получаем систему линейных уравнений с трехдиагональной матрицей (случай естественного интерполяционного кубического сплайна).
мы получаем систему линейных уравнений с трехдиагональной матрицей (случай естественного интерполяционного кубического сплайна).
2. После нахождения коэффициентов  находим
находим  где
где  - это значения естественного сглаживающего кубического сплайна в узлах сетки,
- это значения естественного сглаживающего кубического сплайна в узлах сетки,  Значения
Значения  находится по следующим формулам:
находится по следующим формулам:

3. Зная  и
и  , находим коэффициенты
, находим коэффициенты  ,
,  и
и  по явным формулам
по явным формулам

Отметим, что мы сразу привели формулы для дополнительных коэффициентов  и
и  , которые потребуются для вычисления значения сплайна и его производных при
, которые потребуются для вычисления значения сплайна и его производных при 


 отрезка, содержащего точку
отрезка, содержащего точку  , по формуле
, по формуле  . Зная все коэффициенты
. Зная все коэффициенты  ,
,  ,
,  ,
,  и номер отрезка
и номер отрезка  ,
, .
. , введем дополнительные коэффициенты:
, введем дополнительные коэффициенты:  ,
,  ,
,  . Ранее уже был определен коэффициент
. Ранее уже был определен коэффициент  .
. ,
,  .
. ), объем памяти также пропорционален числу отрезков (
), объем памяти также пропорционален числу отрезков ( , принадлежащий плоскости
, принадлежащий плоскости  , можно единственным образом представить в виде линейной комбинации базисных векторов
, можно единственным образом представить в виде линейной комбинации базисных векторов  и
и  , а именно
, а именно  , так и произвольный сплайн можно единственным образом представить в виде линейной комбинации соответствующих базисных сплайнов.
, так и произвольный сплайн можно единственным образом представить в виде линейной комбинации соответствующих базисных сплайнов. , называется функция вида:
, называется функция вида:
 B-сплайн
B-сплайн  степени
степени  может быть отличен от нуля только на
может быть отличен от нуля только на 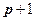 отрезках
отрезках  , примыкающих друг к другу. Например, кубический B-сплайн
, примыкающих друг к другу. Например, кубический B-сплайн  отличен от нуля на отрезке
отличен от нуля на отрезке  , а линейный B – сплайн отличен от нуля на отрезке
, а линейный B – сплайн отличен от нуля на отрезке  (рис. 2.2).
(рис. 2.2). .
. Ранее мы всегда оговаривали, что в интерполяционной таблице все узлы сетки
Ранее мы всегда оговаривали, что в интерполяционной таблице все узлы сетки 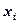 различны и упорядочены по возрастанию
различны и упорядочены по возрастанию  Приведем алгоритм для описания параметрических уравнений кривой, описанный в книге /9/.
Приведем алгоритм для описания параметрических уравнений кривой, описанный в книге /9/. ,
,  , причем узлы сетки
, причем узлы сетки  изменения параметра
изменения параметра  вводится вспомогательная сетка, узлы которой упорядочены и различны:
вводится вспомогательная сетка, узлы которой упорядочены и различны:  . Число узлов сетки совпадает с числом заданных точек
. Число узлов сетки совпадает с числом заданных точек 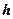 по переменной
по переменной  .
. ,
,  ,
,  и
и  .
.
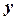
 ,
,  ,
, 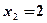 и
и  ,
, 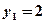 ,
,  ,
,  .
. ) определяется формулой
) определяется формулой
 и
и  ,
,  ,
,  ,
,  ,
,  . Запишем
. Запишем
 - интерполяционный сплайн, для этого вычислим значения
- интерполяционный сплайн, для этого вычислим значения  Получаем
Получаем 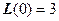 ,
,  ,
,  , следовательно,
, следовательно, 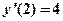 , т.е.
, т.е.  ,
,  . Так как
. Так как 
 ,
,  ,
,  ,
, 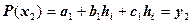 , где
, где  ,
, 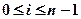 . В нашем случае равномерный шаг
. В нашем случае равномерный шаг  .
.
 или
или  . Еще два уравнения получаем из условия, что параболический сплайн является непрерывно дифференцируемой функцией во всех внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел
. Еще два уравнения получаем из условия, что параболический сплайн является непрерывно дифференцируемой функцией во всех внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел 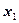 . Запишем формулу сплайна в виде:
. Запишем формулу сплайна в виде: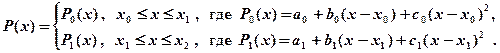
 или
или  , а из непрерывности производной сплайна вытекает, что
, а из непрерывности производной сплайна вытекает, что 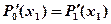 или
или  .
. Отметим, что мы рассмотрели случай правого краевого условия (
Отметим, что мы рассмотрели случай правого краевого условия ( ). Случай левого краевого условия рассматривается аналогично. Например, если вместо условия
). Случай левого краевого условия рассматривается аналогично. Например, если вместо условия  , то в системе линейных уравнений четвертое уравнение нужно заменить на следующее:
, то в системе линейных уравнений четвертое уравнение нужно заменить на следующее: 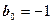 .
.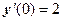 и
и 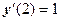 , т.е.
, т.е.  ,
,  ,
,  ,
,  ,
,  ,
, 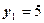 ,
,  ,
,  . Так как
. Так как 
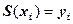 ,
,  . Получаем:
. Получаем:  . Запишем первые три уравнения:
. Запишем первые три уравнения:  ,
,  ,
,  . Два уравнения вытекают из краевых условий. Запишем формулу для производной сплайна:
. Два уравнения вытекают из краевых условий. Запишем формулу для производной сплайна: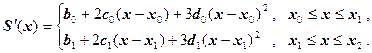
 вытекает уравнение
вытекает уравнение  . Из правого условия
. Из правого условия  вытекает уравнение
вытекает уравнение  . Еще три уравнения получаем из условия, что кубический сплайн является дважды непрерывно дифференцируемой функцией во всех точках отрезка
. Еще три уравнения получаем из условия, что кубический сплайн является дважды непрерывно дифференцируемой функцией во всех точках отрезка  , в том числе и во внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел
, в том числе и во внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел 
 . А из непрерывности первой и второй производной сплайна следуют уравнения
. А из непрерывности первой и второй производной сплайна следуют уравнения  и
и  . Получаем:
. Получаем: ,
,  ,
,  .
.
 линейным сплайном, где
линейным сплайном, где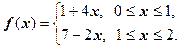

 . Для того чтобы функция
. Для того чтобы функция  и
и  - полиномы первой степени;
- полиномы первой степени; .
. . Вычислим
. Вычислим  и
и  . Так как
. Так как  , то
, то  , где
, где  ,
,

 , одновременно должны выполняться три условия:
, одновременно должны выполняться три условия: . Вычислим
. Вычислим  ,
,  ;
; 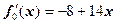 ,
,  ,
,  ,
,  . Так как
. Так как  , то
, то  в точке
в точке  :
:  . Так как
. Так как 

 ,
,  ,
,  .
. и
и  . Вычислим
. Вычислим  ,
,  ,
,  ,
,  ;
;  ,
,  ,
,  ,
,  . Так как
. Так как 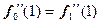 , то
, то  . Для проверки третьего условия вычислим значения второй производной функции
. Для проверки третьего условия вычислим значения второй производной функции  и
и  . Третье условие выполнено.
. Третье условие выполнено. известна таблица экспериментальных данных
известна таблица экспериментальных данных  где
где  ,
,  - погрешность, таким образом, вместо значений функции
- погрешность, таким образом, вместо значений функции  нам известны результаты измерений, содержащие погрешность. Возникают задачи восстановления функции
нам известны результаты измерений, содержащие погрешность. Возникают задачи восстановления функции  (рис. 3.2) /9/.
(рис. 3.2) /9/. содержат погрешности
содержат погрешности 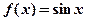 на отрезке
на отрезке  точками отмечены результаты измерений
точками отмечены результаты измерений  выведена интерполяционная кривая
выведена интерполяционная кривая  и сглаживающая кривая
и сглаживающая кривая  (пунктиром). На рис. 3.2 /9/ приведены графики производной
(пунктиром). На рис. 3.2 /9/ приведены графики производной  на отрезке
на отрезке  производной интерполяционной кривой
производной интерполяционной кривой  и производной сглаживающей кривой
и производной сглаживающей кривой  (пунктиром).
(пунктиром). задана таблица
задана таблица  , где
, где  погрешность.
погрешность. , которая достаточно близка к функции
, которая достаточно близка к функции 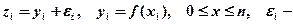 погрешность, и положительные числа
погрешность, и положительные числа  Требуется построить гладкую функцию
Требуется построить гладкую функцию 
 в узлах которой заданы значения
в узлах которой заданы значения  Естественным сглаживающим кубическим сплайном называется функция
Естественным сглаживающим кубическим сплайном называется функция 
 функция
функция 
 где
где  - заданные положительные числа, называемые весовыми коэффициентами;
- заданные положительные числа, называемые весовыми коэффициентами;

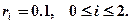
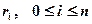 и таблица
и таблица  причем все узлы сетки различны
причем все узлы сетки различны  при
при  . Тогда существует единственный естественный сглаживающий кубический сплайн на отрезке
. Тогда существует единственный естественный сглаживающий кубический сплайн на отрезке 
 и таблица экспериментальных данных
и таблица экспериментальных данных  в которой все узлы сетки различны, то существует единственный естественный сглаживающий кубический сплайн, соответствующий этой таблице и весовым коэффициентам.
в которой все узлы сетки различны, то существует единственный естественный сглаживающий кубический сплайн, соответствующий этой таблице и весовым коэффициентам.
 задаваемые пользователем, позволяют в известной степени управлять свойствами сглаживающих сплайнов. Если все
задаваемые пользователем, позволяют в известной степени управлять свойствами сглаживающих сплайнов. Если все  то
то  и сглаживающий сплайн становится интерполяционным. Таким образом, интерполяционный кубический сплайн можно рассматривать как частный случай сглаживающего кубического сплайна (при
и сглаживающий сплайн становится интерполяционным. Таким образом, интерполяционный кубический сплайн можно рассматривать как частный случай сглаживающего кубического сплайна (при 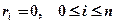 ). Отметим, что чем меньше погрешность
). Отметим, что чем меньше погрешность  Если же необходимо, чтобы сглаживающий кубический сплайн прошел через точку
Если же необходимо, чтобы сглаживающий кубический сплайн прошел через точку  то соответствующий весовой множитель
то соответствующий весовой множитель  следует положить равным нулю. В практических вычислениях выбор величин
следует положить равным нулю. В практических вычислениях выбор величин  является важным вопросом, для решения которого используются различные подходы /9/.
является важным вопросом, для решения которого используются различные подходы /9/.
 и
и  Опишем алгоритм нахождения коэффициентов сплайна, для реализации которого требуется
Опишем алгоритм нахождения коэффициентов сплайна, для реализации которого требуется  арифметических действий и
арифметических действий и  с невырожденной пятидиагональной матрицей методом прогонки (п.п.1.2). Запишем эту систему линейных уравнений для случая равномерного шага и одинаковых значений весовых коэффициентов
с невырожденной пятидиагональной матрицей методом прогонки (п.п.1.2). Запишем эту систему линейных уравнений для случая равномерного шага и одинаковых значений весовых коэффициентов 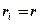



 мы получаем систему линейных уравнений с трехдиагональной матрицей (случай естественного интерполяционного кубического сплайна).
мы получаем систему линейных уравнений с трехдиагональной матрицей (случай естественного интерполяционного кубического сплайна). находим
находим  где
где  - это значения естественного сглаживающего кубического сплайна в узлах сетки,
- это значения естественного сглаживающего кубического сплайна в узлах сетки,  Значения
Значения 

 и
и  , которые потребуются для вычисления значения сплайна и его производных при
, которые потребуются для вычисления значения сплайна и его производных при 



