
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение коэффициентов интерполяционного
Параболического сплайна
Из определения интерполяционного параболического сплайна вытекает система линейных уравнений размерности
Отметим, что мы привели формулы для случая левого краевого условия Теорема (оценка погрешности). Пусть где Из оценки погрешности вытекает, что при уменьшении равномерного шага Производная интерполяционного параболического сплайна – это непрерывная кусочно-линейная функция, то есть линейный сплайн:
Нахождение значений интерполяционного параболического сплайна И его производной
Как и в случае линейного сплайна, сначала находим номер
Как и для линейного сплайна, введем дополнительные коэффициенты:
Сложность вычислительного алгоритма построения интерполяционного параболического сплайна. Число арифметических действий, необходимых для построения интерполяционного параболического сплайна, пропорционально числу отрезков ( Пример. Приведем текст программы, которая по интерполяционной таблице и левому краевому условию строит интерполяционный параболический сплайн
Программа #include <stdio.h> #include <conio.h> #include <math.h>
float A,B; //границы отрезка
float Xi[21],Yi[21]; //интерполяционная таблица float Ai[21],Bi[21],Ci[21]; //коэффициенты ai, bi, ci float h; //шаг сетки float n; //число отрезков float d1;
//Функция sin(x) float fn (float x) { return (sin(x)); }
//Производная функции sin(x) float fsh (float x) { return (cos(x)); }
//Вычисление значений сплайна S(x) float Sx (float x)
{ int i=int((x-A)/h); return Ai[i]+Bi[i]*(x-Xi[i])+Ci[i]*(x-Xi[i])*(x-Xi[i]); }
//Вычисление значений производной сплайна float Sshx (float x)
{ int i=int((x-A)/h); return Bi[i]+2*Ci[i]*(x-Xi[i]); }
void main() { clrscr(); float Ti=0; //вспомогательная переменная ti
//Инициализация начальных значений A=0; B=2; //отрезок [0,2] n=20; //число отрезков n h=float(B-A)/n; //шаг d1=1; //Создание интерполяционной таблицы for(int i=0;i<=n;i++)
{ Xi[i] = A+i*h; Yi[i] = fn(Xi[i]); }
//Находим коэффициенты сплайна ai, bi, ci //Расчет коэффициентов ai for(i=0;i<=n;i++) Ai[i]=Yi[i];
//Расчет коэффициентов Bi и ci Bi[0]=d1; for(i=0;i<=n-2;i++) { Bi[i+1]=2*(Yi[i+1]-Yi[i])/h-Bi[i]; Ci[i]=(Bi[i+1]-Bi[i])/(2*h); } Ci[n-1]=((Yi[n]-Yi[n-1])/(h*h))-Bi[n-1]/h; Ci[n]=Ci[n-1]; Bi[n]=Bi[n-1]+2*Ci[n-1]*h;
//Вывод результатов на печать
printf("Значение функции f в точке x=%.2f равно %.5f\n",0.15,fn(0.15)); printf("Значение сплайна P в точке x=%.2f равно %.5f\n",0.15,Sx(0.15)); printf("Значение производной функции f' в точке x=%.2f равно %.4f\n",0.15,fsh(0.15)); printf("Значение производной сплайна P' в точке x=%.2f равно %.4f\n",0.15,Sshx(0.15)); getch();
} Результат работы программы
Значение функции f в точке x=0.15 равно 0.14943 Значение сплайна P в точке x=0.15 равно 0.14945 Значение производной функции f'в точке x=0.15 равно 0.9887 Значение производной функции P'в точке x=0.15 равно 0.9883
2.3. Интерполяционный кубический сплайн
Наиболее часто на практике используется интерполяционный кубический сплайн. Кубический сплайн - это дважды непрерывно дифференцируемая функция, состоящая из «кусочков» полиномов третьей степени. Обозначим
где Так как
Определение. Кубический сплайн, удовлетворяющий краевым условиям Сформулируем определение естественного интерполяционного кубического сплайна. Определение естественного интерполяционного кубического сплайна. Пусть на отрезке 1) функция 2) на каждом из отрезков
3) функция 4) краевым условиям Отметим, что, отбросив условие три, мы получаем определение естественного кубического сплайна. Пример. Функция
является естественным кубическим сплайном, определенным на отрезке
Пример программы, которая по интерполяционной таблице строит естественный интерполяционный кубический сплайн, приводится в примере выполнения задания 2 расчетно-графического задания 1. Теорема существования и единственности. Пусть на отрезке Другими словами, если задана интерполяционная таблица, в которой все узлы сетки различны, то существует единственный естественный интерполяционный кубический сплайн, удовлетворяющий этой таблице.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.240.243 (0.046 с.) |
 относительно неизвестных
относительно неизвестных  ,
,  и
и  ,
, 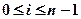 . Эта система линейных уравнений имеет единственное решение, если все узлы сетки различны. Система линейных уравнений легко решается, и мы можем записать следующие явные формулы для нахождения коэффициентов
. Эта система линейных уравнений имеет единственное решение, если все узлы сетки различны. Система линейных уравнений легко решается, и мы можем записать следующие явные формулы для нахождения коэффициентов  ,
,  ;
; ,
,  ,
,  ;
; .
. . Для правого краевого условия
. Для правого краевого условия  формулы записываются аналогично.
формулы записываются аналогично. . Тогда для любой точки
. Тогда для любой точки 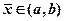 справедлива следующая оценка погрешности:
справедлива следующая оценка погрешности:  ,
,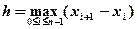 , положительная константа
, положительная константа  не зависит от
не зависит от 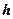 .
. ,
, 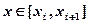 ,
,  отрезка, содержащего точку
отрезка, содержащего точку  , по формуле
, по формуле  . Зная все коэффициенты
. Зная все коэффициенты  в точке
в точке  ,
, .
. ,
, 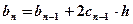 ,
,  . Эти коэффициенты потребуются для вычисления
. Эти коэффициенты потребуются для вычисления  в точке
в точке  . Значение производной интерполяционного параболического сплайна в точке
. Значение производной интерполяционного параболического сплайна в точке  .
. ), объем памяти также пропорционален числу отрезков (
), объем памяти также пропорционален числу отрезков (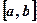 ,
,  с равномерным шагом
с равномерным шагом  , где
, где  . Узлы сетки вычисляются по формуле
. Узлы сетки вычисляются по формуле  , где
, где 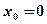 ,
,  , значения
, значения  находятся по формуле
находятся по формуле  Задано краевое условие
Задано краевое условие  . На печать выдаются значения интерполяционного параболического сплайна
. На печать выдаются значения интерполяционного параболического сплайна  производной интерполяционного параболического сплайна
производной интерполяционного параболического сплайна  в точке
в точке  .
. кубический сплайн. Для каждого
кубический сплайн. Для каждого 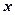 из отрезка
из отрезка 
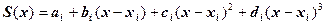 ,
, - числовые коэффициенты. Таким образом, на каждом отрезке
- числовые коэффициенты. Таким образом, на каждом отрезке  четыре неизвестных коэффициента:
четыре неизвестных коэффициента:  . Следовательно, нам требуется
. Следовательно, нам требуется  уравнения получаем из условий
уравнения получаем из условий 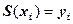 ,
,  . Во всех внутренних узлах сетки (число внутренних узлов равно
. Во всех внутренних узлах сетки (число внутренних узлов равно  ) функция
) функция  условий. В сумме получаем
условий. В сумме получаем  линейных уравнений. Два недостающих условия – это краевые (граничные) условия. Для кубических сплайнов рассматриваются четыре типа краевых условий, в дальнейшем мы будем рассматривать краевое условие вида
линейных уравнений. Два недостающих условия – это краевые (граничные) условия. Для кубических сплайнов рассматриваются четыре типа краевых условий, в дальнейшем мы будем рассматривать краевое условие вида .
. , в узлах которой заданы значения
, в узлах которой заданы значения 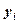 ,
, 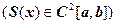 ;
;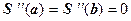 .
.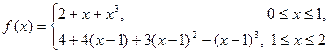
 . Эта же функция является естественным интерполяционным кубическим сплайном, удовлетворяющим следующей интерполяционной таблице:
. Эта же функция является естественным интерполяционным кубическим сплайном, удовлетворяющим следующей интерполяционной таблице:
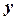
 ,
,  при
при 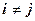 ). Тогда существует единственный естественный кубический сплайн
). Тогда существует единственный естественный кубический сплайн 


