
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 23. дифференциальная функция распределения ⇐ ПредыдущаяСтр 4 из 4
Плотность вероятности непрерывной случайной величины, она же дифференциальная функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией (многоугольник распределения), то плотность вероятностей графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Аналитически задаётся формулой.
Вопрос 25. дисперсия Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/ k ². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
Определение Пусть
где символ [Замечания § Если случайная величина
§ Дисперсия является вторым центральным моментом случайной величины; § Дисперсия может быть бесконечной. См., например, распределение Коши. § Дисперсия может быть вычислена с помощью производящей функции моментов
§ Дисперсия целочисленной случайной величины может быть вычислена с помощью производящей функции последовательности. Свойства Дисперсия любой случайной величины неотрицательна:
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.189 (0.004 с.) |

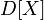 в русской литературе и
в русской литературе и  (англ. variance) в зарубежной. В статистике часто употребляется обозначение
(англ. variance) в зарубежной. В статистике часто употребляется обозначение  или
или  . Квадратный корень из дисперсии, равный
. Квадратный корень из дисперсии, равный  , называетсясреднеквадрати́чным отклоне́нием
, называетсясреднеквадрати́чным отклоне́нием — случайная величина, определённая на некотором вероятностном пространстве. Тогда
— случайная величина, определённая на некотором вероятностном пространстве. Тогда
 обозначает математическое ожидание[1][2].
обозначает математическое ожидание[1][2].
 :
:
 Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; Если случайная величина равна константе, то её дисперсия равна нулю:
Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; Если случайная величина равна константе, то её дисперсия равна нулю:  Верно и обратное: если
Верно и обратное: если  то
то  почти всюду; Дисперсия суммы двух случайных величин равна:
почти всюду; Дисперсия суммы двух случайных величин равна: , где
, где  — их ковариация; Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:
— их ковариация; Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство: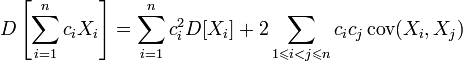 , где
, где  ; В частности,
; В частности,  для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;
для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;





