
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые выражения, его значение.
Любое число уже является числовым выражением. Если А и В -числовые выражения, то А + В, А - В, А • В, А: В также являются числовыми выражениями. Итак, в числовые выр-я входят лишь числа, знаки операций и скобки. пример: 46 (да), (24+13)x3 (да), 25+в (нет) Числовые выражения составляются из чисел с помощью знаков действий и скобок 13 - (23 - 63) * 2 не будут являться числовыми выражениями. Следует понимать, что одно число тоже будет являться числовым выражением. В нашем примере, это число 13. А, например, следующие записи · 100 - *9, · /32)343 · (*5 ·:) не будут являться числовыми выражениями, так как они лишены смысла и являются просто набором чисел и знаков. Значение числового выражения Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия. Например, (100-32)/17 = 4, то есть для выражения (100-32)/17 значением этого числового выражения будет являться число 4. 2*4+7=15, число 15 будет являться значением числового выражения 2*4+7. Часто для краткости записи не пишут полностью значение числового выражения, а пишут просто "значение выражения", опуская при этом слово «числового».
При вычислении значений числовых выражений следуют руководствоваться следующими правилами. 1. Если выражение не имеет скобок, то надо выполнять действия начиная с высших ступеней: третья ступень, вторая ступень и первая ступень. Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право. 2. Если в выражении присутствуют скобки, то сначала выполняются действия в скобках, а лишь затем все стальные действия в обычном порядке. При выполнении действий в скобках, если их там несколько, следует пользоваться порядком описанным в пункте 1.
3. Если выражение представляет собой дробь, то сначала вычисляются значении в числителе и знаменателе, а потом числитель делится на знаменатель. 4. Если в выражении присутствуют вложенные скобки, то выполнять действия следует с внутренних скобок. 22. Числовые равенства, их свойства. Если 2 числ-х выр-я соединить знаком равенства, то получим высказывание называемое числовым равенством. Числовое равенства могут быть истинным «и», ложным «л». Числовые рав-ва явл. истинными, если значение числовых выражений стоящих в левой и в правой частях равны. Св-ва числ. равенств. Рефлективность, симметричность, транзитивность. Если два числовых выражения записаны через знак равно, то эти выражения образуют числовое равенство. Например, выражение 2*4+7=15 является числовым равенством. Как уже отмечалось выше, в числовых выражениях могут использоваться скобки. Как уже известно скобки влияют на порядок действий. Вообще, все действия разделены на несколько ступеней. Действия первой ступени: сложение и вычитание. Действия второй ступени: умножение и деление. Действия третей ступени – возведение в квадрат и возведение в куб. 23. Числовые неравенства, их свойства. Если два числовых выр-я соеденины знаком < или >, то получится высказывание, которое называется числовым неравенством. Если a > b, то b < a Если a > b и b > c, то a > c (свойство транзитивности) Если a > b, то a + c > b + c Если a > b и c > 0, то ac > bc Если a > b и c < 0, то ac < bc Если a > b и c > d, то a + c > b + d Если a, b, c, d > 0, причём a > b и c > d, то ac > bd Если a > b и c < d, то a – c > b – d Если a > b > 0, то Если a > b > 0, то для любого натурального числа n справедливо неравенство а>в (в n степени) 1) Числовое неравенство – запись отношений двух неравных чисел с помощью знаков > или<. 2) Число а больше числа в, если разность а-в– положительное число; число а меньше числав, если разность а-в – отрицательное число. 3) Правила перехода от одних неравенств к другим называются свойствами неравенств. 4) 4 свойства числовых неравенств: 1 свойство: если первое число больше второго, то второе число меньше первого; 2 свойство: если первое число меньше второго, а второе меньше третьего, то первое число меньше третьего;
3 свойство: к обеим частям неравенства можно прибавить одно и то же число; 4 свойство: обе части неравенства можно умножить (или разделить) на одно и то же положительное число; оставив знак неравенства без изменения. Обе части неравенства можно умножить (или разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
24.Выражение с переменными, его область определения Если числовое выражение содержит и буквы, то мы имеем выражение с переменными. Например, 2а - 3; За + 2b с + 8. Выражение с переменными обычно обозначают так: f(х); А(b;с); В(х;у) Если в выражение с переменными подставить вместо букв их значения, то получится числовое выражение.Те значения переменной, при которых выражение с переменной имеет числовое значение, называется областью определения выражения с переменной. Например, областью определения выражения с переменной 2а - 3 на множестве действительных чисел является все множество действительных чисел, а на множестве натуральных чисел - натуральные числа, начиная с двух (если а = 1, то 2 • 1 - 3 не является натуральным числом). Запись из чисел, букв, знаков действий и скобок. Например, Переменная - это буква, входящая в буквенное выражение. Переменная может принимать любые числовые значения. Числовое значение выражения с переменной зависит от значения переменной. Область определения Множество значений переменных, при которых выражение с переменной имеет смысл, называется областью определения этого выражения. Например, выражение
25. Понятие тождественного преобразования выражений. Определение тождества. Равенство, верное при любых значениях переменных, называется тождеством. Тождеством считают и верные числовые равенства. Тождествами также являются равенства, выражающие основные свойства действий над числами: a + b = b + a ab = ba (a + b) + c = a + (b + c) (ab)c = a(bc) a(b + c) = ab + ac Тождественные преобразования Замену одного выражения другим, тождественно равным ему выражением называют тождественным преобразованием или просто преобразованием выражения. Тождественные преобразования выражений с переменными выполняются на основе основный свойств действий над числами. Тождественные преобразования выражений широко применяются при вычислении значений выражений и решении других задач. Некоторые тождественные преобразования Вам уже приходилось выполнять, например приведение подобных слагаемых и раскрытие скобок.Напомним правила выполнения этих преобразований: чтобы привести подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную часть если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки 26. Определение модуля. Алгоритмтождественного преобразования выражений с модулем. Модулем числа называется расстояние от начала отсчёта до точки, изображающей это число на координатной прямой. Иногда вместо термина «модуль» используется термин «абсолютная величина» или «абсолютное значение» числа. Обозначается модуль посредством символа ││. В соответствии с приведенным определением: │5│=5, │-3│=3, │0│=0. Обратите внимание: модуль числа всегда неотрицателен: |a|≥ 0. Определение модуля:
При работе с модулями используют различные свойства модулей, например:
27.Деление многочлена на многочлен (пример)
2) Умножаем полученное выражение 4a на делитель 4a² – a + 2; записываем результат 16a³ – 4a² + 8a под делимым (один подобный член под другим). 3) Вычитаем почленно этот результат из делимого и сносим вниз следующий по порядку член делимого 7; получаем остаток 12a² –13a + 7. 4) Делим первый член 12a² этого выражения на первый член 4a² делителя; результат 3 – это второй член частного. 5) Умножаем этот второй член частного 3 на делитель 4a² – a + 2 и вновь записываем результат 12a² – 3a + 6 под делимым (один подобный член под другим). 6) Вычитаем почленно полученный результат из предыдущего остатка и получаем второй остаток: – 10a + 1. Его степень меньше степени делителя, поэтому деление заканчивается В результате получили частное 4a + 3 и остаток –10 a + 1.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1888; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.014 с.) |

 имеет смысл при любом значении x, кроме 7. Если x=7, получим деление на ноль. Область определения - это множество всех чисел, кроме 7.
имеет смысл при любом значении x, кроме 7. Если x=7, получим деление на ноль. Область определения - это множество всех чисел, кроме 7.





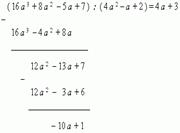 1) Делим первый член 16a³ делимого на первый член 4a² делителя; результат 4a является первым членом частного.
1) Делим первый член 16a³ делимого на первый член 4a² делителя; результат 4a является первым членом частного.


