
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потоки Эрланга, их свойства и применение.
Потоком Эрланга k-го порядка называется поток Пальма, у которого интервалы времени между событиями распределены по закону Эрланга k-го порядка. Поток Эрланга k-го порядка может быть получен из простейшего с помощью его прореживания. В простейшем потоке сохраняется каждое k-е событие, остальные отбрасываются. Привести схему формирования: Интервал между соседними событиями в потоке Эрланга 3-го порядка – сумма трех независимых СВ, имеющих показательное распределение с параметром
Поток Эрланга k-го порядка
Функция плотности распределения интервала времени между двумя событиями
Числовые характеристики СВ Математическое ожидание длины интервала времени между последовательными моментами поступления событий:
Дисперсия интервала времени между последовательными моментами поступления событий:
Свойства потока Эрланга. При k= 1получается обычное экспоненциальное распределение, а при + все свойства простейшего потока: стационарность, ординарность. 9.2. Марковский случайный процесс Второе понятие, которое часто используют при моделировании систем – это понятие случайного процесса. Пусть имеется некоторая система S, которая в процессе функционирования может принимать различные состояния Si, i=1..n. Если состояния системы меняются случайным образом, то последовательность состояний системы образует случайный процесс. Различают системы с непрерывным и дискретным временем. Системы с непрерывным временем предполагают, что переход системы из одного состояния в другое может осуществляться в любой момент времени, т. е. время пребывания системы в каждом состоянии представляет непрерывную случайную величину. Для систем с дискретным временем время пребывания системы в каждом состоянии фиксированное, а моменты переходов t1, t2,..., tk размещаются на временной оси через равные промежутки и называются "шагами" или "этапами". Время нахождения системы в некотором состоянии представляет дискретную случайную величину. Полное множество состояний Si исследуемой системы может быть либо конечным (i = 1, n), либо бесконечно большим. Большинство реальных систем имеют дискретное конечное пространство состояний. Последовательность состояний такой системы Si (i = 1, n) и сам процесс переходов из состояния в состояние называется цепью.Дискретные цепи Маркова
Пусть имеется система S с дискретными состояниями s1, s2, …, sn. Процесс, протекающий в системе S, называется Марковским процессом с дискретными состояниями и дискретным временем (или дискретной Марковской цепью), если выполняется условие: для любого фиксированного момента времени (любого шага) условные вероятности состояния системы в будущем зависят только от состояния системы в настоящем и не зависят от того, когда (на каком шаге) и откуда система перешла в это состояние. Например, рассматривается процесс: система представляет техническое устройство, которое осматривается в определенные моменты времени (например, через сутки) и ее состояние регистрируется. Каждый осмотр – шаг процесса. Возможные состояния следующие: s1 – полностью исправно; s2 – частично исправно, необходима наладка; s3 – серьезная неисправность, требует ремонта; s4 – непригодно. Основной задачей исследования Марковской цепи является нахождение безусловных вероятностей нахождения системы S на любом шаге k в состоянии si. Непрерывные цепи Маркова На практике Марковские процессы с дискретным состоянием и дискретным временем встречаются довольно редко. Как правило, рассматривают Марковские случайные процессы с дискретными состояниями и непрерывным временем. Пусть имеется некоторая система S, переходы системы из состояния в состояние происходят в случайные моменты времени. Переходы системы из состояния в состояние происходят под воздействием каких-либо потоков событий (например, «поток отказов», поток восстановлений). Для системы такими событиями могут быть:
- поступление очередной заявки в СМО (систему массового обслуживания) (событие входного потока); - окончание обслуживания очередной заявке (событие потока обслуживании заявок), и т.д. Процесс, протекающий в системе S, называется Марковским процессом с дискретными состояниями и непрерывным временем (или непрерывной Марковской цепью), если выполняется условие: для любого фиксированного момента времени условные вероятности состояния системы в будущем зависят только от состояния системы в настоящем и не зависят от того, когда (на каком шаге) и откуда система перешла в это состояние. Схематично СМО удобно представлять в виде размеченного графа состояний Пусть Например, рассматриваемая система – компьютер, обрабатывающий поток заданий. В очереди на обработку может стоять не более двух заданий. Поток заданий Пуассоновский с интенсивностью
- в системе 2 заявки, компьютер работают и одна заявка в очереди;
Граф состояний – схема, отражающая переход системы из состояния в состояние.
Вершины графа соответствуют состояниям, дуги – переходам из состояния в состояние. Размеченный граф состояний - граф состояний с проставленными у стрелок интенсивностями соответствующих потоков событий, переводящих систему из состояния в состояние. Здесь и в дальнейшем предполагается ординарность суммарного потока всех событий в СМО, то есть одновременно не могут произойти два и более событий. В данной СМО одновременно невозможно окончание обслуживание и поступление на вход СМО заявки. Другим предположением является нулевое время перехода заявки из очереди на канал обслуживания и момент его освобождения. Можно доказать, что если все потоки событий, переводящие систему из состояния в состояние пуассоновские и независимые, то процесс, протекающий в системе – Марковский. Обозначим
так как события, состоящие в том, что в момент t система S находится состояниях Оказывается, зная размеченный граф состояний, можно определить вероятности состояний как функцию времени. А именно, эти вероятности удовлетворяют определенного вида дифференциальным уравнениям, называемым уравнениями Колмогорова. Решая эти уравнения, мы получим искомые вероятности. Общее правило составления дифференциальных уравнений, справедливое для любой непрерывной марковской цепи. В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, то соответствующий член имеет знак «минус»;если стрелка направлена в состояние - знак «плюс». Каждый член равен произведению интенсивности потока событий, соответствующего данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.
Для примера, рассмотренного выше, система уравнений Колмогорова будет иметь вид:
Уравнение для последнего состояния (или одного из состояний) не составляется, а заменяется нормировочным условием.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.254.0 (0.01 с.) |
 .
. .
. .
. для СВ
для СВ 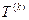 имеет вид:
имеет вид: - закон Эрланга k-го порядка.
- закон Эрланга k-го порядка.
 .
. поток Эрланга приближается к регулярному потоку с постоянным интервалом между событиями (M). Это свойство потоков Эрланга удобно в практических применениях: оно дает возможность, задаваясь различными k, получать потоки, обладающие различным последействием - от полного отсутствия последействия (к=1), до жесткой функциональной связи между моментами появления событий (
поток Эрланга приближается к регулярному потоку с постоянным интервалом между событиями (M). Это свойство потоков Эрланга удобно в практических применениях: оно дает возможность, задаваясь различными k, получать потоки, обладающие различным последействием - от полного отсутствия последействия (к=1), до жесткой функциональной связи между моментами появления событий ( ).
).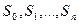 - совокупность возможных состояний системы.
- совокупность возможных состояний системы. .
.
 - в системе нет ни одной заявки, компьютер простаивают;
- в системе нет ни одной заявки, компьютер простаивают; - в системе одна заявка, компьютер работает;
- в системе одна заявка, компьютер работает;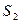
 - в системе 3 заявки, компьютер работают и две заявки в очереди
- в системе 3 заявки, компьютер работают и две заявки в очереди
 - вероятность того, что в момент t система будет находиться в состоянии
- вероятность того, что в момент t система будет находиться в состоянии  (
( ). Очевидно, для любого момента t сумма вероятностей состояний равна единице:
). Очевидно, для любого момента t сумма вероятностей состояний равна единице:
 , которые несовместны и образуют полную группу.
, которые несовместны и образуют полную группу.



