
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гюгенс штейнер. Макроскопиялық параметрлердің. Газ молекулаларының жылдамдықтар бойынша үлестірілудің максвелл теңдеуі
43 Ван дер ваальс Нақты газдар. Бойл-Мариот және Гей-Люссак заңдарына бағынбайтын газдар.Нақты газдардың молекуларының өлшемдері болады және олар бір-бірімен өзара әсерлеседі.Нақты газдардың күйін анықтайтын теңдеуді алу үшін голланд ғалымы Ван-дер-Ваальс Менделеев-Клапейрон теңдеуіне молекулаларды өлшемдерін және өзара әсерлесуін ескеретін түзету енгізді. Бұл алынған теңдеу нақты газдардың күй теңдеуі немесе Ван-дер-Ваальс теңдеуі деп аталады. Мөлшері 1 моль нақты газ үшін Ван-дер-Ваальс теңдеуі келесі түрде жазылады: ГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГГ 15. ГЮГЕНС штейнер Біреуі массалар центрі арқылы өтетін өзара параллель өстерге қатысты дененің инерция моменттерінің арасындағы тәуелділікті Гюйгенс-Штейнер теоремасы береді: дененің кез келген өске қатысты инерция моменті берілген өске параллель оның массалар центрі арқылы өтетін өске қатысты инерция моменті мен дене массасының өстер арасындағы қашықтық квадратына көбейтіндісінің қосындысына тең (дәлелдеусіз).
Сонымен, Гюйгенс-Штейнер теоремасы былай жазылады:
27. Макроскопиялық параметрлердің (қысым, көлем) микроскопиялық параметрлермен (молекулалардың массасы, жылулық қозғалыс жылдамдығы, кинетикалық энергиясы) арасындағы байланысты көрсететін өрнекті молекула-кинетикалық теорияның негізгі теңдеуі деп атайды. МКТ - нің негізгі қағидалары: 1. Барлық денелер микробөлшектерден тұрады. 2. Денедегі микробөлшектер үздіксіз және хаосты қозғалыста болады. 3. Денедегі микробөлшектер өзара әрекеттеседі.
v- орташа кВ жылдамдық
R-8.31 универсал газ 28. Газ молекулаларының жылдамдықтар бойынша үлестірілудің Максвелл теңдеуі Ағылшын ғалымы Максвелл газ молекулаларының жылдамдық бойынша таралып орналасуын анықтайтын заңды ашты. Бұл заңдылық Максвелл таралуы деп аталды.
Максвелл ықтималдық теориясы мен математикалық статистика заңдылықтарын пайдалана отырып таралу функциясын алды. Таралу функциясы Газ молекулаларының жылдамдықтар бойынша таралу графигі келесі суретте көрсетілген. Газдарды қыздырғанда аз жылдамдықпен қозғалатын молекулалардың үлесі азаяды, ал үлкен жылдамдықпен қозғалатын молекулалардың үлесі артады. Газдағы көпшілік молекулалар ықтимал жылдамдықтай жылдамдықпен қозғалады. Молекулалардың орташа жылдамдығы - Молекулалардың орташа квадраттық жылдамдығы - Яғни осы формулалардан 30.Газ молекулаларының ретсіз қозғалысы Молекулалардың ретсіз қозғалысын жылулық қозғалыс деп атаймыз. Жылулық қозғалыстағы газ молекулалары бір-бірімен үздіксіз соқтығысады. Соқтығысқанша олар l жолды еркін жүреді. Еркін жүру жолы – кездейсоқ шама Газ молекуласының көршілес екі соқтығысу арасында жүріп өткен ара қашықтығын газ молекуласының еркін жолының ұзындығы деп атайды. Өлшем бірлігі
Соқтығысулардыц орташа санын (z) табу үшін, қарастырылып отырған молекуладан басқа молекулалардың барлығы аз орындарында қозғалмайды деп ұйғарамыз. Соқтығысудың нәтижесінде молекула өзінің ұшу бағытын өзгертіп, радиусы r цилиндрдің ішінде орналасқан басқа молекуламен кездескенше түзу сызықты қозғалады (4-сурет). 1 секунд ішінде молекула u-ға тең жол жүреді. Осы уақыттың ішінде тыныш тұрған молекулалармен соқтығысу санының ұзындығы u, радиусы r және көлемі V=πd2u болатын цилиндрдің ішінде қалатын молекулалардың санына тең болады. Осы көлемді бірлік көлемдегі молекулалар саны п0-ге көбейтіп, қозғалыстағы молекуланың 1 секунд ішінде қозғалмай тұрған мо- лекулалармен соқтығысуларынын орташа санын табамыз: z=πd2un0 Басқа молекулалар да қозғалыста болатындықтан, соқтығысудың z саны (9) формулада көрсетілген мәнінен басқаша, яғни z-тің мәніне
Мұндағы d — соқтығысу кезінде екі молекула центрлерінің арасын- дағы ен аз қашыктықтағы молекуланың эффективті диаметрі деп аталады. 34. Газ молекулаларының еркіндік дәрежелер саны Газ молекуласының еркіндік дәрежесі деп молекуланың кеңістіктегі орнын анықтайтын тәуелсіз параметрлердің жиынтығын айтамыз. Егер кез-келген дене кеңістікте қозғалатын болса, онда осы қозғалысты тәуелсіз алты қозғалыстың жиынтығы түрінде қарастыруға болады: үш ілгерілемелі қозғалыстың (тікбұрышты координаталар жүйесінің осьтері бойымен), үш айналмалы қозғалыстың (дененің массалар центрі арқылы өтетін өзара перпендикуляр үш осьтің айналасында) жиынтығы. Қалыпты жағдайда газ молекулаларының еркіндік дәрежесі: Бір атомды газ үш бағытта ілгерілемелі қозғала алады. Сондықтан бір атомды газдың еркіндік дәрежесі 3 -ке тең. Екі атомды газ үш бағытта ілгерілемелі және екі бағытта айналмалы қозғала алады (сурет). Сондықтан екі атомды газдың еркіндік дәрежесі 5 -ке тең болады.
Ішкі энергия өзгерісі – берілген газ массасы үшін температураның өзгерісінен ішкі энергиясы өзгереді dU=U2-U1 Идеал газдардың iшiнде өзiнiң физикалық қасиеттерi бойынша қарапайым болып табылатын газ — бiр атомды газ (гелий, неон, аргон және т.б.). Бiр атомды газдың iшкi энергиясы. Идеал газдың барлық iшкi энергиясы оның молекулаларының қалыптаспаған қозғалысының кинетикалық энергиясы болып табылады. Массасы m бiр атомды газ үшiн ол бiр атомның орташа кинетикалық энергиясының E = 3kT/2 жалпы атомдар санына N = mNa/M көбейткенге тең. kNa = R екенiн ескерiп, мынаны табамыз: U = 3mRT/2M. 37. Газдардың жылусыйымдылығы Заттың жылу сыйымдылығы деп заттың температурасын 1 Кельвинге өзгертуге қажетті жылу мөлшерін айтады. Өлшем бірлігі – Дж/К. Заттың жылу сыйымдылықтары денені қыздыру әдісіне тәуелді болады. Денені қыздыру тұрақты көлемде жүретін болса, онда жылу сыйымдылығын тұрақты көлемдегі жылу сыйымдылығы деп атайды. Ал егер қыздыру тұрақты қысымда жүретін болса, онда жылу сыйымдылығын тұрақты қысымдағы жылу сыйымдылығы деп атайды. Мольдік жылу сыйымдылығы деп мөлшері бір моль заттың температурасын бір Кельвинге өзгертуге қажетті жылу мөлшерін айтады. Өлшем бірлігі – Дж/моль.К.
Изохоралық процесс. Изохоралық процесс кезінде газ жұмыс нольге тең және жүйеге берілген жылу мөлшері жүйенің ішкі энергиясын өзгертуге жұмсалады. Ішкі энергия өзгерісі мұндағы:
Изобаралық процесс. P=const Изобаралық процесс кезінде термодинамиканың жүйеге берілген жылу мөлшері жүйенің ішкі энергиясын өзгертуге және жүйенің сыртқы денелермен жұмыс атқаруына жұмсалады: Жүйеге берілген жылу мөлшері: мұндағы:
Газдың тұрақты қысымдағы және тұрақты көлемдегі мольдік жылу сыйымдылықтарының айырмасы универсал газ тұрақтысына тең. Cp тұрақты қысымдағы мольдік жылу сыйымдылығы әрқашан CV тұрақты көлемдегі мольдік жылу сыйымдылығынан үлкен болады Идеал газдың изобаралық және изохоралық процестеріндегі меншікті жылу сыйымдылықтарының арасындағы байланыс: -тұрақты қысым кезіндегі мольдік жылу сыйымдылық. -тұрақты көлем кезіндегі мольдік жылу сыйымдылық.
-Майер формуласы.
45. Гармоникалаық тербелістер Шамалары уақыт бойынша косинус н/е синус заңы бойынша өзгеретін тербелістер.
Еркін тербелістер жүйе тепе-теңдік жағдайынан шығарылған кездегі жүйедегі ішкі күштердің әсерінен болады. Еркін тербелістер гармоникалық болуы үшін тербелмелі жүйенің сызықты болуы керек, және мұнда энергия диссипациясы болмауы қажет. Еріксіз тербелістер сыртқы периодты күштер әсерінен болып тұрады. Олар гармоникалық болуы үшін тербелмелі жүйенің сызықты болуы, ал сыртқы күштер өздері уақыт өткен сайын гармоникалық түрде өзгеріп тұруы қажет. Гармоникалық тербелістердің жалпы дифференциалдық түрі:
v=dx/dt=- a=dv/dt=- ИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИИ Импульс моменті Импульс моменті, "Қозғалыс мөлшері моменті" деп те аталады, – материалдық нүктенің немесе жүйенің механикалық қозғалысының динамикалық сипаттамаларының бірі. Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Тұйықталған жүйенің материялық нүктелерінің (денелер) толық импульс моменті тұрақты болып қалады. Импульс моментінің сақталу заңы да импульстің сақталу заңы сияқты табиғаттың негізгі заңы болып табылады. Оның негізінде кеңістіктің изотроптылығы қасиеті жатыр, яғни тұйық жүйенің бұрылуы оның механикалық қасиеттеріне әсер етпейді.
Идеал газ Идеал газ – бөлшектерінің өзара әсері ескерілмейтін газдың теориялық моделі. Ол классикалық идеал газ және кванттық идеал газ болып ажыратылады. Классикалық идеал газдың қасиеттері классикалық физика заңдарымен – Клапейрон теңдеуімен, сондай-ақ оның дербес түрлері Бойль–Мариотт заңы және Гей-Люссак заңымен сипатталады. Параметрлердің біреуінің мәні өзгермей қалған кезде өтетін процес ер изопроцестер деп аталады. Изобаралық процесс. Қысым тұрақты болғанда, термодинамикалық жүйе күйінің өзгеруі процесі изобаралық( Гей –Люссак ) деп аталады. Егер газ қысымы өзгермесе, берілген массалы газ үшін көлемнің температураға қатысы тұрақты болады.
Р =const Изохорлық процесс. Көлем тұрақты болғанда термодинамикалық жүйе күйінің өзгеру процесі изохоралық (Ж.Шарль) деп аталады. V =const Изотермиялық процесс. Температура тұрақты болғанда мак-роскопиялық, денелердің термодинамикалық, жуйесі күйінің өзгеру процесін изотермиялық(Бойль — Мариотт) депатайды.м 27.Идеал газдың молекула кинетикалық теориясы МКТ Макроскопиялық параметрлердің (қысым, көлем) микроскопиялық параметрлермен (молекулалардың массасы, жылулық қозғалыс жылдамдығы, кинетикалық энергиясы) арасындағы байланысты көрсететін өрнекті молекула-кинетикалық теорияның негізгі теңдеуі деп атайды. МКТ - нің негізгі қағидалары: 1. Барлық денелер микробөлшектерден тұрады. 2. Денедегі микробөлшектер үздіксіз және хаосты қозғалыста болады. 3. Денедегі микробөлшектер өзара әрекеттеседі.
v- орташа кВ жылдамдық
R-8.31 универсал газ
ККККККККККККККККККККККККККККККККККККККККККККККККК 9. Кинетикалық және потенциалдық энергия Механикалық жүйенің кинетикалық энергиясы
Кинетикалық энергия дене қозғалысының өлшемі болып, ол дене басқа денелермен әсерлескенде жасалатын жұмыс шамасын анықтайды. Потенциалдық энергия – жүйе бөлшектерінің өзара орналасуы мен олардың сыртқы күш өрістерінде орналасуына байланысты болатын жүйенің механикалық энергиясының бір түрі. Денелер жүйесінің бір-біріне байланысты орын ауыстыруы нәтижесінде пайда болатын жүйенің потенциалдық энергиясының өзгеруі сыртқы немесе ішкі күштер әсерінен пайда болады. Демек, потенциалдық энергияның өзгеруі жүйенің жылдамдығын өзгертпей оны бір орыннан екінші орынға ауыстырудағы консервативті күштердің жұмысына тең. Шамалары тек қана өзара әсерлесетін денелердің ара қашықтығына тәуелді күштердің консервативті екендігін дәлелдеуге болады. Мысалы, жүйелердің ішкі күштері: ауырлық күші Егер жүйедегі денелерге қозғалу мүмкіндігін берсе, онда дене ішкі күштердің әсерінен жұмыс жасайды, ал ол жұмыс жүйенің потенциалдық энергиясы болады: 1) массасы 2)
3) Бір-бірінен
4)Бір-бірінен
17.Күш моменті Айналу осі бар денелердің тепе-теңдік шартын анықтау үшін күш моменті деген ұғым енгізіледі.Түсетін күштің өз күш иініне көбейтіндісі күш моменті деп аталады. М = F*d M=F×dM=күшмоменті; F=күш;d=күшиіні Н*м Қатты дененің айнымалы қозғалысы деп осы дене қозғалыста болғанда дененің екі нүктесі бастапқы орынын өзгертпейтін жағдайды айтамыз және осы екі нүктеден өтетін ось айналу осі депаталады.
26. Клапейрон – Менделеев теңдеуі Клапейрон – Менделеев теңдеуі – идеал газдың күйін анықтайтын және оның негізгі параметрлерінің (p қысымның, V көлемнің және T абсолют температураның) арасындағы байланысты тағайындайтын теңдеу.
Заттың мольдік массасы - бір мольдің мөлшерінде алынған заттың массасы. Заттың мөлшері v берілген денедегі N молекулалар санының NА Авогадро тұрақтысына, яғни заттың 1 моліндегі молекулалар санының катынасына тең. 36. Көлемнің өзгеруі Термодинамикадағы жұмыс – газбен жұмыс істегенде оның әр уақытта көлемі өзгереді: ΔV=V2-V1 A=PΔv A=P(v2-v1) Газ тек көлемі өзгергенде жұмыс атқарады. Егер газдың көлемі ұлғайса, газ оң жұмыс атқарады, ал газ сығылса (көлемі азайса) теріс жұмыс атқарады. Егер газдың қысымы тұрақты болса, онда газдың көлемі v1-ден v2-ге өзгергенде атқарылатын жұмыс A=P(v2-v1) өрнегімен анықталады. Термодинамикадағы 2 түрлі жұмыс: Газдың жұмысы: A^ газ ұлғайса Сыртқы күщтержің жұмысы: А газ сығылса Термодинамикадағы жұмыс P(v) графигі астындағы фигураның ауданына тең:
51. кулон заңы. Электр тұрақтысы. Ортаның диэлектрлік өтімділігі. Кулон заңы Нүктелік зарядтардың өзара әсерлесуінің негізгі заңын, тәжірибе жүзінде Кулон анықтады. Кулон заңын тұжырымдамас бұрын нұктелік заряд ұғымын енгіземіз (кинематикада енгізілген материялық нүкте туралы түсінік сияқты) нүктелік заряд дегеніміз – сызықтық өлшемдері әсерлесуші зарядталған денелердің ара қашықтығынан өте аз болып келетін денеде орналасқан заряд. Кулон заңы бойынша: вакуумда орналасқан екі
мұндағы
мұндағы
мұндағы
Бұл формуладағы
мұндағы 60. конденсаторлар. Жазық, цилиндрлік, сфералық конденсаторлардың эл сыйымдылығы Бір-бірінен диэлектрик қабатымен бөлінген екі металл пластинадан тұратын электрлік жүйені конденсатор деп аталады. Металл пластиналар конденсатор астарлары деп аталады. Конденсаторлар жазық, сфералық, цилиндрлік болып бөлінеді.
1) Жазық конденсатор
Зарядтардың беттік тығыздығы 2) Сфералық конденсатор
Потенциалдар айырмасы Сфералық конденсатордың электр сыйымдылығы келесі формуламен анықталады: 3) Цилиндрлік конденсатор
61. Конденсаторларды қосу Әрбір конденсатор тек өзінің сыйымдылығымен ғана емес, сонымен бірге максимал жұмыстық кернеуімен сипатталады. Егер конденсаторға жұмыстық кернеуден артық кернеу берілетін болса, онда конденсатор астарлары арасынан ұшқын шығып, конденсатор істен шығады. Бұл құбылыс конденсатордың тесілуі деп аталады. Берілген жұмыстық кернеу кезінде қалаған сыйымдылық алу үшін конденсаторларды тізбектей, параллель немесе аралас түрде қосады. 1) Конденсаторларды параллель қосу
Конденсаторларды параллель қосқан кездегі батареяның толық электр сыйымдылығы келесі формуламен анықталады:
2) Конденсаторларды тізбектей қосу Конденсаторларды тізбектей қосқан кезде барлық конденсаторлардағы зарядтар бірдей, конденсаторлар батареясының толық зарядына тең болады:
Конденсаторларды тізбектей қосқан кездегі батареяның толық электр сыйымдылығы келесі формуламен анықталады: Конденсаторлар аралас қосылған кезде батареяның толық сыйымдылығы олардың қосылу схемасына тәуелді және параллель немесе тізбектей қосу заңдылықтарын пайдаланып анықтауға болады. 49. көлденең жане бойлық толқындар. Қума толқындар теңдеуі. Толқын ұзындығы
Бөлшектер толқынның таралу бағытындағы келесі бөлшектерге тербелмелі қозғалыс энергиясын тасымалдайды, бірақ өздері алға қарай орын ауыстырмайды. Барлық толқындардың негізгі ерекшелігі – толқындық процестезат тасымалданбайды, энергия тасымалданады. Бірдей фазада тербелетін ең жақын нүктенің ара қашықтығы толқын ұзындығы
Мұндағы: Толқын теңдеуі тербелістегі бөлшектердің
В нүктесін кез-келген жерден таңдауға болады. Сондықтан (6.23) теңдеуін жазыққума толқын теңдеуі деп атайды. Жалпы жағдайда бұл теңдеуді мына түрде жазуға болады:
Мұндағы:
Егер толқындық сан ұғымын енгізсек (
Толқын ұзындығы (орыс. Длина волны) — толқын тербелісінің толық циклінің (периодының) ұзындығы. Толқын ұзындығы -Т периодқа тең уақыт аралығында толқын таралатын арақашықтық. Формуласы:
Бұл жерде v тербеліс жиілігі T тербеліс периоды лямбыда яғни толқын ұзындығы. Карно циклы Негізінен жылу машиналары Карно циклімен жұмыс атқарады. Карно циклі 2 изотермадан және 2 адиабатадан тұрады.
1) 1 – 2 – изотермиялық ұлғаю. 2) 2 – 3 – адиабаталық ұлғаю. 3) 3 – 4 – изотермиялық сығылу. 4) 4 – 1 – адиабаталық сығылу. Карно циклімен жұмыс кез-келген жұмыс машинасы температурасы Т1 қыздырғыштан, жұмыс денесінен және температурасы Т2 салқындатқыштан тұрады Карно теоремасы: - қайтымды Карно циклінің ПӘК-і жұмыстық дененің табиғатына және осы циклді жасайтын жүйенің құрылғысына тәуелсіз, ол тек қыздырғыш - қайтымсыз машиналардың ПӘК-і қайтымды машиналардың ПӘК-не қарағанда кіші. Карно циклі үшін ПӘК-і:
ҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚҚ 1. Қисық сызықты қозғалыс. Жылдамдық. Үдеу және оның құраушылары. Көкжиекке бұрыш жасай лақтырылған дененің қозғалысы, Жердің Күндіайнала қозғалысы кисықсызықты болып табылады. Велосипед немесеавтомобиль доңғалақта
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 1489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.211.107 (0.118 с.) |
 мұндағы:
мұндағы:  -Ван-дер-Ваальс тұрақтылары.
-Ван-дер-Ваальс тұрақтылары. мұндағы
мұндағы  - дененің кез келген Oz өсіне қатысты инерция моменті,
- дененің кез келген Oz өсіне қатысты инерция моменті,  - Oz өсіне параллель дененің массалар центрі арқылы өтетін Cz| өсіне қатысты инерция моменті, М – дененің массасы, ал d – Oz және Cz| өстері арасындағы қашықтық. Өрнектен
- Oz өсіне параллель дененің массалар центрі арқылы өтетін Cz| өсіне қатысты инерция моменті, М – дененің массасы, ал d – Oz және Cz| өстері арасындағы қашықтық. Өрнектен 
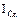 екенін көреміз. Демек, дененің ең кіші инерция моменті массалар центрі арқылы өтетін өске қатысты болады.
екенін көреміз. Демек, дененің ең кіші инерция моменті массалар центрі арқылы өтетін өске қатысты болады.



 - дегеніміз жылдамдықтары модулі
- дегеніміз жылдамдықтары модулі  интервалы арасында жататын газ молекулаларының үлесі болып табылады.
интервалы арасында жататын газ молекулаларының үлесі болып табылады. мұндағы: Т1<Т2.
мұндағы: Т1<Т2. .
. .
.
 болатыны көрінеді.
болатыны көрінеді. .
. Газ молекуласының еркін жолының орташа ұзындығы абсолют температураға тура пропорционал және газдың қысымына кері пропорционал.
Газ молекуласының еркін жолының орташа ұзындығы абсолют температураға тура пропорционал және газдың қысымына кері пропорционал. түзету көбейткішін ендірейік:
түзету көбейткішін ендірейік: =
=  2un0 (10)
2un0 (10)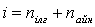
 і – молекуланың еркіндік дәрежесінің саны.
і – молекуланың еркіндік дәрежесінің саны.

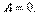

 ,
, - тұрақты көлемдегі мольдік жылу сыйымдылығы.
- тұрақты көлемдегі мольдік жылу сыйымдылығы.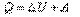
 ,
, - тұрақты қысымдағы мольдік жылу сыйымдылығы.
- тұрақты қысымдағы мольдік жылу сыйымдылығы. Майер теңдеуі. Бұдан
Майер теңдеуі. Бұдан  шығады.
шығады.
 тербеліс ығысу нүктесінен басталды
тербеліс ығысу нүктесінен басталды тербеліс тепе-теңдік күйден
тербеліс тепе-теңдік күйден (Бұл диффернциалдық теңдеудің кез келген тривиальды емес шешімі — циклді жиілігі w гармоникалық тербеліс болып табылады.)
(Бұл диффернциалдық теңдеудің кез келген тривиальды емес шешімі — циклді жиілігі w гармоникалық тербеліс болып табылады.)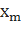 wsin(wt+
wsin(wt+  ) v=
) v=  cos(wt+
cos(wt+  r — радиус-вектор частицыp — импульс частицы.
r — радиус-вектор частицыp — импульс частицы. айн. Дененің импульс моменті
айн. Дененің импульс моменті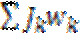 =const импульс моментінің сақталу заңы
=const импульс моментінің сақталу заңы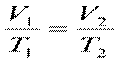


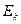 деп осы жүйедегі механикалық қозғалыстың энергиясын айтамыз. Массасы
деп осы жүйедегі механикалық қозғалыстың энергиясын айтамыз. Массасы  болатын,
болатын, 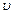 жылдамдықпен қозғалып келе жатқан дене келесі кинетикалық энергияға ие болады
жылдамдықпен қозғалып келе жатқан дене келесі кинетикалық энергияға ие болады . (2.22)
. (2.22) , мұндағы
, мұндағы  ; серіппенің серпімділік күші
; серіппенің серпімділік күші 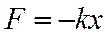 ; бүкіл әлемдік тартылыс күші
; бүкіл әлемдік тартылыс күші 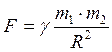 ; электр зарядтарының өзара әсерлесу күштері
; электр зарядтарының өзара әсерлесу күштері 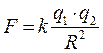 консервативті күштерге жатады.
консервативті күштерге жатады. биіктікке көтерілген дененің потенциалдық энергиясы
биіктікке көтерілген дененің потенциалдық энергиясы ; (2.23)
; (2.23) шамасына керілген серіппенің потенциалдық энергиясы
шамасына керілген серіппенің потенциалдық энергиясы ; (2.24)
; (2.24) қашықтықта орналасқан массалары m1 және m2 болатын денелердің өзара әсерлесуі кезіндегі потенциалдық энергиясы
қашықтықта орналасқан массалары m1 және m2 болатын денелердің өзара әсерлесуі кезіндегі потенциалдық энергиясы ; (2.25)
; (2.25)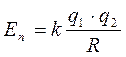 .
. айналмалықозғалыстың негізгі теңдеуі
айналмалықозғалыстың негізгі теңдеуі Клапейрон теңдеуі Бойль-Мариотт заңын, Гей-Люссак заңын және Авогадро заңын біріктіретін идеал газ күйінің теңдеуі болып табылады.
Клапейрон теңдеуі Бойль-Мариотт заңын, Гей-Люссак заңын және Авогадро заңын біріктіретін идеал газ күйінің теңдеуі болып табылады.

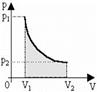
 және
және  нүктелік зарядтардың өзара әсерлесу күшінің модулі олардың шамаларының көбейтіндісіне тура, ал ара қашықтығының квадратына кері пропорционал:
нүктелік зарядтардың өзара әсерлесу күшінің модулі олардың шамаларының көбейтіндісіне тура, ал ара қашықтығының квадратына кері пропорционал: , (11.1)
, (11.1) -өлшем жүйесіне байланысты болатын пропорционалдық коэфффициент. Зарядтар арсындағы бұл күш осы зарядтар орналасқан түзу сызықтың бойымен бағытталған, яғни орталық күш болып табылады. Аттас зарядтар үшін (
-өлшем жүйесіне байланысты болатын пропорционалдық коэфффициент. Зарядтар арсындағы бұл күш осы зарядтар орналасқан түзу сызықтың бойымен бағытталған, яғни орталық күш болып табылады. Аттас зарядтар үшін (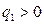 және
және 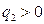 немесе
немесе  және
және  )
)  , ал зарядтар әр аттас болса,
, ал зарядтар әр аттас болса,  болады. Векторлық түрде Кулон заңы былай жазылады:
болады. Векторлық түрде Кулон заңы былай жазылады: , (11.2)
, (11.2) - бірінші зарядқа екінші зарядтың әсер етуші күші,
- бірінші зарядқа екінші зарядтың әсер етуші күші,  - бірінші зарядтан екінші зарядқа бағытталған радиус-вектор,
- бірінші зарядтан екінші зарядқа бағытталған радиус-вектор, 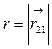 . Бұл теңдеу аттас зарядтардың бірін-бірі тебетіндігін, әр аттас зарядтардың бірін-бірі тартатындығын көрсетеді. Егер де әсерлесуші зарядтар вакуумда емес, қандай да бір ортада орналасқан болса, онда Кулон заңы былай жазылады:
. Бұл теңдеу аттас зарядтардың бірін-бірі тебетіндігін, әр аттас зарядтардың бірін-бірі тартатындығын көрсетеді. Егер де әсерлесуші зарядтар вакуумда емес, қандай да бір ортада орналасқан болса, онда Кулон заңы былай жазылады: , (11.3)
, (11.3)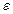 -өлшем бірлігі жоқ, ортаның электрлік қасиетін көрсетуші диэлектрлік өтімділік деп аталатын физикалық шама. Вакуум үшін
-өлшем бірлігі жоқ, ортаның электрлік қасиетін көрсетуші диэлектрлік өтімділік деп аталатын физикалық шама. Вакуум үшін  болады. Жоғарыдағы (11.1) және (11.3) теңдеулерінен
болады. Жоғарыдағы (11.1) және (11.3) теңдеулерінен  , (11.4)
, (11.4)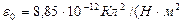 ) немесе Ф/м – электр тұрақтысы деп аталады. Осы (11.4) және (11.3) - теңдеулерге сүйене отырып, Кулон заңын төмендегідей жазуға болады:
) немесе Ф/м – электр тұрақтысы деп аталады. Осы (11.4) және (11.3) - теңдеулерге сүйене отырып, Кулон заңын төмендегідей жазуға болады: . (11.5)
. (11.5) екендігін айта кеткен жөн. Фарад (Ф) – электр сыйымдылығының өлшем бірлігі.
екендігін айта кеткен жөн. Фарад (Ф) – электр сыйымдылығының өлшем бірлігі. 1) тұрақты конденсатор 2) конденсаторлар магазині
1) тұрақты конденсатор 2) конденсаторлар магазині  Конденсатордың сыйымдылығы конденсатордың пішініне және астарлар арасындағы диэлектрик қабатының электрлік қасиетіне тәуелді.
Конденсатордың сыйымдылығы конденсатордың пішініне және астарлар арасындағы диэлектрик қабатының электрлік қасиетіне тәуелді.
 . Осы өрнектен потенциалдардың өзгерісін анықтасақ
. Осы өрнектен потенциалдардың өзгерісін анықтасақ  .
. потенциалдар айырмасы
потенциалдар айырмасы 
 екенін ескерсек, жазық конденсатордың электр сыйымдылығы келесі формуламен анықталады:
екенін ескерсек, жазық конденсатордың электр сыйымдылығы келесі формуламен анықталады:  .
.
 . Осы өрнектен потенциалдар өзгерісін анықтасақ
. Осы өрнектен потенциалдар өзгерісін анықтасақ 

 немесе
немесе 
 .
.
 .
.
 Конденсаторлар батареясындағы толық заряд
Конденсаторлар батареясындағы толық заряд 
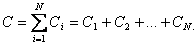
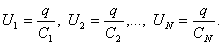


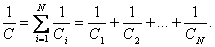
 6.7 – сурет. Көлденең толқын
6.7 – сурет. Көлденең толқын деп аталады. Бұл шама толқынның тербеліс Т периоды мен жылдамдығының көбейтіндісіне тең:
деп аталады. Бұл шама толқынның тербеліс Т периоды мен жылдамдығының көбейтіндісіне тең: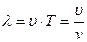 . (6.21)
. (6.21) – толқынның таралу жылдамдығы;
– толқынның таралу жылдамдығы;  – тербеліс жиілігі.
– тербеліс жиілігі. ығысуының
ығысуының  координаталар мен
координаталар мен  уақытқа тәуелділігін сипаттайды:
уақытқа тәуелділігін сипаттайды: . (6.22)
. (6.22)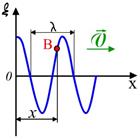 6.8 – сурет. Қума толқын
6.8 – сурет. Қума толқын жазықтықтағы нүктелер тербелісі
жазықтықтағы нүктелер тербелісі 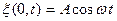 болсын. Онда толқын көзінен х қашықтықтағы В нүктесіндегі (6.8 – сурет) орта бөлшектері де осы заң бойынша, бірақ
болсын. Онда толқын көзінен х қашықтықтағы В нүктесіндегі (6.8 – сурет) орта бөлшектері де осы заң бойынша, бірақ  (мұндағы
(мұндағы  (6.23)
(6.23) . (6.24)
. (6.24) – толқын амплитудасы;
– толқын амплитудасы;  – толқынның фазасы;
– толқынның фазасы;  –циклдік жиілік;
–циклдік жиілік;  – тербелістің бастапқы фазасы. Бұл теңдеуге жылдамдық (
– тербелістің бастапқы фазасы. Бұл теңдеуге жылдамдық ( ) және циклдік жиілік (
) және циклдік жиілік ( ) өрнектерін қойсақ келесі формуланы табамыз:
) өрнектерін қойсақ келесі формуланы табамыз: (6.25)
(6.25) ), онда жазық қума толқын теңдеуін келесі түрде жазуға болады:
), онда жазық қума толқын теңдеуін келесі түрде жазуға болады: . (6.26)
. (6.26)

 пен салқындатқыштың
пен салқындатқыштың  температуралары арқылы анықталады;
температуралары арқылы анықталады;



