
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила построения кода Рида-Маллера
Коды Рида-Маллера являются линейными двоичными блочными кодами. При определенном построении они могут быть систематическими. В общем случае коды Рида-Маллера не являются циклическими. Коды Рида-Маллера задаются следующими параметрами для любых значений - длина кодового слова - длина информационной части - длина проверочной части - минимальное кодовое расстояние Коды Рида-Маллера существуют в широкой области значений скоростей передачи и минимальных расстояний. Важным достоинством кодов Рида-Маллера является то, что они могут быть декодированы сравнительно простыми методами порогового декодирования. Код Рида-Маллера определяется при помощи порождающей матрицы, состоящей из базисных векторов. Правило построения следующее: - пусть - пусть Покомпонентное произведение любых двух векторов
Пример. Для m = 4 и соответственно n = 24 = 16 запишем базисные векторы кода Рида-Маллера:
Сформированная из базисных векторов порождающая матрица может быть использована для кодирования. Чтобы получить из данной матрицы проверочную, необходимо провести ее преобразование к систематическому виду. Это обеспечивается путем сложения по модулю 2 первой строки со всеми остальными строками матрицы. Такая операция не изменяет характеристик кода. Получив проверочную и порождающую матрицы, можно проводить с кодом все операции, описанные в п. 1.3.1. Следует отметить, что при декодировании методом порогового декодирования строить проверочную матрицу нет необходимости.
Основные понятия о свойствах многочленов и полях Галуа
Операции над коэффициентами полиномов циклических кодов производятся в алгебраической системе, которая носит название поля Галуа. Полем Галуа называется конечное коммутативное поле. Конечное поле - это конечное множество из q элементов, в котором определены правила для выполнения арифметических операций. Поле Галуа из
Поля Галуа обладают следующими свойствами: - в поле определены две операции: сложение и умножение; - результатом сложения или умножения двух элементов поля является элемент этого же поля; - поле всегда содержит мультипликативную единицу 1 и аддитивную единицу 0, т.е. - для любого элемента - выполняются обычные правила ассоциативности Для каждого допустимого значения Если Если Правила умножения и сложения таких многочленов получаются из обычного умножения и сложения многочленов и последующего приведения результата по модулю некоторого специального многочлена Все конечные поля обладают тем свойством, что существует, по крайней мере, один элемент, называемый примитивным элементом, обладающий тем свойством, что любой другой элемент поля является некоторой степенью этого элемента. Неприводимый над полем Пусть неприводимый многочлен
Пусть
Запись поля Галуа осуществляется в виде набора из Построение поля проводится в следующем порядке: - записываются степени примитивного элемента от 0 до (m -1); запись производится в виде
- записывается элемент
- записываются многочлены, соответствующие остальным степеням Таким образом, поле Галуа GF(2m) запишется в виде
Умножение элементов поля Галуа сводится к сложению степеней умножаемых элементов и приведению результата в диапазон Пример. Многочлен
В соответствии с (1.21) выражение Также для построения поля Галуа важны следующие свойства: - неприводимый, т.е. неразложимый на множители над некоторым конечным полем многочлен всегда может быть разложен на множители над некоторым расширением этого поля, т.е. многочлен всегда имеет корни в некотором расширении; - если - если - корни многочлена Пример. Многочлен Элемент a является примитивным элементом поля GF (23), поэтому
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 820; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.186.241 (0.016 с.) |
 и
и  , называемого порядком кода, меньшего, чем
, называемого порядком кода, меньшего, чем  ;
;
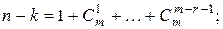
 .
. - вектор, все компоненты которого равны 1;
- вектор, все компоненты которого равны 1; - строки матрицы, столбцами которой являются все двоичные наборы длины
- строки матрицы, столбцами которой являются все двоичные наборы длины 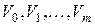 и все покомпонентные произведения
и все покомпонентные произведения  и
и  задается следующим образом:
задается следующим образом: .
.

 элементов обозначается
элементов обозначается  .
. и
и  для любого элемента
для любого элемента  , принадлежащего полю;
, принадлежащего полю; ), такой, что
), такой, что  и
и  (в случае
(в случае  обратный элемент совпадает с самим элементом);
обратный элемент совпадает с самим элементом);
 , коммутативности
, коммутативности 
 и дистрибутивности
и дистрибутивности  .
. , то элементами поля являются все многочлены степени
, то элементами поля являются все многочлены степени  или менее, коэффициенты которого лежат в простом поле
или менее, коэффициенты которого лежат в простом поле  .
. степени
степени 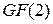 многочлен
многочлен  . При этом коэффициенты неприводимого многочлена являются элементами поля
. При этом коэффициенты неприводимого многочлена являются элементами поля  .
.
 - примитивный элемент поля
- примитивный элемент поля  .
. многочленов степени, не превышающей
многочленов степени, не превышающей  . Первый элемент записи всегда равен нулю (нулевой элемент поля) и обычно в записи не приводится. Остальные
. Первый элемент записи всегда равен нулю (нулевой элемент поля) и обычно в записи не приводится. Остальные  многочленов представляют собой степени от 0 до
многочленов представляют собой степени от 0 до  примитивного элемента поля. Здесь и далее принимается, что старшие степени многочленов записываются слева, младшие справа.
примитивного элемента поля. Здесь и далее принимается, что старшие степени многочленов записываются слева, младшие справа.
 , который определяется по правилу
, который определяется по правилу ;
; до
до 
 определяются посредством: а) умножения предыдущего многочлена, т.е. многочлена, соответствующего
определяются посредством: а) умножения предыдущего многочлена, т.е. многочлена, соответствующего 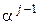 , на
, на 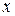 ; б) замены
; б) замены 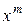 на многочлен
на многочлен 
 …
…  . Операция сложения элементов поля Галуа
. Операция сложения элементов поля Галуа  выполняется над двоичными числами по модулю 2. Степень
выполняется над двоичными числами по модулю 2. Степень  является неприводимым примитивным многочленом третей степени. Следовательно, при помощи этого многочлена может быть построено поле
является неприводимым примитивным многочленом третей степени. Следовательно, при помощи этого многочлена может быть построено поле  . Согласно формулам (1.20), поле будет иметь вид
. Согласно формулам (1.20), поле будет иметь вид .
.
 можно вычислить следующим образом: a2 + a5 = a3 = (011); a3a = a4 = (110); 1 + a3 = a = (010); aa = a2 = (100); a4 + a2 = a = (010). Таким образом, искомое выражение будет равно ¦(a) = a = (010).
можно вычислить следующим образом: a2 + a5 = a3 = (011); a3a = a4 = (110); 1 + a3 = a = (010); aa = a2 = (100); a4 + a2 = a = (010). Таким образом, искомое выражение будет равно ¦(a) = a = (010). неприводимый многочлен с коэффициентами из поля
неприводимый многочлен с коэффициентами из поля  - его корень, то
- его корень, то 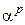 ,
,  ,
,  также будут его корнями. Все остальные корни
также будут его корнями. Все остальные корни  совпадают с ненулевыми элементами
совпадают с ненулевыми элементами  .
.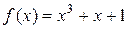 неприводим над полем
неприводим над полем  .
.


