
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие правила построения блочных кодов
В теории и технике помехоустойчивого кодирования первостепенное значение отводится решению двух задач: - построение кода, создание алгоритма кодирования и его реализация; - создание алгоритма декодирования и его реализация. Построение алгоритма кодирования сводится к разработке методов наилучшего с точки зрения задаваемых критериев разбиения кодового множества при заданных значениях n и k. Создание алгоритмов декодирования сводится к разработке методов сопоставления принятого слова с кодовым множеством с целью достижения максимальной помехоустойчивости. В случае линейных блоковых кодов построение кода сводится к получению выражений проверок на четность на позициях символов в кодовом слове. Здесь под проверкой на четность понимается сумма по модулю 2. В дальнейшем знаком суммы «+» обозначим операцию суммирования по модулю 2. Выражения для проверок могут быть представлены в следующем виде: - уравнений в символьном виде (например, - проверочной матрицы; - порождающей матрицы; - порождающего многочлена; - проверочного многочлена. Наиболее распространены и удобны выражения для проверок в виде порождающих и проверочных матриц, порождающих и проверочных многочленов. Проверочной матрицей называется матрица Проверочную матрицу и минимальное кодовое расстояние связывает свойство: если линейная комбинация (сумма) любых Пример. Пусть проверочная матрица
Тогда в формуле (1.6) первый, второй и четвертый символы являются проверочными, остальные - информационными. Кодовое слово будет определяться следующим образом:
где
Порождающей матрицей Пример. Для (7,4) (n,k)-кода, кодовое слово которого задается выражением (1.7), а проверочная матрица - выражением (1.6), порождающая матрица
Следует заметить, что матричное произведение Порождающая матрица служит для получения кодовых слов из информационных последовательностей. Действительно, если умножить двоичный вектор длины Синдромом называется вектор, определяющий наличие (иногда и положение) ошибки в принятом слове. Пусть принятое слово
Тогда при умножении принятого слова на проверочную матрицу получится вектор синдрома
Из выражения (1.10) видно, что вектор синдрома зависит только от комбинации ошибок и равен нулю в двух случаях: - когда вектор ошибки - когда вектор ошибки содержит комбинацию ошибок, совпадающую с кодовым словом. В общем случае вектор синдрома используется в табличном поиске при декодировании. В случае, когда код исправляет меньше двух ошибок, вектор синдрома может быть использован для указания местоположения ошибки. Например, для кода, определяемого матрицей H из выражения (1.6), вектор синдрома будет равен столбцу, номер которого соответствует номеру ошибочного символа в принятом слове.
Кроме матричного представления коды могут быть построены с использованием полиномиального представления кодового слова. Суть такого представления состоит в том, чтобы считать элементы кодового слова длины
Используя это обозначение, можно определить полиномиальный код как множество всех многочленов степени не большей
Кодовое слово может быть получено тремя путями: - умножением полиномов - умножением полинома - построением на основе порождающего полинома При втором способе кодовое слово получается в систематическом виде, т.е. Порождающая матрица на основе полинома g(x) имеет следующий вид (только для циклических кодов):
где Способ получения порождающей матрицы в соответствии с выражением (1.13) не является единственно возможным. Многочлен в матрице (1.13) (порождающий многочлен записан в обратном порядке) называется двойственным к порождающему. Результат кодирования по матрице Необходимо отметить, что при любом способе кодирования кодовое слово делится на порождающий многочлен без остатка. Проверочным многочленом называется многочлен степени k, полученный при делении (без остатка) полинома ( Проверочный многочлен может быть использован для получения проверочной матрицы, которая будет иметь вид:
где Следует заметить, что для циклических кодов матричное произведение Синдромным многочленом называется многочлен
Поскольку все передаваемые кодовые слова делятся без остатка на порождающий полином Коэффициенты многочленов, используемых для построения кодов, являются элементами конечного поля. Поэтому умножение, разложение на множители и другие операции над многочленами также производятся над конечными полями. Многочлены принято описывать не в виде (1.11), а в восьмеричной или двоичной форме, т.е. записывая только коэффициенты. Значение степени Пример. Многочлену
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.186.241 (0.019 с.) |
 );
);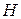 размером
размером  из
из  строк и
строк и  столбцов. В строках матрицы
столбцов. В строках матрицы  (
( ) будет проверочным тогда, когда в
) будет проверочным тогда, когда в  -м столбце матрицы
-м столбце матрицы  столбцов матрицы
столбцов матрицы  .
. .
.
 ,
,
 - первый информационный символ, третий символ в кодовом слове;
- первый информационный символ, третий символ в кодовом слове; - второй информационный символ, пятый символ в кодовом слове;
- второй информационный символ, пятый символ в кодовом слове; - третий информационный символ, шестой символ в кодовом слове;
- третий информационный символ, шестой символ в кодовом слове; - четвертый информационный символ, седьмой символ в кодовом слове;
- четвертый информационный символ, седьмой символ в кодовом слове; - первый проверочный символ, первый символ в кодовом слове;
- первый проверочный символ, первый символ в кодовом слове; - второй проверочный символ, второй символ в кодовом слове;
- второй проверочный символ, второй символ в кодовом слове; - третий проверочный символ, четвертый символ в кодовом слове.
- третий проверочный символ, четвертый символ в кодовом слове.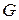 называется матрица, состоящая из
называется матрица, состоящая из 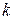 строк и
строк и  -й символ будет проверочным, когда в
-й символ будет проверочным, когда в  -м столбце содержится более одной единицы, и информационным, когда в нем содержится одна единица.
-м столбце содержится более одной единицы, и информационным, когда в нем содержится одна единица. .
.
 при этом будет равно нулю, что является показателем правильности построения этих матриц.
при этом будет равно нулю, что является показателем правильности построения этих матриц.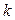 на порождающую матрицу
на порождающую матрицу  - кодовое слово, то произведение
- кодовое слово, то произведение 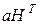 будет равно нулю.
будет равно нулю. является суммой переданного слова
является суммой переданного слова  и комбинации ошибок
и комбинации ошибок  :
: .
.
 :
: .
.
 , т.е. кодовое слово будет представляться многочленом:
, т.е. кодовое слово будет представляться многочленом: .
.
 , который называется порождающим многочленом кода. Степень полинома
, который называется порождающим многочленом кода. Степень полинома  . Информационные символы представляются при этом также многочленом степени
. Информационные символы представляются при этом также многочленом степени  , который имеет вид:
, который имеет вид: .
.
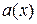 и
и 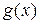 ;
;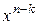 ; делением полученного произведения на полином
; делением полученного произведения на полином  до
до  ) определяют информационные символы. Остальные коэффициенты многочлена кодового слова (при степенях
) определяют информационные символы. Остальные коэффициенты многочлена кодового слова (при степенях  …0) - проверочные.
…0) - проверочные. ,
,
 - коэффициенты порождающего многочлена.
- коэффициенты порождающего многочлена. ) на g(x). Отсутствие остатка является признаком, того, что код, порождаемый многочленом g(x), является циклическим. Проверочный многочлен h(x) можно получить таким способом только для циклического кода.
) на g(x). Отсутствие остатка является признаком, того, что код, порождаемый многочленом g(x), является циклическим. Проверочный многочлен h(x) можно получить таким способом только для циклического кода. ,
,
 - коэффициенты проверочного многочлена.
- коэффициенты проверочного многочлена.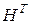 также равно нулю, хотя порождающая и проверочные матрицы получены иным способом, т.е. на основе порождающего и проверочного многочленов. Таким образом, полученная в виде (1.14) проверочная матрица может быть использована для получения синдрома в виде (1.10).
также равно нулю, хотя порождающая и проверочные матрицы получены иным способом, т.е. на основе порождающего и проверочного многочленов. Таким образом, полученная в виде (1.14) проверочная матрица может быть использована для получения синдрома в виде (1.10).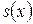 степени
степени 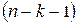 , являющийся остатком от деления принятой последовательности
, являющийся остатком от деления принятой последовательности  на порождающий многочлен, т.е.
на порождающий многочлен, т.е.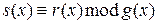 .
.
 очевидно не зависит от переданного слова, а зависит лишь от комбинации ошибок, как и в случае синдрома в (1.10).
очевидно не зависит от переданного слова, а зависит лишь от комбинации ошибок, как и в случае синдрома в (1.10).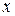 , при которой находится коэффициент в многочлене, определяет номер разряда, в котором коэффициент записывается в двоичной записи. Для сокращения записи двоичная форма представления многочлена переводится в восьмеричную запись.
, при которой находится коэффициент в многочлене, определяет номер разряда, в котором коэффициент записывается в двоичной записи. Для сокращения записи двоичная форма представления многочлена переводится в восьмеричную запись. соответствует двоичное число 1011 и восьмеричное - 13.
соответствует двоичное число 1011 и восьмеричное - 13.


