
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики помехоустойчивых кодовСтр 1 из 17Следующая ⇒
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет прикладной математики и телекоммуникаций
Кафедра радиоэлектронных средств
Е. В. МЕДВЕДЕВА А. В. ЧАСТИКОВ В. Н. ШАКИН ПОМЕХОУСТОЙЧИВЫЕ КОДЫ В РАДИОТЕХНИКЕ И СВЯЗИ
Утверждено пленумом Совета УМО по образованию в области телекоммуникации в качестве учебного пособия
Киров 2004 Печатается по решению редакционно-издательского совета Вятского государственного университета
УДК 621.391
М 42
Рецензенты: заместитель технического директора ОАО “Волга Телеком” А. Б. Герасимчук; заведующий кафедрой «Радиоэлектронные средства» доктор технических наук, профессор Е. П. Петров
Медведева Е. В. Помехоустойчивые коды в радиотехнике и связи: Учебное пособие / Е. В. Медведева, А. В. Частиков, В.Н. Шакин. - Киров: Изд-во ВятГУ, 2004. - 68с.
В пособии рассматриваются основы теории кодирования. Основное внимание уделяется помехоустойчивым кодам, позволяющим исправлять и обнаруживать ошибки, частотно-компактным кодам, предназначенным для сосредоточения энергии сигнала в возможно более узкой полосе частот и кодам, применяемым в широкополосных системах передачи информации. Приводятся описания визуальной инструментальной системы «Ecclabs» для построения помехоустойчивых кодов, проведения кодирования и декодирования и визуальной инструментальной системы «Code» для построения частотно-компактных кодов и расчета их характеристик. Пособие содержит примеры построения кодов, контрольные вопросы и методические задания к лабораторным работам по дисциплинам «Теория информации и кодирования» и может быть полезно для студентов специальностей: 201800 «Защищенные системы связи», 200900 «Сети связи и системы коммутации», 201500 «Бытовая радиоэлектронная аппаратура».
Редактор Е. Г. Козвонина
Подписано в печать Бумага офсетная Зак.№ 394 Печать копир Aficio 1022 Усл.печ.л. 4,25 Тир. 52 Бесплатно
Текст напечатан с оригинала-макета, предоставленного авторами 610000, г. Киров, ул. Московская, 36. Оформление обложки, изготовление – ПРИП ВятГУ. ã Е. В. Медведева, 2004 ã А. В. Частиков, 2004 ã В. Н. Шакин, 2004
ã Вятский государственный университет, 2004
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ Современный уровень развития цифровых систем передачи (ЦСП) предъявляет высокие требования к достоверности принимаемой информации, повышение которой за счет совершенствования каналов связи, увеличения излучаемой мощности и снижения собственного шума приемника зачастую оказывается экономически невыгодным. Более эффективным путем обеспечения требуемой степени достоверности при передаче информации является использование помехоустойчивых кодов [1-15], которые позволяют обнаруживать и исправлять ошибки в группах принятых символов. Системы передачи информации, в которых в настоящее время не применяется эффективное помехоустойчивое кодирование, считаются неперспективными. Поэтому при проектировании ЦСП, в том числе и систем проводной и беспроводной связи, на первый план выступает задача внедрения современных методов помехоустойчивого кодирования информации. Особый класс помехоустойчивых кодов образуют частотно-компактные коды или коды для линий связи [16-24]. Они предназначены для сосредоточения энергии сигнала в возможно более узкой полосе частот. Кроме того, линейный код должен осуществлять контроль ошибок на физическом уровне и не должен приводить к их размножению. Столь общая постановка задачи понимается в различных системах по-разному. В проводных линиях связи и линейных трактах, содержащих полосно-ограничивающие фильтры с крутыми фронтами, необходимо основную энергию сигнала «отодвинуть» от крайних частот к центру полосы пропускания с целью уменьшения межсимвольных искажений. В сетях радиосвязи с жесткими ограничениями по электромагнитной совместимости радиосредств кодирование должно обеспечить значительное (десятки децибел) уменьшение уровня внеполосных излучений.
В настоящее время большую часть цифровых СПИ составляют широкополосные системы. Они применяются практически во всех областях – от персональных систем связи до беспроводных локальных компьютерных сетей – и постепенно вытесняют традиционные средства передачи информации. Основными преимуществами широкополосных СПИ являются [25-32]: · высокая помехозащищенность; · электромагнитная совместимость с другими радиоэлектронными средствами; · сложность перехвата сообщений; · обеспечение кодовой синхронизации большого числа абонентов при работе в общей полосе частот; · возможность совмещения приема информации и измерения параметров движения объекта. Указанные преимущества еще более подчеркиваются и становятся очевидными при использовании шумоподобных сигналов (ШПС) с большими базами. Основой для формирования ШПС служат псевдослучайные кодовые последовательности (ПСП), используемые для модуляции сигнала несущей частоты. Учебное пособие предназначено для изучения и усвоения принципов помехоустойчивого кодирования и состоит из двух частей. Первая часть посвящена помехоустойчивым кодам. В ней описаны основные характеристики помехоустойчивых кодов, изложены правила построения кодов, обнаруживающих и исправляющих ошибки, рассмотрены правила построения поля Галуа, правила кодирования и декодирования кодов: Хэмминга, БЧХ, Рида-Соломона, Рида-Маллера, Голея, Ивадаре, Вайнера-Эша. Приведено описание визуальной инструментальной системы для построения помехоустойчивых кодов Ecclabs (разработка кафедры РЭС), позволяющей выполнять и контролировать все этапы построения, кодирования и декодирования кодов, а также правила построения кодов в этой среде. Во второй части изложены правила построения и расчет параметров кодов для линий связи. Рассмотрены особенности работы в инструментальной системе Code, предназначенной для построения и исследования частотно-компактных кодов. В третьей части рассмотрены требования предъявляемые к ПСП, основные характеристики хорошо известных, а также разработанных в последние годы ПСП. Большее внимание уделено свойствам и законам построения М-последовательностей. Каждая часть пособия завершается заданиями по исследованию кодов для лабораторных работ. Пособие предназначено для студентов специальностей 200900 «Сети связи и системы коммутации», 201800 «Защищенные системы связи» 201500 «Бытовая радиоэлектронная аппаратура» по дисциплинам “Системы документальной электросвязи” и “Теория информации и кодирования”.
ГЛАВА 1. ПОМЕХОУСТОЙЧИВЫЕ КОДЫ
Пример
Число единиц в сумме (вес суммы) равно кодовому расстоянию Кодовое расстояние, как правило, между различными кодовыми комбинациями может быть разным. Помехозащищенность кода характеризуется минимальным кодовым расстоянием Распределение рабочих кодовых комбинаций по кодовым расстояниям характеризует потенциальную помехозащищенность кода. Рассмотрим эту характеристику кода на примере. Пусть код содержит следующую совокупность кодовых комбинаций (кодовых векторов): Таблица 1.1
На основании табл.1.2 получим распределение рабочих кодовых комбинаций по кодовым расстояниям (табл.1.1). Таблица1.2
Из анализа табл.1.2 ясно, что, например, кодовый вектор Для рассматриваемого кода минимальное кодовое расстояние между рабочими векторами Потенциальная помехозащищенность кода характеризуется коэффициентом ложных переходов одной кодовой комбинации в другую под влиянием помех кратности Коэффициент ложных переходов определяет вероятность ложного перехода одной кодовой комбинации в другую под влиянием помех кратности
где Для симметричных кодов число
Общее число кодовых векторов
Для рассматриваемого примера найдем коэффициент ложных переходов при при при Таким образом, при однократной ошибке вероятность приема ложного сообщения Очевидно, чем больше Энергетическим выигрышем кода (ЭВК) называют величину
где Быструю ориентировочную оценку энергетической эффективности для оперативного сравнения кодов осуществляют по величине Корреляционные свойства кодов оценивают апериодической функцией автокорреляции (АКФ) и несколькими видами функции взаимной корреляции (ВКФ): апериодической, периодической, смешанно-периодической. Для кодового слова X, состоящего из символов ВКФ вычисляют для совокупности двух или трех кодовых слов
периодическая ВКФ между тремя словами
смешанно-периодическая ВКФ между словами
Коды, обнаруживающие ошибки Двоичный безызбыточный код Вся совокупность передаваемых сообщений может быть представлена в виде совокупности различных чисел. В этом случае имеет место числовой код. Максимальное количество возможных кодовых комбинаций в числовом коде Из всех числовых кодов наибольшее распространение получили двоичные коды. Причиной тому является простая арифметика двоичных чисел и возможность использования простых, дешевых и надежных в эксплуатации двухпозиционных элементов. Максимальное число возможных кодовых комбинаций в двоичном коде В безызбыточном двоичном коде все кодовые комбинации рабочие. Следовательно, Таким образом, безызбыточный двоичный код является непомехозащищенным кодом. Единственная защита такого кода от ошибок - фиксация нарушения количества элементов в кодовой комбинации. Поэтому, как правило, используется равномерный двоичный безызбыточный код.
Код с простым повторением
Число разрядов кода увеличивается в два раза по сравнению с безызбыточным кодом. Содержимое защитных разрядов повторяет содержимое информационных (рабочих) разрядов. Ошибки обнаруживаются путем сравнения содержимого информационных и проверочных разрядов. Число разрядов кода Пример. Рабочие комбинации кода с простым повторением (табл.1.4). Таблица 1.4
Код позволяет обнаружить все ошибки нечетной кратности и значительную часть ошибок четной кратности.
Код на одно сочетание
Числовой
Таким образом, двоичный безызбыточный код есть код на все сочетания, так как его мощность Данный код позволяет обнаружить все помехи нечетной кратности, а также все ошибки четной кратности, которые приводят к нарушению
Коды, исправляющие ошибки Основные понятия о свойствах многочленов и полях Галуа
Операции над коэффициентами полиномов циклических кодов производятся в алгебраической системе, которая носит название поля Галуа. Полем Галуа называется конечное коммутативное поле. Конечное поле - это конечное множество из q элементов, в котором определены правила для выполнения арифметических операций. Поле Галуа из Поля Галуа обладают следующими свойствами: - в поле определены две операции: сложение и умножение; - результатом сложения или умножения двух элементов поля является элемент этого же поля; - поле всегда содержит мультипликативную единицу 1 и аддитивную единицу 0, т.е. - для любого элемента - выполняются обычные правила ассоциативности Для каждого допустимого значения Если Если Правила умножения и сложения таких многочленов получаются из обычного умножения и сложения многочленов и последующего приведения результата по модулю некоторого специального многочлена Все конечные поля обладают тем свойством, что существует, по крайней мере, один элемент, называемый примитивным элементом, обладающий тем свойством, что любой другой элемент поля является некоторой степенью этого элемента. Неприводимый над полем Пусть неприводимый многочлен
Пусть Запись поля Галуа осуществляется в виде набора из Построение поля проводится в следующем порядке: - записываются степени примитивного элемента от 0 до (m -1); запись производится в виде
- записывается элемент
- записываются многочлены, соответствующие остальным степеням Таким образом, поле Галуа GF(2m) запишется в виде
Умножение элементов поля Галуа сводится к сложению степеней умножаемых элементов и приведению результата в диапазон Пример. Многочлен
В соответствии с (1.21) выражение Также для построения поля Галуа важны следующие свойства: - неприводимый, т.е. неразложимый на множители над некоторым конечным полем многочлен всегда может быть разложен на множители над некоторым расширением этого поля, т.е. многочлен всегда имеет корни в некотором расширении; - если - если - корни многочлена Пример. Многочлен Элемент a является примитивным элементом поля GF (23), поэтому
Способ 1 Кодовая комбинация циклического кода равна:
Другие кодовые комбинации циклического кода могут быть получены путем циклического сдвига данной кодовой комбинации. Процесс умножения двух полиномов реализуется схемой, показанной на рис.1.6.
Рис.1.6
Для двоичных кодов существенны только те цепи умножения, в которых Способ 2 Кодовую комбинацию для получения разделимого кода получают по алгоритму:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.61.246 (0.103 с.) |

 .
. из всех возможных кодовых расстояний для данного кода.
из всех возможных кодовых расстояний для данного кода. ,
,  ,
,  ,
,  . Найдем кодовые расстояния между всеми кодовыми векторами и поместим их в табл.1.1.
. Найдем кодовые расстояния между всеми кодовыми векторами и поместим их в табл.1.1.

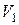


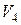



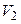


 и от двух других - на
и от двух других - на  , а вектор
, а вектор 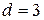 . Введем обозначение
. Введем обозначение  - число рабочих кодовых векторов, отстоящих от данного вектора на
- число рабочих кодовых векторов, отстоящих от данного вектора на 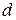 . Коды, для которых число
. Коды, для которых число  . Это означает, что даже единичная ошибка может привести к ложному (необнаруживаемому) переходу одного кодового вектора в другой. Следовательно, имеется вероятность приема ложного сообщения при искажении качественного признака одного из
. Это означает, что даже единичная ошибка может привести к ложному (необнаруживаемому) переходу одного кодового вектора в другой. Следовательно, имеется вероятность приема ложного сообщения при искажении качественного признака одного из  элементов кодовой комбинации из-за наличия помех.
элементов кодовой комбинации из-за наличия помех. ,
,
 - общее число кодовых векторов, отстоящих от данного вектора на кодовое расстояние
- общее число кодовых векторов, отстоящих от данного вектора на кодовое расстояние  определяется согласно (1.3). Для несимметричных кодов коэффициент ложных переходов
определяется согласно (1.3). Для несимметричных кодов коэффициент ложных переходов 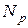 рабочих кодовых векторов, т.е.
рабочих кодовых векторов, т.е. .
.
 .
.
 ;
; ;
; .
. , при двух- и трехкратной ошибке вероятность ложного приема
, при двух- и трехкратной ошибке вероятность ложного приема  .
. обнаруживаются все ошибки кратности
обнаруживаются все ошибки кратности  . При
. При  могут быть исправлены все ошибки кратности
могут быть исправлены все ошибки кратности  , а при
, а при  (при
(при  ) обнаруживаются все ошибки кратности
) обнаруживаются все ошибки кратности  ,
, - минимально допустимое отношение сигнал-шум на входе демодулятора при некодированной передаче
- минимально допустимое отношение сигнал-шум на входе демодулятора при некодированной передаче 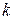 бит за время
бит за время  для получения заданного значения вероятности сбоя бита
для получения заданного значения вероятности сбоя бита  ;
;  - отношение сигнал-шум при передаче информации помехоустойчивым кодом
- отношение сигнал-шум при передаче информации помехоустойчивым кодом  .
. , апериодическую АКФ определяют как
, апериодическую АКФ определяют как  .
.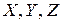 (слова
(слова  состоят из символов
состоят из символов  ,
,  ). Апериодическая ВКФ между словами X и
). Апериодическая ВКФ между словами X и 
 ;
; и
и 
 ;
;
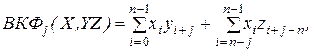
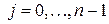 .
. .
. .
. для любого
для любого  , где
, где 

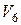

 различных кодовых комбинаций. Число
различных кодовых комбинаций. Число 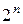 может быть представлено как сумма сочетаний из
может быть представлено как сумма сочетаний из  ,…,
,…, 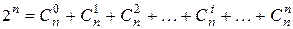 .
. . Мощность кода на одно сочетание
. Мощность кода на одно сочетание 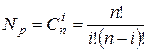 . Код образуется из двоичного безызбыточного кода путем отбора кодовых комбинаций, имеющих одинаковое число единиц. Так, для
. Код образуется из двоичного безызбыточного кода путем отбора кодовых комбинаций, имеющих одинаковое число единиц. Так, для  составляет лишь три кодовых вектора: 011,101 и 110.
составляет лишь три кодовых вектора: 011,101 и 110. .
. элементов обозначается
элементов обозначается  .
. и
и  для любого элемента
для любого элемента  , принадлежащего полю;
, принадлежащего полю; ), такой, что
), такой, что  и
и  (в случае
(в случае  обратный элемент совпадает с самим элементом);
обратный элемент совпадает с самим элементом);
 , коммутативности
, коммутативности 
 и дистрибутивности
и дистрибутивности  .
. , то элементами поля являются все многочлены степени
, то элементами поля являются все многочлены степени  или менее, коэффициенты которого лежат в простом поле
или менее, коэффициенты которого лежат в простом поле  .
. степени
степени  . Этот многочлен обладает тем свойством, что его нельзя разложить на множители, используя только многочлены с коэффициентами из поля
. Этот многочлен обладает тем свойством, что его нельзя разложить на множители, используя только многочлены с коэффициентами из поля 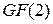 многочлен
многочлен  . При этом коэффициенты неприводимого многочлена являются элементами поля
. При этом коэффициенты неприводимого многочлена являются элементами поля  .
.
 - примитивный элемент поля
- примитивный элемент поля  .
. многочленов степени, не превышающей
многочленов степени, не превышающей  . Первый элемент записи всегда равен нулю (нулевой элемент поля) и обычно в записи не приводится. Остальные
. Первый элемент записи всегда равен нулю (нулевой элемент поля) и обычно в записи не приводится. Остальные  многочленов представляют собой степени от 0 до
многочленов представляют собой степени от 0 до  примитивного элемента поля. Здесь и далее принимается, что старшие степени многочленов записываются слева, младшие справа.
примитивного элемента поля. Здесь и далее принимается, что старшие степени многочленов записываются слева, младшие справа.
 , который определяется по правилу
, который определяется по правилу ;
; до
до 
 определяются посредством: а) умножения предыдущего многочлена, т.е. многочлена, соответствующего
определяются посредством: а) умножения предыдущего многочлена, т.е. многочлена, соответствующего 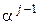 , на
, на 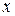 ; б) замены
; б) замены 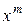 на многочлен
на многочлен 
 …
…  . Операция сложения элементов поля Галуа
. Операция сложения элементов поля Галуа  выполняется над двоичными числами по модулю 2. Степень
выполняется над двоичными числами по модулю 2. Степень  является неприводимым примитивным многочленом третей степени. Следовательно, при помощи этого многочлена может быть построено поле
является неприводимым примитивным многочленом третей степени. Следовательно, при помощи этого многочлена может быть построено поле  . Согласно формулам (1.20), поле будет иметь вид
. Согласно формулам (1.20), поле будет иметь вид .
.
 можно вычислить следующим образом: a2 + a5 = a3 = (011); a3a = a4 = (110); 1 + a3 = a = (010); aa = a2 = (100); a4 + a2 = a = (010). Таким образом, искомое выражение будет равно ¦(a) = a = (010).
можно вычислить следующим образом: a2 + a5 = a3 = (011); a3a = a4 = (110); 1 + a3 = a = (010); aa = a2 = (100); a4 + a2 = a = (010). Таким образом, искомое выражение будет равно ¦(a) = a = (010). неприводимый многочлен с коэффициентами из поля
неприводимый многочлен с коэффициентами из поля  - его корень, то
- его корень, то 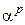 ,
,  ,
,  также будут его корнями. Все остальные корни
также будут его корнями. Все остальные корни  совпадают с ненулевыми элементами
совпадают с ненулевыми элементами  .
.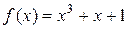 неприводим над полем
неприводим над полем  .
. =
=  =
= 
 .
.
 .
.


