
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вихідна задача двоїста задача ⇐ ПредыдущаяСтр 3 из 3
max=46X1+12X2+10X3+8X4+0(X5+X6+X7) min f =3000У1+5000У2+8000У3 3X1+4X2+4X3+5X4+X5 =4000 3У1+2У2+10У3-У4 =46 2X1+3X3+4X4+X6 =5000 4У1+12У3 -У5 =12 10X1+12X2+10X3+8X4+X7=8000 4У1+3У2+10У3-У6 =10 Xj³0 Yi³0 У вихідній задачі 7 змінних і 3 обмеження, причому додаткові змінні є базисними. Тому цю задачу відразу можна розв´язувати симплекс-методом. У двоїстій задачі 7 змінних і 4 обмеження, причому для розв´язування симплекс-методом треба вводити штучний базис, а це ще плюс 4 змінні. Тому вихідну задачу розв´язувати простіше. Запишемо її дані в симплекс-таблицю 10 і виконаємо розв´язування за алгоритмом симплексного методу. У результаті після однієї ітерації перерахування таблиці одержали в оцінному рядку всі ∆j≥0. Виходить, отриманий опорний план вихідної задачі X1=800; X2=X3=X4=0; X5=600; X6=3400; X7=0, оптимальний. Цей план випуску продукції 2. Для того, щоб знайти оптимальний план двоїстої задачі, визначимо взаємозв'язок змінних двоїстих задач і економічний зміст їх додаткових змінних. Для вихідної задачі i- а додаткова змінна
залишок i-го ресурсу
Таблиця 10 – Симплекс-таблиця для задачі розподілу ресурсів
i-а змінна двоїстої задачі означає ціну за одиницю цього ресурсу. Для двоїстої задачі j-а додаткова змінна,
різниця між сумарною вартістю витрат усіх ресурсів ym+jна одиницю j-го виду продукції та вартістю за одиницю цієї продукції. Тому ym+j(j=1,…,n)можна трактувати як характеристику рентабельності випуску j-го виду продукції. Якщо ym+j>0, тоді випуск j-го виду продукції не рентабельний (витрати більші за ціну), якщо ym+j=0, тоді випуск j-го виду продукції рентабельний. У зв´язку з вищевикладеним, основним змінним однієї задачі відповідають додаткові змінні іншої, тобто:
 Xn+i Yi Xn+i Yi  , ,
Причому для оптимальних планів цих задач випливає, що
З огляду на те, що всі змінні від´ємні, з (25) і (26) одержимо для оптимальних планів:
З (27) випливає: для оптимальних планів двоїстих задач: 1) якщо i-й ресурс цілком використовується, (X0n+i=0), тоді його ціна Y0i>0, якщо ні, (X0n+i>0), тоді його ціна y0i=0, (j=1,…, m); 2) якщо витрати на випуск одиниці j-го виду продукції більші за її ціну, Y0m+j>0, то ця продукція не випускається, X0j=0, якщо Y0m+j=0, тоді випуск j-го виду продукції рентабельний і X0j>0, (j=1,…, n). З огляду на вищесказане і відповідність змінних, знайдемо оптимальний план двоїстої задачі за даними симплекс-таблиці з оптимальним планом. Одержимо З симплекс-таблиці з оптимальним планом випливає, що min f = max Z = =36800 грош.од.. З огляду на економічний зміст змінних двоїстих задач проведемо економічний аналіз результатів. Рентабельний тільки випуск продукції першого виду (y04=0) у кількості X01=800од. Випуск інших видів продукції не рентабельний, при випуску один. продукції цих видів збитки складуть, відповідно, 43,2(У05), 36(У06), 28,8(У07) грош. одиниць. Тому X02=X03=X04=0. При такому плані випуску максимальна вартість випущеної продукції складе 36800 грош.од.. При цьому верстатні ресурси цілком витратяться, їхній залишок X07=0, вони дефіцитні, їхня ціна за один. складе В03=4,6 грош.од.. Трудові та матеріальні ресурси витрачаються не цілком, вони не дефіцитні. Тому їхня ціна за одиницю. У01=У02=0, залишки, відповідно, X05=600 і X06=3400 од. З огляду на вищевикладене, для збільшення сумарної вартості випущеної продукції необхідно збільшувати запаси дефіцитного ресурсу–верстатного. З [2;3;5] випливає, що:
Тому збільшення запасу верстатного ресурсу b3 на один. призведе до збільшення максимальної сумарної вартості випущеної продукції на В03 = 4,6 грош. од.. 3) досліджуємо допустимі межі зміни дефіцитного ресурсу, усередині яких змінні, що входять в оптимальний базис, не змінюються, тобто не змінюється асортимент продукції, що випускається, а змінюється тільки її обсяг залежно від збільшення чи зменшення ресурсу на ∆ b. Якщо дефіцитним є i-й ресурс, то, з огляду на лінійність матричних перетворень, можна показати [2;3;5], що новий оптимальний план при зміні i-го ресурсу на ∆ bi буде:
причому:
З (28) і (29) знайдемо ∆ b3, m=4
Тоді b3 + ∆b3буде змінюватися 8000-8000≤b3≤8000+2000 0≤b3≤10000 Таким чином, якщо ринок не насичений продукцією першого виду і є конкуренти, підприємству доцільно зменшити запаси трудових і матеріальних ресурсів на 600 і 3400 од.,відповідно, і за рахунок цих засобів закупити 2000 од. верстатних ресурсів. Це призведе до збільшення випуску продукції першого виду до X01 = 800+0,1·2000 = 1000 од. і вартості випущеної продукції до 46·1000 = 46000 грош. од., тобто на 4,6·2000 = 9200 грош. од.. Якщо на ринку немає конкурентів з реалізації продукції першого виду, тобто підприємство − монополіст, то збільшення вартості продукції можна досягти іншим шляхом – за рахунок збільшення її ціни. Досліджуємо допустимі межі її зміни ∆C. При цьому будемо використовувати оптимальне розв´язання двоїстої задачі В0, що знаходиться в оцінному рядку останньої таблиці. Формули, аналогічні (28), (29) мають вигляд:
причому
де У нашій таблиці це третій рядок. Тоді: ∆С1≥0∆С1≥0 43,2+1,2∆С1≥0 ∆С1≥-36 36+∆С1≥0 => ∆С1≥-36 => ∆С1≥0 28,8+0,8∆С1≥0 ∆С1≥-36 4,6+0,1∆С1≥0 ∆С1≥-46
Тоді 46≤C1<∞. Одержали, що теоретично ціну на продукцію першого виду можна збільшувати необмежено. 4) проаналізуємо доцільність розширення асортименту за рахунок випуску продукції П-5. Для цього порахуємо для отриманих оптимальних цін на ресурси їхні сумарні витрати на одиницю П-5. Одержимо 5·У01+6·У02+9·У03=5·0 + 6·0 + 9·4,6 = 41,4 грош. од. оскільки витрати менші за заплановану ціну один. продукції (41,4 < 50), то випуск продукції П-5 рентабельний і прибуток від випуску одиниці П-5 складе 8,6 грош. од.
Завдання 3 Розв´язання транспортної задачі Є три постачальники і чотири споживачі однорідного продукту. Потужності постачальників і попити споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник-споживач» зведені до таблиці 11 постачань. Задача полягає у наступному: знайти обсяги перевезень для кожної пари «постачальник - споживач» так, щоб: 1) потужності всіх постачальників були реалізовані; 2) попити всіх споживачів були задоволені; 3) сумарні витрати на перевезення були мінімальні. Таблиця 11 – Потужності постачальників і попити споживачів, витрати на перевезення одиниці вантажу
Розв´язок Поставлено збалансовану транспортну задачу, оскільки сумарний попит дорівнює сумарній потужності постачальників ® 280. Для отримання начального опорного плану перевезень скористаємось методом мінімального елемента. Для покращення будемо використовувати таблицю 12, у правому верхньому кутку якої стоїть тариф відповідного перевезення, а у лівому нижньому кутку – плановий обсяг перевезення.
Знаходимо в таблиці клітинки з найменшим тарифом. Таких клітин дві- (1;1) і (2;1) із тарифом, що дорівнює 1. Порівнюємо максимально можливі постачання для цих клітинок: для клітинки (1;1) x11=min{60,20}=20, для клітинки (2;1) x21=min{120,20}=20. Оскільки їх значення збігаються, то максимально можливе постачання записуємо в будь-яку з них. Наприклад, записуємо постачання, що дорівнює 20 од. у клітинку (2;1). У результаті попит першого споживача задоволений і перший стовпець таблиці постачань випадає з наступного розгляду, а виробничу потужність для другого рядка зменшуємо на 20 од. Аналогічним способом продовжуємо заповнювати невикреслені Таблиця 12 – Отримання начального опорного плану перевезень
клітинки таблиці. У останній клітинці попит і пропозиція повинні збігтися, оскільки розглядається збалансована задача. Слід зазначити, що в таблиці повинна бути заповнена n+m-1 клітинка перевезень (де n – число постачальників, m – число споживачів). Наприклад, для розглянутої задачі повинно бути заповнено 3+4-1=6 клітин. Остаточно одержуємо початковий опорний план перевезень. Тепер скористаємося методом потенціалів, усі розрахунки виконаємо у таблиці 13. Для цього кожному стовпцю припишемо потенціал vj, а кожному рядку – потенціал ui. Для кожної заповненої клітини складемо лінійне рівняння за правилом ui+vj=cij, де cij - тариф відповідного перевезення. Потім розв’яжемо систему 6-ти рівнянь. Оскільки в рівняннях буде 7 невідомих (3 потенціали u і 4 потенціали v), то довільний потенціал можна дорівняти до нуля. Тепер для кожної незаповненої клітинки необхідно знайти оцінку Dij= ui+vj-cij. Якщо всі оцінки будуть негативними або нульовими, то початковий опорний план є оптимальним.
Таблиця 13– Розрахунки методом потенціалів
D11=-1+3-1=1; D13=-1+7-5=1; D14=-1+4-3=0; D22=-2+3-6=-5; D23=-2+7-5=0; D31=0+3-6= -3. Оцінки D11 і D13 позитивні, отже, отримане початкове опорне розв’язання не оптимальне. З оцінок вибираємо найбільшу – D11, отже, у клітинку (1;1) будемо заносити ненульове перевезення. Заносимо в клітинку (1;1) знак «+» і будуємо ланцюг потенціалів, що може проходити тільки по заповнених клітинках, із чергуванням знаків «+» і «-» і повертається у вихідну незаповнену клітину, таблиця 14.
Cеред клітинок, позначених мінусом, вибираємо ту, що містить найменше перевезення. Це клітинка (3;4) з К=Х34 =10. У подальших обчисленнях ця клітинка буде вважатися незаповненою, тому що далі вміст вибраної клітинки,10, додаємо до вмісту клітинок, що позначені «+», і віднімаємо з клітинок, що позначені «-».У таблиці 15 повинна виявитися, як і раніше, n+m-1 заповнена клітинка. Перевіряємо отриманий опорний план на оптимальність. Таблиця 14 – Перехід до іньшого опорного плану з використанням ланцюга потенціалів
Таблиця 15 – Отриманий опорний план
D13=1; D14=-1; D22= -4; D23=1; D31= -4; D34= -1. Тому що є дві клітини (1;3) і (2;3) з позитивними оцінками, то отриманий опорний план, таблиця 15, не оптимальний. Знайдемо новий опорний план з використанням ланцюга потенціалів, таблиця 15. Оскільки дві позитивні оцінки набувають однакових позитивних значень, D13=D23=1, то можна занести ненульове перевезення або в клітинку (1;3), або в клітинку (2;3). Якщо у ланцюг будє включено клітинку (1;3),таблиця 15, то це перевезення буде дорівнювати 40 од.. Таким чіном одержано новий опорний план, таблиця 16.
Таблиця 16 – Оптимальний опорний план
Перевіряємо отриманий опорний план на оптимальність.
D14= -1; D22= -4; D23= 0; D31= -4; D33= -1; D34= -1.
Оскільки серед оцінок немає позитивних, можна сказати, що отриманий опорний план є оптимальним, але не єдиним (D23= 0). У підсумку підприємствам можна запропонувати наступний план перевезень:
Завдання 4 Розв´язання задачі про призначення У конструкторському бюро потрібно розробити проект машини, що складається із чотирьох вузлів. До їх розробки можна залучити чотирьох конструкторів. Відомий час, що витрачається кожним конструктором на розробку будь-якого вузла. Потрібно визначити, хто і який вузол машини повинен проектувати, щоб сумарний час проектування всієї машини був мінімальним. Розв´язок Нехай необхідно розв’язати задачу про призначення, якщо задана матриця витрат часу на розробку будь-якого вузла кожним конструктором:
1. Приведемо матрицю до такого вигляду, щоб у кожному стовпці й кожному рядку знаходився хоча б один нуль. Для цього знайдемо в кожному рядку матриці мінімальний елемент і віднімемо його від усіх елементів відповідного рядка. Аналогічні перетворення виконаємо також з елементами стовпців.
2. Якщо після першого кроку можливий вибір чотирьох незалежних нулів, тоді можна стверджувати, що задача розв’язана. Незалежні нулі для зручності будемо позначати (*). При розставленні позначок найкраще вибирати рядок або стовпець, що містять найменшу кількість нулів. У цьому рядку (стовпці) вибираємо нуль, позначаємо його і викреслюємо інші нулі в рядку чи стовпці, на перетині яких знаходиться вибраний (або незалежний) нуль. Позначки ставимо доти, доки в матриці існують вільні (непозначені або невикреслені) нулі.
У розглянутому прикладі не вдалося відразу ж одержати оптимальне розв’язання, отже, переходимо до виконання третього кроку. 3. Проведемо мінімальне число горизонтальних і вертикальних ліній, що перетинають, принаймні, один раз усі нулі. Для задач невеликої розмірності візуально легко нанести шукані лінії, для більш складних зручно використати наступний алгоритм: 1. Позначаємо всі рядки, що не містять незалежних нулів. 2. Позначаємо всі стовпці, що містять нуль хоча б в одному позначеному рядку. 3. Позначаємо всі рядки, що містять незалежні нулі в позначених стовпцях. Кроки 2 і 3 виконуємо доти, доки можливо ставити позначки. Далі викреслюємо непозначені рядки і позначені стовпці.
Якщо виявилося, що кількість ліній дорівнює n,тоді необхідно повернутися на попередній крок (позначки нулів) і знову вибрати незалежні нулі. Такий варіант можливий, якщо при проставлянні позначок 2 або більше нулів у рядку мали «однакове право» бути незалежними. 4. Серед елементів, через які не пройшла жодна з ліній, обираємо найменший. Віднімаємо це число від усіх елементів, через які не пройшла жодна лінія, і додаємо його до всіх елементів, через які проведені дві лінії.
5.
Повертаємося до кроку вибору незалежних нулів. У розглянутому прикладі одержуємо відразу два оптимальних розв’язання: 1-ше завдання ® 1-й ресурс; 2-ге завдання ® 2-й ресурс (або 4-й ресурс); 3-тє завдання ® 3-й ресурс; 4-те завдання ® 4-й ресурс (або 2-й ресурс). У результаті такого призначення система виконає всі завдання за 17 умовних одиниць часу. Зауваження. У тому випадку, якщо необхідно розв’язати задачу отримання максимального значення функції мети, можна скористатися наступною формулою переходу, що слушна для будь-якої задачі лінійного і нелінійного програмування: min (L) = - max (-L)(тобто елементи матриці С помножити на (-1)). Завдання 5 Розв’язати задачу цілочислового програмування
Розв’язання Зведемо ЗЛП до канонічного вигляду, помноживши перше рівняння на –1.
Оскільки в рівняннях обмежень відсутні базисні змінні, то введемо штучні базисні змінні
Таблиця 17– Симплекс-таблиця М-задачі
Оскільки Складемо правильне відсічення
Оскільки Одержимо
Додамо це обмеження новим рядком до симплекс-таблиці 18. Оскільки Dj Таблиця 18– Симплекс-таблиця
Зауваження. Якщо розв’язувати З Ц П. на максимум функції мети f, тоді штучні базисні змінні додаються до функції мети з коефіцієнтами – М. ПИТАННЯ ДО ЗАЛІКУ
1. Задачі, що приводять до поняття математичного програмування. 2. Загальна постановка задач математичного програмування. 3. Загальна задача лінійного програмування (З З Л П). 4. Властивості розв’язання 3 Л П. 5. Графічний метод розв’язання 3 Л П. 6. Симплексний метод розв’язання 3 Л П. 7. Побудова опорних планів 3 Л П. 8. Умови оптимальності опорного плану 3 Л П. 9. Алгоритм симплексного методу. 10. Метод штучного базису. 11. Двоїсті задачі лінійного програмування. Економічна інтерпретація цих задач та їхніх розв’язків. 12. Види двоїстих задач. Теореми подвійності. 13. Постановка транспортної задачі (Т 3). 14. Математична модель Т 3. 15. Умова збалансованості Т 3. 16. Зв'язок Т 3 із задачею лінійного програмування (3 Л П). 17. Визначення розв’язання (плану) Т 3. 18. Умова можливості розв'язання Т 3. 19. Визначення опорного плану Т 3. 20. Виродженість і невиродженість опорного плану. 21. Зв'язок виродженості й невиродженості опорного плану Т 3 із заповнюванням таблиці Т 3. 22. Визначення циклу в таблиці Т 3. 23. Зв'язок опорного плану Т 3 з циклічністю. 24. Метод північно-західного кута для визначення початкового опорного плану. 25. Метод мінімального елемента. 26. Метод Фогеля. 27. Суть методу потенціалів. 28. Вимоги до опорності плану при застосуванні методу потенціалів. 29. Постановка задачі про призначення. 30. Математична модель задачі про призначення. 31. Задача про призначення як різновид Т 3 зі своєю специфікою. 32. Розв’зання (план) задачі про призначення. 33. Теорема 1 про мінімізацію функціонала. 34. Теорема 2 (Фробеніуса). 35. Застосування теорем 1 і 2 для занулення матриці С. 36. Визначення «незалежного» нуля в матриці С. 37. Зв'язок “незалежних” нулів з оптимальністю плану задачі про призначення. 38. Суть угорського методу при розв’язанні задачі про призначення. 39. Якщо при розв’язанні задачі про призначення угорським методом не отриманий оптимальний план, яким буде подальше розв’язання задачі? 40. Постановка задачі цілочислового програмування (З Ц П). 41. Математична модель З Ц П. 42. Зв'язок розв’язання З Ц П з розв’язанням З Л П. 43. Способи розв’язання З Ц П. 44. Розв’язання З Ц П методами «відсічення», поняття «правильного» відсічення. 45. Геометрична ілюстрація методу «відсічення». 46. Метод Гоморі, побудова «правильного» відсічення. 47. Алгоритм методу Гоморі.
СПИСОК ЛІТЕРАТУРИ
Основна література 1. Акулич И.Л. Математическое программирование в примерах и задачах / И. Л. Акулич. – Москва: Высшая школа, 1986. – 336 с. 2. Ашманов С.А. Линейное программирование / С.А. Ашманов. – Москва: Наука, 1981. – 289 с. 3. Кузнецов Ю. Н. Математическое программирование / Ю. Н. Кузнецов, В. И. Кузубов, А. Б. Волошенко. – Москва: Высшая школа, 1980. – 331с. 4. Кузнецов А. В. Сборник задач по математическому программированию / А. В. Кузнецов, Г. И. Новикова, Н. И. Холод. – Минск: Вышейшая школа, 1985. – 403 с. 5. Карманов В. Д. Математическое программирование / В. Д. Карманов. – Москва: Высшая школа, 1980. – 257 с. Додаткова література 6. Сакович В. А. Исследование операций (детерминированные методы и модели) / В. А. Сакович. – Минск: Вышейшая школа, 1984. –296 с. 7. Черніченко В. Є. Навчальний посібник для практичних занять і контрольних робіт з дисципліни “Математичне програмування” для студентів денної та заочної форм навчання зі всіх спеціальностей економічного факультету та факультету менеджменту / В. Є. Черніченко. – Кременчук: КДПУ, 2003. –33 с. 8. Черніченко В. Є. Навчальний посібник з дисципліни “Математичне програмування” на теми “Транспортна задача”, “Задача про призначення”, “Цілочислове програмування” для студентів денної та заочної форм навчання зі всіх спеціальностей факультетів економічного та управління (частина II) / В. Є. Черніченко. – Кременчук: КДПУ, 2005. –37 с. 9. Черніченко В. Є. Методичні вказівки щодо проведення лабораторної роботи з навчальної дисципліни “Математичне програмування” з теми “Нелінійне програмування. Квадратичне програмування ” для студентів денної та заочної форм навчання з усіх спеціальностей факультетів економічного та управління/ В. Є. Черніченко. – Кременчук: КДПУ, 2006. –15 с.
Додаток А Зразок оформлення титульної сторінки семестрового практичного завдання
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ КРЕМЕНЧУЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ІМЕНІ МИХАЙЛА ОСТРОГРАДСЬКОГО
кафедра ЕКОНОМІКИ ШИФР (НОМЕР ЗАЛІКОВОЇ КНИЖКИ)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.184 (0.192 с.) |
 5У1+4У2+8У3-У7 =8
5У1+4У2+8У3-У7 =8
 =(800;0;0;0;600;3400;0) забезпечує її максимальну сумарну вартість max Z = 36800 грош. од.
=(800;0;0;0;600;3400;0) забезпечує її максимальну сумарну вартість max Z = 36800 грош. од.
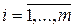 для опорного плану вихідної задачі,
для опорного плану вихідної задачі,  ,
, ,
, Ym+i Xi
Ym+i Xi  .
.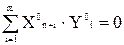 , (25)
, (25) . (26)
. (26)
 X0n+i=0 y0i>0 чи X0n+i>0 Y0i=0, (27)
X0n+i=0 y0i>0 чи X0n+i>0 Y0i=0, (27)
 Y0m+j=0 X0j>0 чи Y0m+j>0 X0j=0.
Y0m+j=0 X0j>0 чи Y0m+j>0 X0j=0. =(0;0;4,6;0;43,2;36;28,8)
=(0;0;4,6;0;43,2;36;28,8) .
. (28)
(28) (29)
(29)

 ,
, ,
, - вектор – рядок останньої симплекс-таблиці, який відповідає виду продукції, що випускається.
- вектор – рядок останньої симплекс-таблиці, який відповідає виду продукції, що випускається.







 100
100

 bj
bj


 -4
-4




 При такому розподілі перевезень потужності всіх постачальників будуть реалізовані, попит усіх споживачів задоволений, сумарні витрати складуть:
При такому розподілі перевезень потужності всіх постачальників будуть реалізовані, попит усіх споживачів задоволений, сумарні витрати складуть: грош. од.
грош. од. .
.
















 ,
,  і розв’яжемо М-задачу в симплекс-таблиці 17.
і розв’яжемо М-задачу в симплекс-таблиці 17.
 , то отриманий план З Л П:
, то отриманий план З Л П:  не цілочисловий. Застосуємо метод Гоморі і знайдемо розв’язання З Ц П.
не цілочисловий. Застосуємо метод Гоморі і знайдемо розв’язання З Ц П. .
. , то для побудови відсікання можна взяти будь-який рядок, наприклад, другий.
, то для побудови відсікання можна взяти будь-який рядок, наприклад, другий.
 , то отриманий план:
, то отриманий план:  , оптимальний, цілочисловий,
, оптимальний, цілочисловий, 



