Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угловая скорость тела равна первой производной от угла поворота по времени.
Отношение Dw к Dt называют средним угловым ускорением
Угловое ускорение тела равно первой производной от угловой скорости по времени. Перемещения S и скорости точек S = здесь R − радиус вращения.
Нормальное (центростремительное)
Полное ускорение точки:
Модули скоростей и ускорений точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения. Равнопеременное вращение тела При равнопеременном вращении твердого тела вокруг неподвижной оси: ε= const Так как После интегрирования с учетом начальных условий получим: ω=ω0+ε t
Пример 1. Груз, опускаясь согласно уравнению Решение. Скорость груза равна скорости точки М барабана
Угловое ускорение При t1=2c:
Нормальное ускорение:
Тангенциальное ускорение:
Полное ускорение:
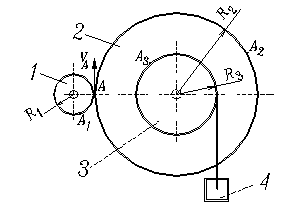
Пример 2. Вал 1 с зубчатым колесом 1 при вращении делает n=300 об./мин. Колесо 1 находится в зацеплении с зубчатым колесом 2. Радиусы делительных окружностей колес составляют R1=10 см, R2=50 см. На валу 2 смонтирован барабан 3 радиуса R3= 20 см, который вращается вместе с зубчатым колесом 2. Найти скорость перемещения груза 4, подвешенного на тросе.
Решение. 1. Угловая скорость колеса 1: ω1= p n/ 30 = 10p с−1 2. Линейные скорости точек, колес 1, 2 в точках контакта А равны в любой момент времени: vA= ω1 R1= ω2 R2 = 100 p см/с такую же скорость имеют точки А1, А2. 3. Угловая скорость колеса 2 и барабана 3: ω2= ω1 R1 /R2= 2 p с−1 4. Скорость перемещения груза 4, такую же скорость имеют точки на наружной поверхности барабана (например, т. А3): v 4=ω2 R3= 40 p см/с Пример 3. При условии предыдущей задачи определить ускорение в т. А1, А2 и груза 4 через 1,5 с. после начала вращения. Время разгона равно 2 с., движение считаем равноускоренным. При равноускоренном движении угловое ускорение колеса 1: ε=const; ω1=ω01+ε1t Т. к. при t=0; ω1=0; а при t1=2 с. ω1= 10p с−1
ε1=ω1 /t1 = 5p с−2 Угловое ускорение колеса 2: ε2=ε1 R1 /R2= p с−2 Угловые скорости колес 1, 2 при t1=1,5 с. ω1=ε1t = 7,5p с−1 ω2=ε2t =1,5 p с−1 Скорости т. А1, А2 при t1=1,5 с vA1=vA2=ω1 R1 =75 p см/с Скорости т. А3 и груза 4 при t1=1,5 с. vA3=v4= ω2 R3 = 30 p см/с Тангенциальные и нормальные ускорения т. А1, А2 при t1=1,5 с аτ A1 =аτ A2 = ε1 R1 =ε2 R2 = 50 p см/с2 аn A1 = ω12R1 =562,5 p2 см/с2 аn A2 = ω22R2 =112,5 p2 см/с2 Тангенциальные и нормальные ускорения т. А3 при t1=1,5 с. аτ A3 = ε2 R3 = 20 p см/с2 аn A3 = ω22R3 =45 p2 см/с2 Ускорение груза 4 при t1=1,5 с. а 4= аτ A3 = 20 p см/с2
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.32.230 (0.011 с.) |
 . Угловое ускорение:
. Угловое ускорение:
 можно определить из соотношений:
можно определить из соотношений: ;
; .
.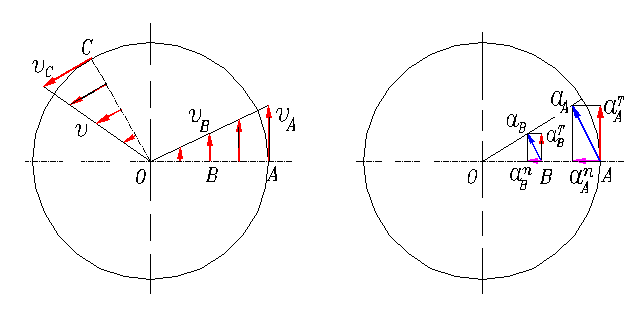
 и тангенциальное (вращательное)
и тангенциальное (вращательное)  ускорения определим из соотношений:
ускорения определим из соотношений: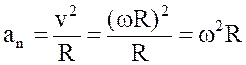 ,
, 
 ;
;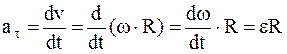 ,
, 

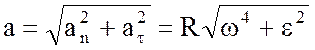 .
.
 φ=φ0 +ω0t+ε t2/2, здесь ω0 и φ0 − угловая скорость и угол поворота в начальный момент времени при t=0.
φ=φ0 +ω0t+ε t2/2, здесь ω0 и φ0 − угловая скорость и угол поворота в начальный момент времени при t=0. (м), приводит посредством троса в движение барабан радиуса R = 0,2м (рис.11.10). Определить скорость и ускорение точки М барабана при t1= 2с.
(м), приводит посредством троса в движение барабан радиуса R = 0,2м (рис.11.10). Определить скорость и ускорение точки М барабана при t1= 2с.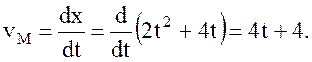 Угловая скорость барабана:
Угловая скорость барабана: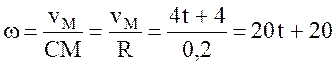 .
.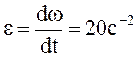 .
. ,
, 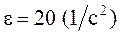 ;
;
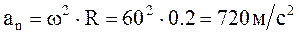 ,
,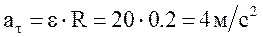 ,
, .
.