
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поступательное движение твердого тела полностью определяется движением одной его точки.Стр 1 из 4Следующая ⇒
Вектор скорости Скоростью точки М, определяющей как быстро и в каком направлении она движется в данный момент времени t, называют предел
Вектор скорости равен первой производной от радиуса-вектора точки по времени. Так как предельным положением секущей ММ1 является касательная к траектории точки, то и вектор ее скорости Вектор ускорения
характеризующий изменение скорости в данный момент времени t, называют ускорением точки. Вектор ускорения равен первой производной от вектора скорости точки по времени или второй производной от радиуса-вектора точки по времени. Ускорение, Координатный способ задания движения В прямолинейной системе координат Oxyz вектор
1. Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:
2. Проекции ускорения на оси координат равны первым производным от проекций скоростей точки или вторым производным от соответствующих координат точки по времени:
Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам
а направления
Задание движения в естественных осях Предельное положение прямой, проходящей через точки М и М1 траектории L точки М, когда М1 стремится к М, определяет касательную к этой кривой в точке М. Обозначим Соприкасающаяся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М кривой и любую точку М1 на ней, когда М1 стремится к М. Нормаль Прямоугольную систему взаимно ортогональных осей, направленных по
Радиусом кривизны «r» кривой L в точке М называют величину обратную ее кривизне в этой точке
Так, например, дуга окружности длиной s, опирающаяся на центральный угол где R – радиус окружности, то радиус кривизны для окружности Ускорение точки можно разложить на тангенциальное
Нормальное ускорение
Абсолютная величина
Задача. По заданным уравнениям движения точки x = 2t (см), определить ее траекторию, положение, скорость, ускорение, касательное и нормальное ускорения, радиус кривизны траектории в заданное время t1 = 2c. Решение.
Построим траекторию по точкам: 2.Величина скорости точки 3. Величина ускорения точки 4.Касательное ускорение
5.Нормальное ускорение при t1 = 2c: 6.Радиус кривизны траектории
Кинематика твердого тела Твердые тела можно рассматривать как совокупность точек, расстояния между которыми в процессе их перемещения остаются неизменными. Угол между пересекающимися прямыми, связанными с телом, сохраняется без изменения, а параллельные прямые остаются параллельными при его движении. Положение точек твердого тела полностью определено, если известно положение трех его точек, не лежащих на одной прямой.
1. Простейшие движения твердого тела К простейшим относятся поступательное и вращательное движение тела вокруг неподвижной оси. 1.1. Поступательное движение. При поступательном движении любой отрезок прямой (например, отрезок АВ), проведенный в твердом теле, остается параллельным самому себе.
Выберем подвижную систему отсчета Axyz, оси которой связаны с данным телом и передвигаются вместе с ним. Т. к. при поступательном движении оси координат остаются параллельными своему начальному направлению, координаты любой точки (например т. В) твердого тела в подвижной системе отсчета остаются постоянными, а ее движение тождественно движению т. А. Следовательно, траектории движения всех точек одинаковы. Одинаковыми по модулю и направлению будут также скорости и ускорения твердого тела при его поступательном движении. Ускорения точки. Абсолютное ускорение точки характеризует абсолютное изменение скорости на абсолютном перемещении, а переносное и относительное − изменение соответствующих скоростей при её переносном и относительном движении.
Теорема Кориолиса. Абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного аОТ, характеризующего изменение относительной скорости vОТ в относительном движении, переносного аПЕР, характеризующего изменение переносной скорости v ПЕР в переносном движении, и кориолисова а С, характеризующего изменение относительной скорости в переносном движении и переносной скорости в относительном движении
Величина аС, характеризующая изменение вектора относительной скорости v ОТ в переносном движении и вектора переносной скорости v ПЕР в относительном движении, называется поворотным или кориолисовым ускорением. Кориолисово ускорение равно удвоенному векторному произведению угловой переносной скорости на относительную скорость точки.
Если угол между векторами v ОТ и ω ПЕР обозначить через α, то по модулю: а С=2 ω ПЕР vОТ sinα Вектор а Снаправлен перпендикулярно плоскости, проходящей через векторы ω и vОТ. Направление вектора можно определить, если повернуть вектор vОТ (или его проекции на плоскость, перпендикулярную Относительное аОТ и переносное аПЕР ускорения точки вычисляются по известным формулам кинематики. Направления ускорений для кривошипно-кулисного механизма показаны на рисунке. При постоянной угловой скорости кривошипа. В частности, для рассмотренного ранее примера. vПЕР =vа sin(45°+ωt/2) vОТ =vа cos(45°+ωt/2) aПЕРτ=vа ω cos(45°+ωt/2)/2 aПЕРn= ω ПЕР2O1A aОТ=−vа ω sin(45°+ωt)/2 ас=2 ω ПЕР vОТ sinα; α=90°; O1A=2OA cos(45°−ωt/2) Для положения механизма, показанного на рис. ωt=30° О1А=0,346 м; ω ПЕР =5 с−1; vа=2 м/с; vОТ=1 м/с; aПЕРτ=5 м/с2; aПЕРn=8,66 м/с2; aОТ=− 8,66 м/с2; ас=5 м/с2 Проекция абсолютного ускорения на линию О1А (ось X):
Проекция абсолютного ускорения на линию ┴О1А (осьY): a┴О1А= ас+aПЕРτ=10 м/с2 Абсолютное ускорение аа=(aО1А2+a┴О1А2)0,5=20 м/с2 и направлено от т. А к т. О. Тот же ответ получим, если определим аа как нормальное ускорение т. А при ее вращательном движении вокруг т. О: aАn= ω 2OA. Направление ускорений при движении точки по поверхности шара, вращающегося вокруг неподвижной оси, показано на рис.
Пример. Дано: радиусы шкивов В, С, D, начальная угловая скорость ременной передачи ω0 =0, угловое ускорение шкивов 1 ε1 (1/c) при запуске.
Решение: 1. Угловые скорости и ускорения: ω1 = ε1t1; т. к. ω1 В= ω2 D; и ε1В= ε2 D ω2 =ω1 В/ D; ε2=ε1 В/ D 2. Линейные скорости т. L, М, N, и груза G vМ=vL=ω1 В; vN=vG= ω1С 3. Тангенциальные ускорения аМτ = аLτ =ε1В; аNτ =ε1С 4. Нормальные ускорения аМn =ω2 2D аLn =ω12В аNn =ω12С. 5. Полные ускорения аG = аNτ =ε1С; аМ = … Задание.. Дано: радиусы шкивов В, С, D, начальная скорость груза vG=0, а его скорость v G =2 t (м/c). Таблица. Исходные данные.
Найти угловые скорости шкивов, линейные скорости и ускорения точек на наружных поверхностях шкивов, а также скорость и ускорение груза G через 1 c.
Вектор скорости Скоростью точки М, определяющей как быстро и в каком направлении она движется в данный момент времени t, называют предел
Вектор скорости равен первой производной от радиуса-вектора точки по времени. Так как предельным положением секущей ММ1 является касательная к траектории точки, то и вектор ее скорости Вектор ускорения
характеризующий изменение скорости в данный момент времени t, называют ускорением точки. Вектор ускорения равен первой производной от вектора скорости точки по времени или второй производной от радиуса-вектора точки по времени. Ускорение, Координатный способ задания движения В прямолинейной системе координат Oxyz вектор
1. Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:
2. Проекции ускорения на оси координат равны первым производным от проекций скоростей точки или вторым производным от соответствующих координат точки по времени:
Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам
а направления
Задание движения в естественных осях Предельное положение прямой, проходящей через точки М и М1 траектории L точки М, когда М1 стремится к М, определяет касательную к этой кривой в точке М. Обозначим Соприкасающаяся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М кривой и любую точку М1 на ней, когда М1 стремится к М. Нормаль Прямоугольную систему взаимно ортогональных осей, направленных по
Радиусом кривизны «r» кривой L в точке М называют величину обратную ее кривизне в этой точке
Так, например, дуга окружности длиной s, опирающаяся на центральный угол где R – радиус окружности, то радиус кривизны для окружности Ускорение точки можно разложить на тангенциальное
Нормальное ускорение
Абсолютная величина
Задача. По заданным уравнениям движения точки x = 2t (см), определить ее траекторию, положение, скорость, ускорение, касательное и нормальное ускорения, радиус кривизны траектории в заданное время t1 = 2c. Решение.
Построим траекторию по точкам: 2.Величина скорости точки 3. Величина ускорения точки 4.Касательное ускорение
5.Нормальное ускорение при t1 = 2c: 6.Радиус кривизны траектории
Кинематика твердого тела Твердые тела можно рассматривать как совокупность точек, расстояния между которыми в процессе их перемещения остаются неизменными. Угол между пересекающимися прямыми, связанными с телом, сохраняется без изменения, а параллельные прямые остаются параллельными при его движении. Положение точек твердого тела полностью определено, если известно положение трех его точек, не лежащих на одной прямой.
1. Простейшие движения твердого тела К простейшим относятся поступательное и вращательное движение тела вокруг неподвижной оси. 1.1. Поступательное движение. При поступательном движении любой отрезок прямой (например, отрезок АВ), проведенный в твердом теле, остается параллельным самому себе.
Выберем подвижную систему отсчета Axyz, оси которой связаны с данным телом и передвигаются вместе с ним. Т. к. при поступательном движении оси координат остаются параллельными своему начальному направлению, координаты любой точки (например т. В) твердого тела в подвижной системе отсчета остаются постоянными, а ее движение тождественно движению т. А. Следовательно, траектории движения всех точек одинаковы. Одинаковыми по модулю и направлению будут также скорости и ускорения твердого тела при его поступательном движении. Поступательное движение твердого тела полностью определяется движением одной его точки. Все точки тела движутся по идентичным траекториям, а их скорости и ускорения одинаковы. Скорости и ускорения при простейших движениях точек тела при его поступательном движении 1. Равномерное прямолинейное движение (v=const) по оси Х x=x0+v t, a =0. 2. Равномерное криволинейное движение (v=const) s=s0+v t,
где s − дуговая координата; s0 − дуговая координата в начальный момент времени при t=0. 3. Равноускоренное движение (a =const) v=v0+ аτ t здесь v0 − начальная скорость при t=0. 1.2. Вращательное движение твердого тела Вращательным движением называется такое движение, при котором любые две точки, принадлежащие телу, остаются неподвижными.
Прямая, соединяющая эти точки называется осью вращения все точки этой прямой также остаются неподвижными. Остальные точки тела движутся по окружностям в параллельных плоскостях, перпендикулярных оси вращения, а их центры расположены на оси вращения. Такое движение вполне определяется углом поворота тела j относительно некоторого начального положения:
За время Dt угол j изменяется на величину Dj. Отношение Dj к Dt называют средней угловой скоростью тела за время Dt, Угловая скорость тела:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.106.241 (0.116 с.) |

 в данный момент времени t направлен по касательной к траектории в сторону движения.
в данный момент времени t направлен по касательной к траектории в сторону движения. Величину
Величину  называют средним ускорением точки за время
называют средним ускорением точки за время  . Предел отношения
. Предел отношения ,
, направлено в сторону вогнутости траектории.
направлено в сторону вогнутости траектории. может быть представлен в виде
может быть представлен в виде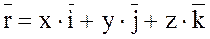 ,
, координаты точки М, определяющие закон ее движения в зависимости от времени t;
координаты точки М, определяющие закон ее движения в зависимости от времени t; - нормированный базис Oxyz.
- нормированный базис Oxyz.

 ,
, и
и  характеризуют их направляющие косинусы
характеризуют их направляющие косинусы .
. - единичный направляющий вектор касательной к L в точке М.
- единичный направляющий вектор касательной к L в точке М. к кривой в точке М, лежащую в соприкасающейся плоскости, называют главной нормалью к кривой в т.М. Нормаль
к кривой в точке М, лежащую в соприкасающейся плоскости, называют главной нормалью к кривой в т.М. Нормаль  к кривой, перпендикулярную соприкасающейся плоскости, называют бинормалью.
к кривой, перпендикулярную соприкасающейся плоскости, называют бинормалью. называют естественными осями кривой L. Направление вектора скорости принимают за положительное направление касательной
называют естественными осями кривой L. Направление вектора скорости принимают за положительное направление касательной  .
.

 Положительное направление главной нормали считают в сторону вогнутости кривой, а бинормаль направляют так, чтобы получившаяся система осей
Положительное направление главной нормали считают в сторону вогнутости кривой, а бинормаль направляют так, чтобы получившаяся система осей  являлась правой.
являлась правой. Кривизной «k» кривой L в точке М называют предел
Кривизной «k» кривой L в точке М называют предел .
. .
.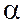 :
:  ,
,
 , направленное по касательной к траектории и характеризующее изменение величины скорости, и нормальное
, направленное по касательной к траектории и характеризующее изменение величины скорости, и нормальное  , направленное по главной нормали к центру кривизны траектории и определяющее изменение направления
, направленное по главной нормали к центру кривизны траектории и определяющее изменение направления 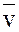 .
. Так как в естественных осях траектории скорость может быть представлена в виде
Так как в естественных осях траектории скорость может быть представлена в виде 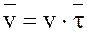 , то, дифференцируя это соотношение по времени, получим ускорение:
, то, дифференцируя это соотношение по времени, получим ускорение: , Касательное ускорение (проекция ускорения точки на касательную) равно первой производной от величины скорости от времени:
, Касательное ускорение (проекция ускорения точки на касательную) равно первой производной от величины скорости от времени: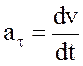
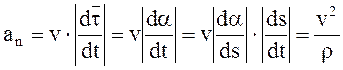
 может быть определена по формуле
может быть определена по формуле .
. (см)
(см) 1.Уравнение траектории получим, исключив из уравнений движения время:
1.Уравнение траектории получим, исключив из уравнений движения время:  - парабола с вершиной в точке (0,-2).
- парабола с вершиной в точке (0,-2).
 ;
;  см/с;
см/с;  ; при t1=2с, vx=2 см/с vy=6см/с;
; при t1=2с, vx=2 см/с vy=6см/с; 
 ;
;  ;
;  ;
;  .
. ; при t1 = 2с
; при t1 = 2с  .
. ;
; .
.
 ; при t1 = 2c
; при t1 = 2c см.
см.

 При суммировании ускорений нужно учитывать также изменения относительной скорости за счет переносного движения и переносной за счет относительного движения. Соответствующие приращения скоростей показаны на рис. а, б: d2vОТ и d1vПЕР. Оба приращения направлены в одну сторону и равны
При суммировании ускорений нужно учитывать также изменения относительной скорости за счет переносного движения и переносной за счет относительного движения. Соответствующие приращения скоростей показаны на рис. а, б: d2vОТ и d1vПЕР. Оба приращения направлены в одну сторону и равны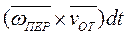


 ) на 90° в сторону переносного вращения.
) на 90° в сторону переносного вращения. aО1А= −aПЕРn +aОТ =−17,32 м/с2
aО1А= −aПЕРn +aОТ =−17,32 м/с2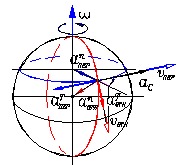
 Найти угловые скорости шкивов, линейные скорости и ускорения точек на наружных поверхностях шкивов, а также скорость и ускорение груза G через t1 c.
Найти угловые скорости шкивов, линейные скорости и ускорения точек на наружных поверхностях шкивов, а также скорость и ускорение груза G через t1 c.




 .
.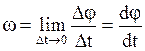 .
.


