
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к заданию 1.1Стр 1 из 4Следующая ⇒
Введение Методы линейного программирования – необходимый инструмент современного инженера, экономиста, программиста. В условиях рыночных отношений нередко приходится решать задачи планирования производства. Часто руководящему составу предприятия приходится определять, какую продукцию выпускать фирме и в каком количестве. При этом естественным требованием планирования производства является получение наибольшей выгоды, прибыли. Производство сопровождается обязательным ограничением (лимитом) имеющихся ресурсов: электроэнергии, топлива, комплектующих деталей, станочного времени, сырья и т.п. Нередко на практике встречаются задачи оптимальных перевозок товаров от предприятий-производителей к предприятиям-потребителям (транспортные задачи). Линейное программирование – раздел математического программирования, наука, которая помогает организовать производство для получения максимальной выгоды при наличии имеющихся ограничений. При этом ограничения и целевая функция описываются простейшими математическими моделями - линейными уравнениями. В процессе выполнения заданий студенты осваивают графический и аналитический способы планирования производства. Кроме того, они получают навыки работы с математическими пакетами MATLAB, Mathcad и электронными таблицами MS Excel. При проведении лабораторных работ преподаватели могут по своему усмотрению делать акцент на любой математической системе или на электронных таблицах. В данных методических указаниях достаточно подробно рассмотрен случай, когда график целевой функции параллелен графику одного из ограничений. Эта ситуация неверно описывается в известных литературных источниках, а широко распространенные программы в ряде случаев дают ошибочный ответ. Авторы выражают благодарность Садовой Е. за помощь в разработке условий задач линейного программирования. Линейное программирование
Подготовка к работе По указанной литературе и Приложению изучить основные понятия математического программирования (МП), ознакомиться с методами решения задач линейного программирования (ЛПР), математическими системами Mathcad, MATLAB и приложением MS Excel. Ответить на контрольные вопросы.
2. Контрольные вопросы 2.1. Сформулируйте в общем виде задачу математического программирования. 2.2. Чем отличаются задачи линейного программирования и задачи нелинейного программирования? 2.3. Приведите примеры целевых функций. 2.4. Какова наибольшая размерность задачи ЛПР, которую можно решить графически? 2.5. С помощью каких математических систем можно решать задачи ЛПР? 2.6. Как перейти от задачи минимизации целевой функции к задаче её максимизации? 2.7. Перечислите основные этапы решения задачи ЛПР графическим способом. 2.8. Каков порядок решения задач ЛПР с помощью электронных таблиц MS Excel? 2.9. Каковы недостатки решения задач ЛПР при помощи MS Excel? 2.10. Как построить двухмерные и трехмерные графики с помощью математической системы Mathcad? 2.11. Что такое область допустимых решений? 2.12. Сколько точек соприкосновения может иметь график ЦФ с полигоном допустимых решений при оптимальном решении задачи ЛПР? 2.13. Перечислите методы решения задач ЛПР. 2.14. Дайте характеристику задачам линейного, нелинейного, целочисленного, параметрического, дробно-линейного, стохастического и динамического программирования. 2.15. Перечислите сферы использования теории математического программирования. 2.16. Почему задачи линейного программирования порой называют оптимизационными задачами? 2.17. Опишите порядок решения задач ЛПР с помощью симплекс-метода.
Задания на выполнение лабораторной работы
3.1. Задание 1 1.1. Графически и аналитически решить задачу максимизации целевой функции Z. Исходные данные необходимо выбрать из таблицы 1 в соответствии со своим вариантом. Таблица 1
1.2. Выполнить предыдущий пункт, используя приложение MS Excel. Сравнить полученные в пунктах 1.1 и 1.2 результаты, сделать выводы.
Задание 2 2.1. Графически и аналитически решить задачу максимизации целевой функции Z согласно варианту. Исходные данные приведены в таблице 2. Таблица 2
2.2. Выполнить первый пункт задания, используя приложение MS Excel. По полученным результатам сделать выводы.
Задание 3 3.1. Графически и аналитически поочередно решить задачи максимизации трех целевых функций Z1, Z2, Z3 при одинаковых ограничениях. Исходные данные необходимо взять из таблицы 3 в соответствии с вариантом.
Таблица 3
3.2. Выполнить предыдущий пункт, используя приложение MS Excel. Сравнить полученные результаты, на основании чего сделать выводы.
Задание 4 4.1. Графически и аналитически решить задачу максимизации целевой функции Z. Найти оптимальное решение с учетом стоимости ресурсов. Исходные данные для каждого варианта приведены в таблице 4. Таблица 4
Примечание. Символами с1, с2 и с3 обозначены стоимости соответственно первого, второго и третьего ресурсов b1, b2 и b3.
4.2. Выполнить предыдущий пункт, используя приложение MS Excel. По полученным в двух пунктах результатам сделать выводы.
Задание 5 С помощью математической системы Mathcad максимизировать целевую функцию Z, приведенную в таблице 5. По результатам расчета построить трехмерный график, на котором изобразить плоскости ограничений и плоскость рассчитанной ЦФ. На графике показать точку оптимума.
Таблица 5
Задание 6 С помощью математической системы Mathcad решить транспортную задачу. Исходные данные приведены в таблице 6. Таблица 6
Задание 7 С помощью математической системы MATLAB повторно решить задачу 1 (табл.1). Сопоставить результаты с результатами, полученными в п.п. 1.1 и 1.2.
Задание 8 Составить программу для решения задачи ЛПР с помощью симплекс-метода. Произвести расчет задачи ЛПР (табл.1). Программу и результат поместить в отчет.
Методические указания
Пример графического и аналитического решения задачи ЛПР Пусть дана целевая функция (ЦФ) Z=5х1+7х2, а также ограничения: х1+4х2≤ 16, 5х1+х2≤ 23, х1≥ 0, х2≥ 0. Требуется максимизировать ЦФ. Чтобы найти решение графически, вначале следует изобразить многоугольник (полигон) допустимых решений. Для этого, используя первое ограничение, вначале запишем уравнение х1+4х2=16. Оно получено из неравенства заменой знака «≤» на знак «=». Для построения прямой линии х1+4х2=16 достаточно двух точек. Первую точку удобно взять при х1 = 0, а вторую точку при х2 = 0. Используя второе ограничение, аналогично строят прямую линию 5х1+х2=23. Нетрудно заметить, что прямые х1=0 и х2=0 (третье и четвертое ограничения) являются осями координат х1 и х2.
Отметим стрелками полуплоскости, которые удовлетворяют заданным неравенствам. Область, удовлетворяющая всем четырем неравенствам, будет областью (полигоном) допустимых решений. На рис. 1 полигон допустимых решений показан светло-серым цветом. Теперь построим график ЦФ, приравняв Z к нулю (можно взять любое число). Обозначим этот график символами Z0. Для максимизации ЦФ будем перемещать прямую линию в направлении градиента возрастания ЦФ до тех пор, пока прямая линия не достигнет границы полигона допустимых решений. Из рисунка 1 видно, что оптимум находится в точке A. Запишем приблизительные координаты этой точки: х1 = 4, х2 = 3. На основании приближенного графического решения задачи ЛПР найдём точный ответ аналитически. Для этого используем метод подстановок. Из рисунка 1 видно, что точка оптимума находится на пересечении двух прямых: х1+4х2=16, 5х1+х2=23. Для точного определения координат выразим в первом уравнении х1 через х2: х1=16-4х2. Подставим значение х1 во второе уравнение и определим неизвестные величины: 5·(16-4х2)+х2=23. 80-20х2+х2=23. 19х2=57. х2=3. х1=16-4х2=16-4·3. х1=4.
Полученные значения х1 и х2 подставляем в ЦФ: Z=5х1+7х2=5·4+7·3 Таким образом, максимальное значение ЦФ Z=41.
Рис. 1. Полигон допустимых решений
В ответ записываем значения х1 = 4, х2 = 3 и Z = 41.
Пример решения задачи ЛПР с использованием приложения MS Excel Решим предыдущую задачу с помощью приложения MS Excel. Для этого создадим таблицу, в которую запишем формулы, начальные значения и пояснения:
Примечание. Чтобы увидеть формулы в ячейках электронной таблицы, нужно последовательно активизировать пункты меню Сервис – Параметры. В появившемся меню следует выбрать вкладку Вид, и в Параметрах окна поставить флажок напротив слова формулы. Чтобы обратно переключиться в режим, показывающий значения вместо формул, необходимо этот флажок убрать. В ячейках B1 и B2 находятся исходные (начальные) значения х1 и х2 соответственно. Эти числа могут быть практически любыми. В ячейку B3 записана формула данной ЦФ (целевая функция определена в исходных данных). В ячейки D2 и D3 занесены ограничения (только левая их часть, до знака «≤»). Условия неотрицательности (х1≥ 0, х2≥ 0) в таблицу не заносятся – они будут указаны при поиске решения. Теперь в меню Сервис выбираем пункт Поиск решения… Появляется диалоговое окно, которое заполняем следующим образом:
В поле Установить целевую ячейку указываем ячейку B3, содержащую формулу ЦФ. Так как необходимо максимизировать ЦФ, то переключатель Равной следует установить в положение максимальному значению. В поле Изменяя ячейки указываем ячейки с начальными значениями х1 и х2. В поле Ограничения заносим условия неотрицательности (х1≥ 0, х2≥ 0). Также здесь указываем ячейки с ограничениями, вписывая их значение после знака «≤». Нажимаем кнопку Выполнить, после чего выбираем Сохранить найденное решение. После этого в электронной таблице в соответствующих полях появятся координаты х1 и х2 точки оптимума и значение ЦФ:
Как видим, в данном случае аналитическое решение задачи и ее решение с помощью Ms Excel дали одинаковый ответ.
Начало блока вычислений Given Опишем ограничения: x1 ≥ 0 x2 ≥ 0 x3 ≥ 0 19x1 + 20x2 – 21x3 ≤ 125 31x1 - 29x2 + 32x3 ≤ 85 -42x1 + 40x2 + 38x3 ≤ 80 Выполним операцию максимизации: P:= Maximize(Z,x1,x2,x3) Выведем на экран значения найденных переменных:
Вычислим целевую функцию: Z(P0, P1,P2) = 61.132
Итак, оптимальные значения переменных: х1 = 4,485, х2 = 4,467, x3 = 2,36. Максимальное значение ЦФ Z = 61,132. Построим трехмерный график, который показывает ограничения и оптимальное положение целевой функции. Присвоим значение ЦФ переменной R: R:= Z(P0, P1,P2) Создадим циклы для изменения переменных х1 и х2: x1:=0..P0 + 5 x2:=0..P1 + 5 Выразим переменную х3 из трех ограничений и целевой функции:
Организованы циклы tj:= 1 si:= 1
Введен вектор запасов
Введен вектор спроса
Введена целевая функция xm,n:=0 Given
В двух последних выражениях следует обратить внимание на форму знаков равенства (жирный знак равенства) x ≥ 0 x:=Minimize(Z,x)
Приложение
Математическое программирование (МП) – математическая дисциплина, которая занимается разработкой методов нахождения экстремума (максимума или минимума) функции многих переменных при наличии ограничений на эти переменные. В общем виде задачу МП можно сформулировать следующим образом: требуется максимизировать (или минимизировать) целевую функцию (ЦФ) Z = f(x1, x2,…,xn) (1) при наличии ограничений на допустимые значения переменных (аргументов) x1, x2,…,xn: gi(x1, x2,…,xn) ≤ bi где bi – некоторые действительные числа (ресурсы, лимиты); выражение в скобках означает, что индекс i изменяется от 1 до m. Величина m показывает, сколько ограничений имеется в данной задаче. Величина n определяет число переменных в задаче (например, число видов выпускаемой продукции). В прикладных задачах ограничениями на допустимые значения переменных (аргументов) могут быть: фонд рабочего времени, количество сырья, энергетические ресурсы (газ, нефть) и т.п.. Результат решения задачи МП должен оцениваться количественной мерой – критерием оптимальности. Критерием оптимальности называется количественная оценка качества решения задачи МП (качества планирования производства). На основании выбранного критерия оптимальности составляется целевая функция, которая представляет собой зависимость критерия оптимальности от оптимизируемых переменных (аргументов). Например, доход (критерий оптимальности) зависит от числа производимых заводом радиоприемников (первая переменная х1), числа производимых телефонных аппаратов (вторая переменная х2) и числа компьютеров (третья переменная х3). В качестве критериев могут выступать, например, прибыль (при решении её нужно максимизировать), затраты (их нужно минимизировать). Переход от процедуры минимизации ЦФ к её максимизации прост: для этого достаточно сменить знак целевой функции (это достигается умножением ЦФ на минус единицу). По этой причине в дальнейшем будем говорить чаще всего только о максимизации ЦФ, понимая, что переход к минимизации ЦФ несложен. Процедуру перехода от минимизации к максимизации иллюстрирует следующий рисунок.
Рис. П1. Переход от максимизации к минимизации
О математическом программировании часто говорят, как о дисциплине, занимающейся решением экстремальных задач при наличии ограничений. Эти же задачи порой называют оптимизационными, так как разработанные методы их решения позволяют получить наилучшее (оптимальное) решение среди множества допустимых решений. В зависимости от вида целевой функции Z и функций ограничений gi, математическое программирование можно рассматривать как ряд достаточно самостоятельных дисциплин (разделов математического программирования). Так, если целевая функция и функции имеющихся ограничений линейны, то такая задача является задачей линейного программирования (ЛПР). Если же целевая функция или хотя бы одна функция ограничений нелинейная, то такая задача является задачей нелинейного программирования. В задачах целочисленного программирования неизвестные (аргументы) могут принимать только целые значения. В задачах параметрического программирования целевая функция или функции ограничений зависят от параметров. В задачах дробно-линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных значений переменных, являются линейными. Если в целевой функции или в функциях ограничений содержатся случайные величины, то такая задача относится к задаче стохастического программирования. Наконец, задача, процесс решения которой является многоэтапным (многошаговым), относится к задачам динамического программирования. Наиболее детально разработаны и чаще других применяются на практике методы решения задач линейного программирования. Такие задачи встречаются в различных отраслях экономики (управление промышленными объектами, планирование производства), науки и техники (выбор наилучшей конструкции устройства), сельского хозяйства (составление рационов питания для животных), обороны (планирование боевых операций) и т.п. Термин «линейное программирование» сходен по звучанию с термином «программирование», то есть составление программ (кодирование) для ЭВМ. Однако это разные понятия. Термин линейное программирование возник в результате неточного перевода английского термина «linear programming». Правильным переводом термина «linear programming» должно быть не «линейное программирование», а «линейное планирование». Под термином «линейное программирование» следует понимать науку, которая занимается разработкой оптимальных планов организации производства. При этом все используемые в линейном программировании функции должны быть линейными. Заметим, что первые постановки задач линейного программирования были сделаны известным советским математиком Л.В.Канторовичем. С помощью теории линейного программирования можно, например, составить штатное расписание отдела технического контроля завода, выбрать вид и объем производимой фирмой продукции, спланировать работу гидроэнергетического комплекса, оптимизировать раскрой материалов или подготовить планы транспортных перевозок. Рассмотрим порядок построения области допустимых решений
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.200.211 (0.208 с.) |





















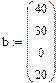







































 , (2)
, (2)



