Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №2. Исследование асимметричной системы шифрования RSA
2.1 Цель работы: изучение системы шифрования с открытым ключом RSA, получение навыков шифрования и выбора параметров шифросистемы.
2.2 Предварительная подготовка
2.2.1 Необходимо ознакомиться с основными сведениями о системах шифрования с открытыми ключами. 2.2.2. Исследовать принцип работы программы RSA.
2.3 Рабочее задание
2.3.1 Используя значения p и q, заданные таблицей построить ключевую пару (e, d) для алгоритма RSA.
Т а б л и ц а 2.1
2.3.2 Зашифровать с помощью открытого ключа напарника (n, e) сообщение, состоящее из первых букв собственной фамилии, имени и отчества и передать его адресату. 2.3.3 Получив от напарника зашифрованное сообщение, расшифровать его, используя собственный секретный ключ. 2.3.4 Используя программную реализацию алгоритма RSA, с помощью компьютера проверить правильность результатов, полученных при шифровании и расшифровании сообщений, используемых в пункте 2.3.2. 2.3.5. Вычислить цифровую подпись открытого сообщения, передаваемого в п. 2.3.2. Для этого использовать экспоненту расшифрования, определенную в пункте 2.3.1, и программу, реализующую алгоритм RSA на компьютере. 2.3.6 Проверить полученную в п.2.3.5 цифровую подпись, используя экспоненту расшифрования и программу, реализующую алгоритм RSA.
2.4 Методические указания по выполнению работы
2.4.1 Наиболее важной частью алгоритма RSA, как и других алгоритмов с открытым ключом, является процесс создания пары открытый/секретный ключи. В RSA он состоит из следующих шагов. 1. Согласно номеру компьютера выберите значения двух секретных простых чисел, p и q, p¹q. Допустим, что p=17, q=31. 2. Вычислите n=p*q=17*31=527. 3. Согласно заданной формуле, рассчитайте функцию Эйлера 4. Пользуясь методом подбора, который должен отвечать условию Существует второй способ нахождения ключевой пары (e, d). При нахождении значений e и d, удовлетворяющих условию
В общем случае это уравнение имеет вид Решение этого уравнения можно получить с помощью разложения отношения где а для всех членов, начиная с третьего, справедливо Таким образом, для решения уравнения необходимо представить отношение a/b в виде цепной дроби, определить при этом значения r0, r1…rм и м. Потом определяются значения ai, bi, а также x и y. 2.4.2 Чтобы зашифровать данные открытым ключом (n, e), необходимо: 1. Разбить исходный текст на блоки, каждый из которых может быть представлен в виде числа M(i)=0, 1,..., n-1. Допустим, наше сообщение имеет следующий вид: RSA. Представим данное сообщение в виде последовательности чисел, содержащихся в интервале 0…526. Для этого буквы R, S и A закодируем пятимерными двоичными векторами, воспользовавшись двоичной записью их порядковых номеров в алфавите: R = 18 = (10010), S = 19 (10011), A = 1 (00001). Тогда RSA = (100101001100001). Укладываясь в заданный интервал 0…526, получаем следующее представление: RSA = (100101001), (100001) = (M1 = 297, M2 = 33). 2. Необходимо зашифровать последовательность чисел по формуле Таким образом, 1.4.3 Чтобы расшифровать эти данные секретным ключом (n, d), необходимо выполнить следующие вычисления Таким образом, Возвращаясь к буквенной записи, получаем после расшифрования RSA. 1.4.4 Используя программную реализацию алгоритма RSA версии 1.1.0, с помощью компьютера проверим правильность результатов, полученных при шифровании и расшифровании сообщений. Вводим p, e и q. Производим расчет.
Рисунок 2.1 – Формирование ключей для шифрования сообщения «RSA»
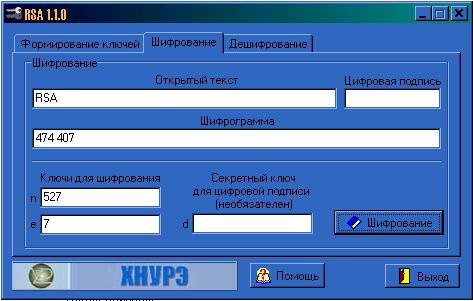
Далее переходим на следующую вкладку «Шифрование» и пишем свое сообщение в поле «Открытый текст». Нажимаем на кнопку «Шифрование». У нас появляется шифрограмма.
Рисунок 2.2 – Шифрование сообщения «RSA» без цифровой подписи.
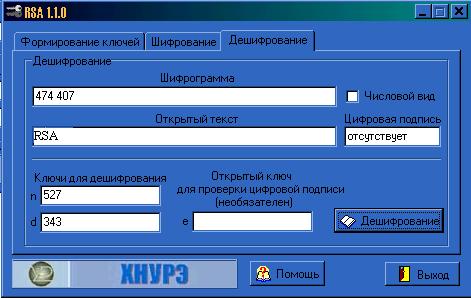
Дешифрование представляет собой обратный процесс. Переходим по вкладке «Дешифрование» и нажимаем кнопку «Дешифрование». В поле «Открытый текст» появляется расшифрованное сообщение «RSA».
Рисунок 2.3 – Дешифрование шифрограммы «474 407» без цифровой подписи.
2.4.5 Для шифрования с цифровой подписью в поле «Цифровая подпись» вводим некоторый текст, который и станет цифровой подписью - «Защита». При этом необходимо в поле «Секретный ключ» указать значение d. После шифрования, в поле «Шифрограмма» появляется зашифрованное сообщение с добавленной цифровой подписью.
Рисунок 2.4 – Шифрование сообщения «RSA» с цифровой подписью.
При дешифровании с цифровой подписью необходимо в поле «Открытый ключ» указать значение е.
Рисунок 2.5 – Дешифрование шифрограммы «474 407» с цифровой подписью.
1.5 Контрольные вопросы
1. Какие числа являются простыми, взаимно простыми? Как проверить, является ли выбранное число простым? 2. Дайте определение несимметричных шифров. 3. Как осуществляется шифрование и расшифрование сообщений в алгоритме RSA?. 4. Какие соображения следует принимать при выборе чисел p, q, n? 5. Сложностью какой математической задачи определяется стойкость системы RSA? 6. Что общего между обычной и цифровой подписями? Чем они различаются? 7. Какие задачи позволяет решать цифровая подпись?
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.165.246 (0.013 с.) |
 .
. , рассчитайте значения e, k и d. Открытый (e) и секретный (d) ключи должны быть взаимно простыми. В нашем случае e=7, k=5, d=343.
, рассчитайте значения e, k и d. Открытый (e) и секретный (d) ключи должны быть взаимно простыми. В нашем случае e=7, k=5, d=343. , значение e обычно задают таким образом, чтобы оно было взаимно простым с
, значение e обычно задают таким образом, чтобы оно было взаимно простым с  , а значение d определяют из уравнения
, а значение d определяют из уравнения (где
(где  ) и называется Диафантовым уравнением.
) и называется Диафантовым уравнением.
 в цепную дробь.
в цепную дробь.
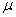 – порядок цепной дроби, т.е. индекс коэффициента дроби, у которого остаток равен нулю,
– порядок цепной дроби, т.е. индекс коэффициента дроби, у которого остаток равен нулю,

 .
. .
. .
.