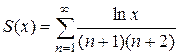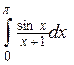Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
For (инициализация; проверка; приращение)Стр 1 из 3Следующая ⇒
Содержание
1 Лабораторная работа. Использование базовых и дополнительных структур С++ при решении задач. Характерные приемы программирования 4 2 Лабораторная работа. Использование структур языка С++ при решении задач численными методами 9 3 Лабораторная работа. Массивы и их обработка 14 4 Лабораторная работа. Методы сортировки массивов 18 5 Лабораторная работа. Обработка символьных данных 22 6 Лабораторная работа. Работа со структурами и объединениями 25 7 Лабораторная работа. Файлы и работа с ними 29 8 Лабораторная работа. Функции. Рекурсия 30 Приложение А 34 Список литературы 35
1 Лабораторная работа. Использование базовых и дополнительных структур С++ при решении задач. Характерные приемы программирования Цель: научиться практически применятьзнания, полученные в курсе Информатики, к решению задач вычислительного характера на языке высокого уровня С++; получить практические навыки работы со стандартными алгоритмами – характерными приемами программирования в С++.
Общие сведения 1.1.1 Любой сложный алгоритм можно представить, используя три основные управляющие конструкции. К базовым относят: а) следование - обозначает последовательное выполнение действий; б) ветвление - выбор одного из двух вариантов действий; в) цикл-пока - определяет повторение действий, пока не будет нарушено некоторое условие, выполнение которого проверяется в начале цикла. Кроме базовых, процедурные языки программирования высокого уровня используют три дополнительные конструкции, реализуемые через базовые: а) выбор - выбор одного варианта из нескольких в зависимости от значения некоторой величины; б) цикл-до - повторение действий до выполнения заданного условия, проверка которого осуществляется после выполнения действий в цикле; в) цикл с заданным числом повторений (счетный цикл) - повторение некоторых действий указанное количество раз. Перечисленные конструкции были положены в основу структурного программирования, а в языках программирования высокого уровня появились управляющие операторы для их реализации. Для изображения алгоритмов структурных программ могут использоваться: 1) блок-схемы; 2) псевдокоды; 3) Flow-формы; 4) диаграммы Насси-Шнейдермана.
В таблице А.1 отражается соответствие различных способов описания алгоритмов.
1.1.2 Программы, написанные с использованием только структурных операторов передачи управления, называют структурными, чтобы подчеркнуть их отличие от программ, разрабатываемых с использованием низкоуровневых способов передачи управления. Каждой управляющей конструкции, рассмотренной в п.1.1.1, можно поставить в соответствие оператор С++. Так, например, к базовым следует отнести: а) оператор присваивания переменная = выражение; б) оператор условного перехода: - в полной форме if (условие) оператор1; else оператор2; - в краткой форме if (условие) оператор; в) оператор цикла с предварительным условием (с предусловием) while (условие) или while (условие) { оператор; оператор1; оператор2; операторN; } Дополнительным конструкциям следует поставить в соответствие: а) оператор- переключатель switch (оператор выбора или варианта) Switch (выражение) { case n1: оператор1; break; case n2: оператор2; break; case nk: операторК; break; default: операторN; break; } б) троичный условный оператор (выражение1)? выражение2: выражение3; в) оператор цикла с последующим условием (с постусловием) do или do { {оператор;} оператор1; while (условие); оператор2; … операторN; } while (условие); г) оператор цикла с параметром Задание к лабораторной работе Выбрать вариант по таблице 1.1 и решить задачу, используя базовые и дополнительные структуры. К каждой задаче построить блок-схему. Организовать диалог с пользователем. Таблица 1.1 – Варианты заданий
Продолжение таблицы 1.1
Окончание таблицы 1.1
1.3 Контрольные вопросы 1.3.1 Какие алгоритмические структуры относятся к базовым? Какие к дополнительным? Приведите примеры базовых и дополнительных структур. 1.3.2 Как графически изображаются схемы алгоритмов? Какое преимущество имеют Flow-формы и диаграммы Насси-Шнейдермана? Какие достоинства и недостатки имеют блок-схемы? 1.3.3 В чем отличие между оператором и операцией? Какие виды операций существуют? Перечислите известные Вам операции присваивания в С++. 1.3.4 В заключаются особенности форматного ввода – вывода? 1.3.5 Какие операторы С++ реализуют ветвление? В чем их особенности? Приведите примеры использования.
1.3.6 Какую структуру имеет оператор выбора? С какой целью используется оператор break? 1.3.7 Какие операторы С++ реализуют циклы? В чем их особенности? Приведите примеры использования. 1.3.8 Как с помощью цикла while можно сымитировать цикл for? 1.3.9 Приведите алгоритм поиска среднего арифметического элементов последовательности а1, а2, а3 …а10. Чем будет отличаться поиск среднего геометрического элементов той же последовательности? 1.3.10Приведите алгоритм поиска максимального значения среди элементов последовательности а1, а2, а3 …а10.
2 Лабораторная работа. Использование структур языка С++ при решении задач численными методами Цель: получить практические навыки использования возможностей языка программирования для решения математических задач.
Общие сведения Одной из характерных особенностей современности является успешное применение математических методов в самых различных областях человеческой деятельности. Однако часто встречаются задачи, решение которых не удается получить в виде формулы, связывающей искомые величины с заданными, т.е. в явном виде. Для их решения стремятся получить какой-нибудь бесконечный процесс, сходящийся к искомому результату. Если такой процесс найден, то, выполняя некоторое число шагов и затем, обрывая вычисления, можно получить приближенное решение задачи. Эта процедура достаточно трудоемкая и связана с проведением вычислений по строго определенному алгоритму. Применение численных методов на базе компьютерной техники существенно расширило класс математических задач, допускающих исчерпывающий анализ. Например, часто в математических вычислениях возникает необходимость определить сумму бесконечного ряда с заданной точностью. На такие задачи налагается жесткое условие: ряд должен быть сходящимся, т.е. абсолютное значение текущего элемента ряда должно быть меньше абсолютного значения его предыдущего элемента. В подобных случаях можно пользоваться итерационными циклами, реализуемыми операторами цикла с предварительным и с последующим условиями. Иначе условие выхода из цикла никогда не будет выполнено и цикл станет бесконечным. Если определен способ вычисления текущего значения заданной последовательности по предыдущему значению, то говорят, что задана рекуррентная формула вычисления элемента последовательности. В таком способе задания есть необходимый атрибут – явно заданное начальное значение этой последовательности. При вычислении элементов заданной рекуррентно последовательности может использоваться любой из операторов цикла в зависимости от поставленной задачи.
При вычислении корней алгебраического уравнения с заданной точностью ε успешно используются методы итераций, касательных (Ньютона) и дихотомии (деления отрезка пополам). Для вычисления определенных интегралов существуют метод прямоугольников и метод Симпсона. Алгоритмы вычислений с помощью этих методов подробно рассматриваются в [1, 12].
Задание к лабораторной работе 2.2.1 Вычислить значение суммы (см. таблицу 2.1) с заданной пользователем точностью ε. Таблица 2.1 – Варианты заданий
Окончание таблицы 2.1
2.2.2 В соответствии с выбранным вариантом (см. таблицу 2.2) выполнить вычисления: Таблица 2.2 – Варианты заданий
Окончание таблицы 2.2
2.3 Контрольные вопросы 2.3.1 Какие вычислительные процессы считаются итерационными? 2.3.2 Какие формулы называются рекуррентными?
2.3.3 С какой целью в итерационных циклах используются условия? 2.3.4 Каковы преимущества численных методов интегрирования? 2.3.5 В каких случаях целесообразно применение численных методов интегрирования? 2.3.6 В чем заключается суть метода дихотомии? 2.3.7 Приведите алгоритм метода прямоугольников. 2.3.8 В чем заключается суть метода итераций? 2.3.9 Приведите алгоритм метода Симпсона. 2.3.10 Каковы особенности метода касательных?
Общие сведения Массив — это упорядоченный набор элементов одинакового типа, имеющих общее имя. Все элементы массива пронумерованы. Порядковый номер элемента в массиве называется индексом. Массивы должны быть обязательно описаны перед использованием в программе. Различают одномерные (векторы), двумерные (матрицы) и многомерные массивы, однако на практике массивы размерностью свыше трех используются крайне редко. Общий вид объявления массива: тип_элементов имя_массива [N1][N2]...[Nk]; Количество индексов [N1][N2]...[Nk] определяет размерность массива. При объявлении массива указывается общее число элементов массива. Индексация элементов массива в С++ по умолчанию начинается с нуля. Размер массива может задаваться константой или константным выражением. Нельзя задать массив переменного размера, для этой цели используется отдельный механизм - динамическое выделение памяти. В языке C++ возможна инициализация массива при его объявлении. К элементам массива применимы две операции: присваивание и выборка. Для выборки элементов массива и их обработки чаще всего используются циклы.
Задание к лабораторной работе Решить задачу, соответствующую варианту, выбранному по таблице 3.1. Построить блок-схему программы и организовать ввод данных, если это необходимо, с помощью генератора случайных чисел. Таблица 3.1 – Варианты заданий
Продолжение таблицы 3.1
Окончание таблицы 3.1
3.3 Контрольные вопросы 3.3.1 Что представляет собой массив элементов? 3.3.2 Какой максимальной размерности может быть многомерный массив? 3.3.3 Как объявляется массив? 3.3.4 С какой целью используется механизм выделения динамической памяти? 3.3.5 Как инициализируются элементы массива? 3.3.6 Как можно сформировать случайным образом массив элементов? 3.3.7 Какие способами ввода элементов массива существуют в С++? 3.3.8 Приведите алгоритм нахождения максимального значения в каждой строке матрицы произвольного размера. 3.3.9 Каковы особенности обработки квадратной матрицы? 3.3.10 Как организовать обработку матрицы произвольной размерности по столбцам (по строкам)?
Общие сведения Во многих задачах бывает необходимо переставить элементы массива таким образом, чтобы они располагались в порядке возрастания или убывания. Такие массивы называются упорядоченными, а процесс их получения — сортировкой. 4.1.1 Сортировка простым выбором Самым простым алгоритмом является сортировка простым выбором. В сортируемом массиве находится минимальный элемент, который обменивается местами с элементом в начале массива. Оставшаяся часть массива рассматривается как самостоятельный массив, в котором также производится поиск наименьшего элемента и его обмен с первым элементом укороченного массива. Действия повторяются до тех пор, пока массив не укоротится до одного элемента. 4.1.2 Метод пузырьковой сортировки Под пузырьковой сортировкой понимают целый класс алгоритмов сортировки. В своем простейшем варианте пузырьковая сортировка выполняется крайне медленно, поэтому обычно применяют пузырьковую сортировку с элементами оптимизации. Все алгоритмы пузырьковой сортировки имеют общую особенность – обмен элементов производится между двумя соседними элементами массива. Можно уменьшить количество проходов сортировки, выполняя их не (N-1)2 раз, а пока массив не будет отсортирован. Определить этот факт достаточно просто: если массив уже отсортирован, то в процессе прохода в нем не происходит никаких перестановок. Перед началом просмотра нужно установить признак отсутствия перестановок (флаг). В случае, если производится хотя бы одна перестановка, флаг изменяет свое значение. Если к моменту завершения прохода значение флага осталось первоначальным, значит, массив отсортирован и дальнейшие проходы не нужны. Для оптимизации метода пузырьковой сортировки по времени выполнения каждого прохода можно использовать то, что после первого прохода наибольший элемент окажется в конце массива на предназначенном ему месте. В процессе выполнения второго прохода то же самое произойдет со следующим по величине элементом и т.д. Поэтому при последующих проходах можно уменьшать длину просмотра массива, что существенно сократит общее время выполнения алгоритма. Если объединить этот метод оптимизации с проверкой признака завершения сортировки, то получится алгоритм обменной сортировки с признаком завершения. Задание к лабораторной работе Решить задачу, соответствующую варианту, выбранному по таблице 4.1. Построить блок-схему программы и организовать ввод данных, если это необходимо, с помощью генератора случайных чисел. Таблица 4.1 – Варианты заданий
Продолжение таблицы 4.1
Окончание таблицы 4.1
4.3 Контрольные вопросы 4.3.1 Перечислите известные Вам методы сортировки. 4.3.2 В чем заключается суть метода сортировки простым выбором?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.231.245 (0.071 с.) |
 .
.
 , значение частичной суммы которогопри суммировании достаточно большого количества членов приближается к значению π/4.
, значение частичной суммы которогопри суммировании достаточно большого количества членов приближается к значению π/4.
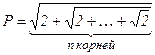 , где n– целое число, введенное с клавиатуры.
, где n– целое число, введенное с клавиатуры.
 .
.
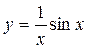 периодической, если аргумент х изменяется в интервале [0;5T], а период Т=2π?
периодической, если аргумент х изменяется в интервале [0;5T], а период Т=2π?



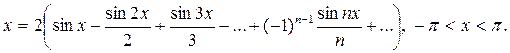

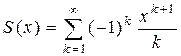 , |x| < 1;
, |x| < 1;
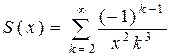 ;
;


 , |x| < 1;
, |x| < 1;









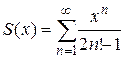
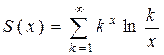



 , |x| < 1;
, |x| < 1;