Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные уравнения и неравенства с двумя неизвестнымиСтр 1 из 3Следующая ⇒
Линейные уравнения и неравенства с двумя неизвестными Уравнением с двумя неизвестными называется выражение вида:
Если из уравнения (1.1) можно выразить переменную
Если уравнение (1.2) имеет вид
то уравнение называют линейным, а графиком этой зависимости является прямая линия. Из элементарной геометрии известно, что через две точки проходит единственная прямая. Это значит, что для построения прямой достаточно знать координаты двух точек, принадлежащих данной прямой. Пример 1. Построить прямую по ее уравнению Решение. Введем систему координат
Рис. 1. Линейным неравенством с двумя неизвестными называют неравенство вида
Точки плоскости Пример 2. Решить неравенство Решение. Построим прямую
Рис. 2. Определим координаты двух точек, принадлежащих прямой: при Матрицы и определители Матрицей порядка Числа, входящие в состав матрицы, называют элементами матрицы. Для обозначения матрицы используют заглавные буквы латинского алфавита
Матрицы одинакового порядка можно складывать и вычитать. Суммой двух матриц
Аналогично определяют разность матриц. Пример 5. Найти сумму и разность матриц
Произведением матрицы
Пример 6. Матрицу Решение. Произведением двух матриц
Замечание 1. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Пример 7. Найти произведение матриц
Решение.
Квадратная матрица Замечание 2. Произведение матриц не обладает свойством коммутативности, то есть в общем случае:
Если Замечание 3. Для обратных матриц справедливо равенство Обратную матрицу принято обозначать Умножение векторов Векторы можно умножать скалярно и векторно. Скалярным произведением двух ненулевых векторов
Эту формулу можно записать в виде
Скалярное произведение имеет следующие свойства: 1. 2. 3. 4. 5. Если 6. Если Упорядоченная тройка векторов
Рис. 7. Векторным произведением вектора Векторное произведение обозначается Векторное произведение имеет следующие свойства: 1. 2. 3. 4. Если 5. Если векторы
Если
Смешанным произведением трех векторов Если заданы координаты векторов в прямоугольной системе координат, то их смешанное произведение вычисляется по формуле:
Свойства смешанного произведения векторов: 1. 2. 3. 4. Пример 11. Даны вершины пирамиды Решение. Вычислим координаты вектора
Угол
1) Площадь грани
2) Объем пирамиды равен одной трети от объема параллелепипеда, построенного на ребрах
3) Длина высоты
Ответ: Комплексные числа Комплексным числом
где
Число Два комплексных числа Два комплексных числа Иногда комплексное число
Угол Аргумент числа Запись числа
Сумма, разность комплексных чисел и умножение определяется так же, как действия над соответствующими векторами. Суммой комплексных чисел
Разностью комплексных чисел
Произведение комплексного числа Произведение двух комплексных чисел
Произведением двух комплексно сопряженных чисел служит действительное число
Деление комплексных чисел определяется, как действие обратное умножению. Частное двух комплексных чисел
Наряду с прямоугольной системой координат
Рис. 8. Из Рис.8 следует, что:
Подставляя
Выражение (9.8) называют тригонометрической формой записи комплексного числа Пусть даны два комплексных числа
Тогда
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются; при делении комплексных чисел их модули делятся, а аргументы вычитаются. Если
Корнем Корень Если
Подставляя в (9.11) значения Пример 12. Дано комплексное число Записать число Решение. Запишем число
Найдем Вычислим
Вычислим
при при при Кроме алгебраической и тригонометрической форм записи комплексного числа
Пусть
Кривые второго порядка 1. Общее уравнение кривых второго порядка. Всякое уравнение второй степени относительно х и у, то есть уравнение вида
где Уравнения кривых можно получить исходя из их геометрических свойств как некоторого геометрического места точек, удовлетворяющего определенным условиям. 2. Окружность. Окружностью называют геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром. Если r – радиус окружности, а точка С(
Если центр окружности совпадает с началом координат, то уравнение окружности имеет простейший – канонический вид: Пример14. Составить уравнение окружности, проходящей через точки Решение. Найдем координаты точки М – середины хорды АВ:
Центр окружности находится на перпендикуляре, восстановленном из середины отрезка АВ. Составим уравнение прямой АВ:
Угловой коэффициент прямой АВ равен -1, следовательно угловой коэффициент перпендикуляра у – 2 = 1(х – 3), или х – у – 1 = 0. Центр окружности С лежит на прямой х + у – 3 = 0 по условию задачи, а также на перпендикуляре х – у – 1 = 0, то есть координаты центра удовлетворяют системе уравнений: х – у – 3 = 0 х – у – 1 = 0. Отсюда х = 2, у = 1, и точка С(2; 1). Радиус окружности равен длине отрезка СА:
Уравнение окружности: (х – 2) 2+(у-1)2 = 10. 3. Эллипс. Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная
Здесь Прямые Пример15. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что его большая ось равна 8, а расстояние между директрисами равно 16. Решение. По условию задачи Так как Уравнение эллипса: Замечание: если в каноническом уравнении эллипса
Пример 16. Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, что расстояние между фокусами 2с = 24, эксцентриситет Решение. Каноническое уравнение эллипса имеет вид: По условию задачи с = 12. так как Так как Уравнение эллипса: 4. Гипербола. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами, есть величина постоянная, равная
Каноническое уравнение гиперболы имеет вид:
где Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки Фокальные радиус-векторы левой ветви гиперболы: Уравнение Пример17. Эксцентриситет гиперболы равен Решение. По определению эксцентриситета, имеем Но Таким образом, уравнение искомой гиперболы имеет вид: Пример 18. Угол между асимптотами гиперболы равен 60 о. Вычислить эксцентриситет гиперболы. Решение. Угловой коэффициент асимптоты гиперболы Подставляя значение углового коэффициента, получим
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.187 (0.186 с.) |
 (1.1).
(1.1). , то получим уравнение вида
, то получим уравнение вида (1.2).
(1.2). или
или (1.3),
(1.3), .
. и определим координаты двух точек, принадлежащих этой прямой: при
и определим координаты двух точек, принадлежащих этой прямой: при  ; при
; при  . Нанесем эти точки на координатную плоскость и проведем через них прямую Рис.1.
. Нанесем эти точки на координатную плоскость и проведем через них прямую Рис.1.





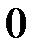
 , где
, где  и
и 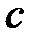 - действительные числа.
- действительные числа. (1.4) расположены на прямой, делящей всю координатную плоскость на две полуплоскости
(1.4) расположены на прямой, делящей всю координатную плоскость на две полуплоскости 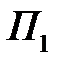 и
и  . В одной из этих полуплоскостей выполняется неравенство
. В одной из этих полуплоскостей выполняется неравенство  , в другой -
, в другой -  .
. и изобразить область решения на плоскости
и изобразить область решения на плоскости 


 ; при
; при  . Нанесем точки на координатную плоскость и построим прямую, проходящую через эти точки. Для определения области решения неравенства, возьмем произвольную точку плоскости, не лежащую на прямой, например
. Нанесем точки на координатную плоскость и построим прямую, проходящую через эти точки. Для определения области решения неравенства, возьмем произвольную точку плоскости, не лежащую на прямой, например  и подставим ее координаты в заданное неравенство:
и подставим ее координаты в заданное неравенство:  , т.е. неравенство не выполняется, следовательно, областью решения заданного неравенства служит полуплоскость, не содержащая точку
, т.е. неравенство не выполняется, следовательно, областью решения заданного неравенства служит полуплоскость, не содержащая точку  . Рис.2.
. Рис.2. называют таблицу чисел, состоящую из
называют таблицу чисел, состоящую из  - строк и
- строк и  - столбцов.
- столбцов. . Элементы матрицы
. Элементы матрицы  обозначают
обозначают  , где
, где  и
и  называют индексом элемента
называют индексом элемента  при
при  , то матрицу называют диагональной. Если у диагональной матрицы все элементы
, то матрицу называют диагональной. Если у диагональной матрицы все элементы  , то матрицу называют единичной матрицей. Единичную матрицу обозначают буквой
, то матрицу называют единичной матрицей. Единичную матрицу обозначают буквой  . Например:
. Например: .
. одинакового порядка называют матрицу
одинакового порядка называют матрицу  того же порядка, элементы которой вычисляют по правилу
того же порядка, элементы которой вычисляют по правилу (3.1).
(3.1). .
. .
.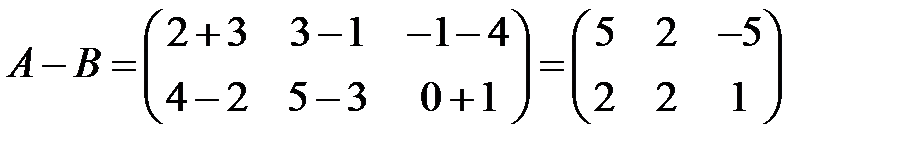 .
. на число
на число  называют матрицу
называют матрицу  , элементы которой вычисляют по формуле
, элементы которой вычисляют по формуле (3.2).
(3.2). умножить на
умножить на  .
. .
. и
и  порядка
порядка  называют матрицу
называют матрицу  порядка
порядка 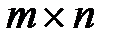 , элементы которой определяют по формуле:
, элементы которой определяют по формуле: (3.3).
(3.3). .
.
 называется обратной матрицей матрицы
называется обратной матрицей матрицы  , если
, если  .
. .
. , то матрицы называют коммутативными.
, то матрицы называют коммутативными. .
. .
. и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: (8.1).
(8.1). .
.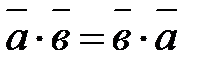 - переместительный закон.
- переместительный закон. - распределительный закон
- распределительный закон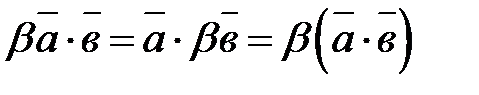
 , отсюда
, отсюда 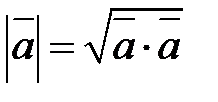
 , то
, то  - условие перпендикулярности векторов
- условие перпендикулярности векторов  ,
,  - вектор силы,
- вектор силы,  - вектор перемещения,
- вектор перемещения,  - работа силы
- работа силы 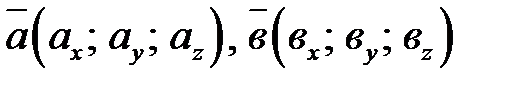 , то
, то  (8.2).
(8.2). называется правой, если кратчайший поворот от вектора
называется правой, если кратчайший поворот от вектора  виден совершающимся против часовой стрелки. Рис.7.
виден совершающимся против часовой стрелки. Рис.7.


 , он перпендикулярен векторам
, он перпендикулярен векторам  и
и  образуют правую тройку.
образуют правую тройку. .
.


 , то
, то 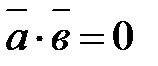
 , где
, где  - площадь параллелограмма, построенного на этих векторах как на сторонах.
- площадь параллелограмма, построенного на этих векторах как на сторонах. и
и  , то:
, то: (8.3).
(8.3). , а
, а  радиус-вектор точки
радиус-вектор точки  равен:
равен: .
. .
. (8.4).
(8.4). - условие компланарности векторов;
- условие компланарности векторов; - объем параллелепипеда, построенного на векторах, как на сторонах;
- объем параллелепипеда, построенного на векторах, как на сторонах; - циклическая перестановка сомножителей не меняет величины смешанного произведения;
- циклическая перестановка сомножителей не меняет величины смешанного произведения;
 . Найти 1) угол между ребром
. Найти 1) угол между ребром  и гранью
и гранью  ; 2) площадь грани
; 2) площадь грани  ; 4) длину высоты, опущенной из вершины
; 4) длину высоты, опущенной из вершины  на грань
на грань  :
: .
. между ребром
между ребром  , образованного перпендикуляром, проведенным к плоскости треугольника
, образованного перпендикуляром, проведенным к плоскости треугольника  . Для нахождения
. Для нахождения  вычислим координаты векторного произведения векторов
вычислим координаты векторного произведения векторов  и
и  :
: ;
; .
. .
. ;
; .
. и
и  , т.е.
, т.е. .
. и
и  . Следовательно
. Следовательно .
. определяется из формулы:
определяется из формулы: ;
;  .
. ;
;  ;
;  ;
;  .
. называется выражение
называется выражение (9.1),
(9.1), и
и  - действительные числа;
- действительные числа; 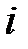 - мнимая единица, определяемая равенством
- мнимая единица, определяемая равенством или
или  (9.2).
(9.2). ;
;  . Если
. Если  , то число
, то число  называют чисто мнимым, если
называют чисто мнимым, если  , то число
, то число  , есть действительное число.
, есть действительное число. называют комплексно сопряженными числами.
называют комплексно сопряженными числами. и
и  считаются равными, если
считаются равными, если  и
и  . Комплексное число
. Комплексное число  , если
, если  и
и  . Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью. , начало которого совпадает с началом координат, соединяющего точку
, начало которого совпадает с началом координат, соединяющего точку  с точкой
с точкой  . Длина этого вектора называется модулем комплексного числа
. Длина этого вектора называется модулем комплексного числа  .
.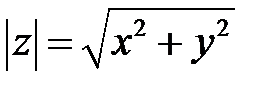 .
. между осью
между осью  и вектором
и вектором  .
. , где
, где  - целое число. Главное значение аргумента числа
- целое число. Главное значение аргумента числа 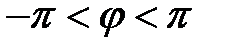 . Главное значение аргумента комплексного числа
. Главное значение аргумента комплексного числа 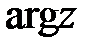 :
:  .
. называют алгебраической формой записи комплексного числа.
называют алгебраической формой записи комплексного числа. и
и  называется комплексное число
называется комплексное число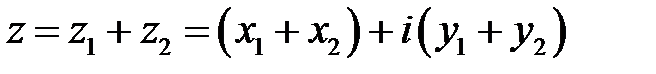 (9.3).
(9.3). (9.4).
(9.4). называется комплексное число
называется комплексное число  .
. и
и  , записанных в алгебраической форме определяется как произведение двучленов:
, записанных в алгебраической форме определяется как произведение двучленов: (9.5).
(9.5). (9.6).
(9.6). (9.7).
(9.7). введем полярную систему, начало которой совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси
введем полярную систему, начало которой совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси  . Рис. 8.
. Рис. 8.



 .
. и
и  в алгебраическую форму комплексного числа, получим
в алгебраическую форму комплексного числа, получим (9.8).
(9.8). , где
, где  .
. и
и  . Записанные в тригонометрической форме:
. Записанные в тригонометрической форме: .
. .
.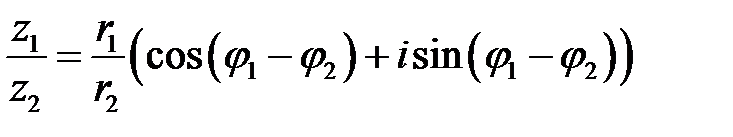 (9.9).
(9.9). - целое положительное число, то из (9.9) следует:
- целое положительное число, то из (9.9) следует: (9.10).
(9.10). называется такое комплексное число
называется такое комплексное число  ,
,  .
. .
.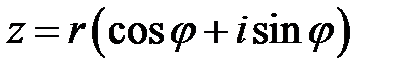 , то
, то  равен:
равен: (9.11).
(9.11). получим ровно
получим ровно  .
. .
. .
. :
:  .
.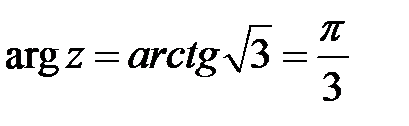 . Тригонометрическая форма записи комплексного числа
. Тригонометрическая форма записи комплексного числа  .
. :
:
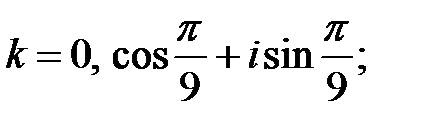


 .
. и
и  , тогда:
, тогда: .
. , (12.1)
, (12.1) - постоянные коэффициенты, причем
- постоянные коэффициенты, причем  , определяет на плоскости линию, которую принято называть кривой второго порядка. Верно и обратное. Существует четыре вида кривых второго порядка: окружность, эллипс, гипербола и парабола. Все они могут быть получены путем сечения конуса плоскостью и потому их еще называют кониками.
, определяет на плоскости линию, которую принято называть кривой второго порядка. Верно и обратное. Существует четыре вида кривых второго порядка: окружность, эллипс, гипербола и парабола. Все они могут быть получены путем сечения конуса плоскостью и потому их еще называют кониками. ) – ее центр, то уравнение окружности имеет вид:
) – ее центр, то уравнение окружности имеет вид: . (12.2)
. (12.2) .
. , то есть М(3; 2).
, то есть М(3; 2). , или х + у – 5 = 0.
, или х + у – 5 = 0. . Уравнение перпендикуляра
. Уравнение перпендикуляра .
. , большая чем расстояние между фокусами. Каноническое уравнение эллипса имеет вид:
, большая чем расстояние между фокусами. Каноническое уравнение эллипса имеет вид: . (12.3)
. (12.3) - большая полуось эллипса,
- большая полуось эллипса,  - малая полуось, причем если расстояние между фокусами равно 2с, то
- малая полуось, причем если расстояние между фокусами равно 2с, то  . Величина
. Величина  называется эксцентриситетом эллипса и характеризует меру сжатия. Так как с <
называется эксцентриситетом эллипса и характеризует меру сжатия. Так как с <  , то
, то  < 1. Расстояния от некоторой точки М, расположенной на эллипсе, до фокусов называются фокальными радиус-векторами этой точки. Фокальные радиус-векторы выражаются через абсциссу точки эллипса по формулам:
< 1. Расстояния от некоторой точки М, расположенной на эллипсе, до фокусов называются фокальными радиус-векторами этой точки. Фокальные радиус-векторы выражаются через абсциссу точки эллипса по формулам:  .
. и
и  называются директрисами эллипса. Директрисы эллипса обладают следующим свойством: если r – фокальный радиус-вектор точки М, d – расстояние от этой точки до односторонней с фокусом директрисы, то
называются директрисами эллипса. Директрисы эллипса обладают следующим свойством: если r – фокальный радиус-вектор точки М, d – расстояние от этой точки до односторонней с фокусом директрисы, то  .
. Уравнение директрис
Уравнение директрис  ; расстояние между директрисами
; расстояние между директрисами  , отсюда
, отсюда  ; так как
; так как  , то
, то  , то есть с = 2.
, то есть с = 2. , то
, то  .
. .
.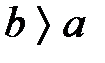 , то фокусы эллипса лежат на оси ординат и
, то фокусы эллипса лежат на оси ординат и  ; уравнения директрис:
; уравнения директрис:  ; фокальные радиус-векторы определяются по формулам:
; фокальные радиус-векторы определяются по формулам:  .
. .
. .
. , то
, то  , то есть
, то есть 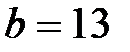 .
. , то
, то  .
. .
. , меньшая, чем расстояние между фокусами (
, меньшая, чем расстояние между фокусами ( ).
). , (12.4)
, (12.4) .
. и
и  называют вершинами гиперболы. Отрезок
называют вершинами гиперболы. Отрезок  называют вещественной осью гиперболы, а отрезок
называют вещественной осью гиперболы, а отрезок  , соединяющий точки
, соединяющий точки  и
и  , - мнимой осью. Гипербола имеет две асимптоты, уравнения которых
, - мнимой осью. Гипербола имеет две асимптоты, уравнения которых  . Отношение
. Отношение  называется эксцентриситетом гиперболы. Прямые, заданные уравнениями
называется эксцентриситетом гиперболы. Прямые, заданные уравнениями  называют директрисами гиперболы. Фокальные радиус-векторы правой ветви гиперболы:
называют директрисами гиперболы. Фокальные радиус-векторы правой ветви гиперболы:  .
. .
. так же является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси OY длины
так же является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси OY длины  . Точки
. Точки  и
и  служат вершинами гиперболы. Ветви гиперболы расположены в верхней и нижней части координатной плоскости. Две гиперболы
служат вершинами гиперболы. Ветви гиперболы расположены в верхней и нижней части координатной плоскости. Две гиперболы  и
и  называют сопряженными гиперболами.
называют сопряженными гиперболами. . Составить простейшее уравнение гиперболы, проходящей через точку М(
. Составить простейшее уравнение гиперболы, проходящей через точку М( ).
). , или
, или  .
. , следовательно
, следовательно  . Так как точка М(
. Так как точка М( ) находится на гиперболе, то
) находится на гиперболе, то  . Отсюда
. Отсюда  .
. .
.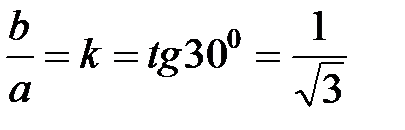 . Эксцентриситет гиперболы
. Эксцентриситет гиперболы  .
. .
.