
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой с угловым коэффициентом ⇐ ПредыдущаяСтр 2 из 2
где Число Уравнение прямой, проходящей через данную точку
Замечание. Уравнением с угловым коэффициентом нельзя задать прямую, перпендикулярную оси Ох. Такая прямая имеет уравнение вида 4. Уравнение прямой, проходящей через данную Даны точка Пусть точка
5. Уравнение прямой, проходящей Пусть точки Возьмем произвольную точку
Уравнений прямой в «отрезках». Пусть точки
Совместное исследование уравнений прямых Пусть даны уравнения двух прямых:
б) Угол между двумя прямыми:
в) Условие параллельности двух прямых:
г) Условие перпендикулярности прямых:
Или д) Условие совпадения двух прямых: Пр. Проверить, будут ли прямые параллельны, перпендикулярны или найти угол меду прямыми и точку их пересечения, построить прямые: Кривые второго порядка. Опр. Кривой 2–го порядка или линией 2-го порядка называется линия, имеющая в ДПСК уравнение 2-й степени относительно x и y:
1. Эллипс (« недостаток» с греч. ) Опр. Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек (фокусов) есть величина постоянная, большая расстояния между фокусами. Получим уравнение эллипса. Для этого введем на плоскости ДПСК так, чтобы фокусы эллипса
Обозначим
Обе части последнего уравнения разделим на
Если в уравнении (7) Если фокусное расстояние эллипса нулевое, т.е.
Опр. Оси симметрии эллипса называются осями эллипса, центр его симметрии (точка пересечения осей) − центром эллипса, точки пересечения эллипса с осями − вершинами эллипса. Опр. Отношение расстояния между фокусами к большой оси называется эксцентриситетом эллипса: Замечание. если если Уравнение эллипса в параметрической форме:
где Параметрическое задание окружности (8):
Опр. Если эллипс задан уравнением (7) и Свойство директрисы: для любой точки эллипса отношение ее расстояния
2. Гипербола (<избыток, преувеличение> с греч.)
Получим уравнение гиперболы. Для этого введем на плоскости ДПСК так, чтобы фокусы гиперболы
Обозначим
Обе части последнего уравнения разделим на
Опр. Если гипербола задана уравнением (9), то число а называется действительной, а Гипербола также может быть задана уравнением
В этом случае а – мнимая, а
Опр. Гипербола, у которой Опр. Прямые Опр. Оси симметрии гиперболы называются осями гиперболы, центр его симметрии (точка пересечения осей) − центром гиперболы. Гипербола пересекает одну из своих осей. Точки пересечения гиперболы с осью называются вершинами гиперболы. Опр. Отношение расстояния между фокусами к длине действительной оси называется эксцентриситетом гиперболы: Замечание. если если Опр. Для гиперболы, заданной уравнением (9), прямые Свойство директрисы: для любой точки гиперболы отношение ее расстояния
3. Парабола ( греч.- приложение )
Получим уравнение параболы. Для этого введем на плоскости ДПСК так, чтобы фокус F оказался на оси Ох и имел координаты
Если оси Ох и Оу поменять ролями, то парабола будет задаваться уравнением
По определению эксцентриситет параболы считается равным 1: Опр. Парабола имеет одну ось симметрии. Эта ось называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Полярная система координат Опр. Полярная система координат определяется заданием: 1) точки О – начала координат (полюс); 2) луча 3) единицей масштаба. При этом поворот полярной оси вокруг полюса против часовой стрелки считается положительным. Углы измеряются в радианах. Опр. Полярным радиусом точки М называется расстояние М от полюса: Опр. Полярным углом точки М называется угол поворота Для задания всех точек плоскости достаточно считать, что Верно и обратное: любая пара значений Связь ПСК с ДПСК. Зададим на плоскости обе системы координат так, чтобы полюс был совмещен с началом ДПСК, ось абсцисс совпадала с полярной осью и единицы масштаба в обеих системах координат имели одинаковую длину. Тогда: 1) если точка М задана полярными координатами
2) если известны декартовы координаты точки
Замечание. Ограничения на полярные координаты
§4. Преобразование декартовых координат Параллельный перенос СК
Таким образом, в системе Поворот СК на плоскости Введем четыре СК:
§ 5. Приведение общего уравнения линии Задача: по общему виду уравнения кривой 2-го порядка определить тип кривой и построить ее. Будем рассматривать только случай, когда В =0, т.е. уравнение линии 2-го порядка имеет вид:
Метод решения данной задачи – выделение полного квадрата: После выделения полного квадрата и перегруппировки слагаемых получим: 1) если 2) если 3) если Сделаем параллельный перенос системы координат:
В новой системе координат уравнение примет канонический вид. С учетом переноса СК, получим одну из следующих кривых:
ПР. Плоскость. Общее уравнение плоскости В ДПСК в пространстве плоскость
Опр. Вектор, перпендикулярный плоскости, называется ее нормалью. Нетрудно установить (см. §1, п.1), что вектор Проведем анализ общего уравнения плоскости (13). Если Если Если Если A =0, B =0, то Если A =0, B =0, Остальные случаи рассмотрите самостоятельно.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.185.194 (0.071 с.) |
 Уравнение прямой, имеющее вид
Уравнение прямой, имеющее вид , (3)
, (3) , называется уравнением с угловым коэффициентом.
, называется уравнением с угловым коэффициентом. называет угловым коэффициентом. Нетрудно установить, что
называет угловым коэффициентом. Нетрудно установить, что  , где
, где 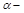 угол наклона прямой к положительному направлению оси Оx.
угол наклона прямой к положительному направлению оси Оx. с данным угловым коэффициентом k имеет вид:
с данным угловым коэффициентом k имеет вид: .
. (см. п.1).
(см. п.1). и вектор
и вектор  . Составим уравнение прямой
. Составим уравнение прямой  .
. . Тогда
. Тогда  . Используя условие коллинеарности векторов, получаем уравнение прямой
. Используя условие коллинеарности векторов, получаем уравнение прямой  :
: . (4)
. (4) . Составим уравнение этой прямой.
. Составим уравнение этой прямой.
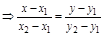 . (5)
. (5) . Составим уравнение прямой через две эти точки:
. Составим уравнение прямой через две эти точки:  . Получаем:
. Получаем: . (6)
. (6) и
и  .
. а) Точка пересечения прямых:
а) Точка пересечения прямых: 
 и
и  . Тогда
. Тогда или
или  .
. или
или  .
. .
. .
. .
.
 .
. ,
,  .
. были расположены на оси Ох симметрично относительно начала координат (см. рис.). Расстояние между фокусами обозначим
были расположены на оси Ох симметрично относительно начала координат (см. рис.). Расстояние между фокусами обозначим  . Возьмем произвольную точку
. Возьмем произвольную точку  , принадлежащую эллипсу. По определению эллипса сумма расстояний от М до
, принадлежащую эллипсу. По определению эллипса сумма расстояний от М до  :
: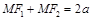 .
.  . Следовательно,
. Следовательно,
 ;
; ;
; .
. . Очевидно, что
. Очевидно, что  .
. .
. .
. . (7)
. (7) Опр. Числа
Опр. Числа  называются полуосями эллипса.
называются полуосями эллипса. , то можно переименовать оси координат. В этом случае фокусы эллипса будут находиться на оси Оу.
, то можно переименовать оси координат. В этом случае фокусы эллипса будут находиться на оси Оу. , то получаем окружность:
, то получаем окружность: (8)
(8) (<эллипс>- <недостаток>).
(<эллипс>- <недостаток>). . Поэтому:
. Поэтому: , то
, то  и эллипс «круглеет»;
и эллипс «круглеет»; , то
, то  и эллипс «сжимается».
и эллипс «сжимается». ,
, угол поворота радиус-вектора точки относительно положительного направления оси Ох.
угол поворота радиус-вектора точки относительно положительного направления оси Ох. .
. называются директрисами эллипса. Если
называются директрисами эллипса. Если 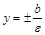 .
. до некоторого фокуса к расстоянию
до некоторого фокуса к расстоянию  до односторонней с этим фокусом директрисы есть величина постоянная, равная эксцентриситету эллипса:
до односторонней с этим фокусом директрисы есть величина постоянная, равная эксцентриситету эллипса: .
. Опр. Гиперболой называется геометрическое место точек, модуль разности расстояний которых от двух данных точек (фокусов) есть величина постоянная, меньшая расстояния между фокусами.
Опр. Гиперболой называется геометрическое место точек, модуль разности расстояний которых от двух данных точек (фокусов) есть величина постоянная, меньшая расстояния между фокусами. :
:  .
. 
 ;
; ;
; .
. . Получим
. Получим .
. . (9)
. (9) мнимой полуосью гиперболы.
мнимой полуосью гиперболы. . (10)
. (10) действительная полуось.
действительная полуось. , называется равнобочной.
, называется равнобочной. называются асимптотами гиперболы.
называются асимптотами гиперболы. (<гипербола>- <избыток>).
(<гипербола>- <избыток>). . Поэтому:
. Поэтому: , то
, то  Опр. Параболой называется геометрическое место точек, равноудаленных от данной точки F (фокуса) и данной прямой d (директрисы)
Опр. Параболой называется геометрическое место точек, равноудаленных от данной точки F (фокуса) и данной прямой d (директрисы)  .
. , а директриса d совпала с прямой
, а директриса d совпала с прямой  , где р – расстояние от фокуса до директрисы. Это расстояние называется параметром параболы. Возьмем произвольную точку
, где р – расстояние от фокуса до директрисы. Это расстояние называется параметром параболы. Возьмем произвольную точку  . Поэтому
. Поэтому ;
; ;
; . (11)
. (11) . (12)
. (12) .
. , исходящего из полюса (полярная ось);
, исходящего из полюса (полярная ось); .
. полярной оси до совпадения с лучом ОМ.
полярной оси до совпадения с лучом ОМ. , а
, а  или
или  . Тогда для каждой точки плоскости, кроме полюса, существует единственная пара полярных координат
. Тогда для каждой точки плоскости, кроме полюса, существует единственная пара полярных координат  . Координаты полюса
. Координаты полюса  ,
,  при
при  определяют единственную точку плоскости. Значение
определяют единственную точку плоскости. Значение  задает полюс.
задает полюс. ;
;
 ,
,
 . Тогда для построения точки
. Тогда для построения точки  в случае
в случае  делается необходимое число полных оборотов полярного луча вокруг полюса, а при
делается необходимое число полных оборотов полярного луча вокруг полюса, а при  от полюса откладывается отрезок длины
от полюса откладывается отрезок длины  на продолжении полярного луча за полюс.
на продолжении полярного луча за полюс. Пусть
Пусть  ,
,  ,
,  ,
,  ,
,  ,
, , тогда
, тогда 
 ,
, ,
, 
 ,
,

 .
. координаты точки
координаты точки  .
. ,
, :
:  .
. :
:  .
.
 =
=  = =
= =  .
. =
=  =
=  .
. .
. (рабочая формула).
(рабочая формула). , то
, то  ;
; , то
, то  ;
; , то
, то  .
. ,
,  .
. – эллипс;
– эллипс;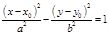 –гипербола;
–гипербола; – парабола;
– парабола; – парабола.
– парабола. . (эл.)
. (эл.) задается уравнением 1-й степени:
задается уравнением 1-й степени: . (13)
. (13) . Таким образом, геометрический смысл коэффициентов общего уравнения плоскости состоит в том, что они дают координаты нормали плоскости.
. Таким образом, геометрический смысл коэффициентов общего уравнения плоскости состоит в том, что они дают координаты нормали плоскости. , то плоскость
, то плоскость  .
.
 , т.к.
, т.к. 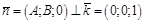 .
. и
и 
 .
. , т.е.
, т.е. 
 .
.


