
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты инерции плоских фигур
В различных математических исследованиях приходится встречаться с определенными интегралами следующих типов:
Все эти интегралы называются моментами инерции площади заданной фигуры относительно координатных осей, а именно:
Таким образом, задача об определении моментов инерции сводится к вычислению определенных интегралов некоторого заданного типа. Процесс такого вычисления может оказаться и весьма трудоемким, но в некоторых случаях эти моменты инерции могут быть найдены сравнительно легко. Найдем осевой момент инерции площади трапеции относительно оси
Элементарная площадь (рис. 2.7,а) Тогда Отрезок Тогда
Частными случаями трапеции являются параллелограмм, прямоугольник, треугольник. Для параллелограмма и прямоугольника (рис. 2.8,а,б) формула имеют вид Для треугольника формулы примут вид: - относительно оси, совпадающей с основанием (рис. 2.8,в) - относительно оси, совпадающей с вершиной (рис. 2.8,г)
Определим центробежный момент инерции для прямоугольника (рис. 2.9,а).
Если оси y и z прямоугольной декартовой системы координат совпадают с двумя сторонами прямоугольника, то центробежный момент инерции площади прямоугольника относительно этих осей будет равен
Приходим к двойному интегралу Для прямоугольного треугольника (рис. 2.9,б).
Так как Подставив полученное значение
Из рисунка имеем Тогда
Полярный момент инерции. Связь с осевыми моментами инерции. Помимо моментов инерции осевых -
Этот интеграл называется полярным моментом инерции относительно полюса Вычислим полярный момент инерции площади круга относительно его геометрического центра (рис. 2.10,б). Элементарную площадку получим следующим образом. Проведем две произвольные окружности с центром в начале координат (полюс Этими четырьмя линиями ограничивается бесконечно малый элемент Тогда
Если элементарную площадку взять в виде кольца радиусом
Между полярным моментом инерции Тогда
Два интеграла в правой части представляют собой осевые моменты инерции Следовательно,
При помощи этой формулы можно вычислить, например, полярный момент инерции площади прямоугольника относительно одной из его вершин и полярный момент инерции площади прямоугольного треугольника относительно вершины прямого угла.
Для прямоугольника (рис. 2.11,а) имеем
Тогда
где Для треугольника (рис. 2.11,б) Тогда
где При помощи формулы
До сих пор рассматривались моменты инерции весьма простых фигур относительно «удобно» расположенных осей. В других более сложных случаях процесс интегрирования, необходимый для определения моментов инерции, оказывается значительно более сложным. В связи с этим, возникает необходимость использования какого-либо приема, позволяющего найти тот или иной момент инерции, пользуясь найденными уже ранее моментами инерции относительно других осей. То есть, необходимо найти зависимость между моментами инерции при преобразовании координатных осей.
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 960; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.239.195 (0.011 с.) |


 (2.4)
(2.4) - осевой момент инерции площади фигуры относительно оси y;
- осевой момент инерции площади фигуры относительно оси y; - осевой момент инерции площади фигуры относительно осиz;
- осевой момент инерции площади фигуры относительно осиz; - центробежный момент инерции площади фигуры относительно двух взаимно перпендикулярных осей y и z.
- центробежный момент инерции площади фигуры относительно двух взаимно перпендикулярных осей y и z. .
.
 . Тогда, согласно формуле
. Тогда, согласно формуле  , имеем двойной интеграл по двум переменным y и z. Представим этот интеграл в виде
, имеем двойной интеграл по двум переменным y и z. Представим этот интеграл в виде  т.е. будем интегрировать сначала по координате y, а затем по z. Получим
т.е. будем интегрировать сначала по координате y, а затем по z. Получим 
 где
где  представляет собой длину горизонтальной элементарной полоски, взятой на расстоянии z от нижнего основания трапеции (от оси y ). Величина эта зависит от координаты z,поэтому ее необходимо предварительно определить. Имеем (рис. 2.7,б)
представляет собой длину горизонтальной элементарной полоски, взятой на расстоянии z от нижнего основания трапеции (от оси y ). Величина эта зависит от координаты z,поэтому ее необходимо предварительно определить. Имеем (рис. 2.7,б) 




 определим из подобия треугольников
определим из подобия треугольников  и
и 
 . Отсюда
. Отсюда  Следовательно.
Следовательно. 
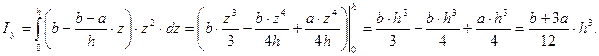

 ;
; .
.

 ;
; 

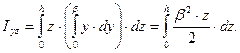
 и
и  .
. 

 и
и 
 то
то 
 и проинтегрировав, получим
и проинтегрировав, получим Определим центробежный момент инерции площади четверти круга относительно его сторон (рис. 2.9,в).
Определим центробежный момент инерции площади четверти круга относительно его сторон (рис. 2.9,в).
 ,
, 

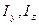 и центробежного
и центробежного  где
где  - расстояние элементарных площадок
- расстояние элементарных площадок  от некоторой точки, которая в частном случае может быть началом координат.
от некоторой точки, которая в частном случае может быть началом координат.
 ( рис. 2.10,а).
( рис. 2.10,а). , а из полюса проведем два бесконечно близких радиуса, составляющих с горизонтальной осью y углы
, а из полюса проведем два бесконечно близких радиуса, составляющих с горизонтальной осью y углы  и
и  .
. .
.
 , то выражение для полярного момента имеет вид
, то выражение для полярного момента имеет вид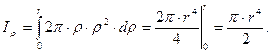
 и осевыми моментами инерции
и осевыми моментами инерции  .
.
 и
и 
 . (2.5)
. (2.5)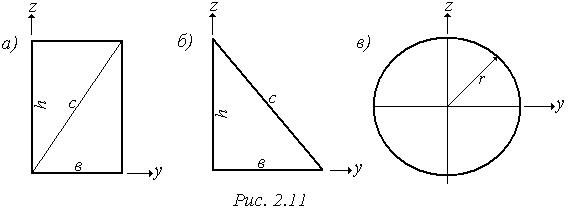

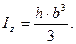

 - площадь прямоугольника, c - его диагональ.
- площадь прямоугольника, c - его диагональ.
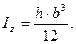

 - гипотенуза треугольника.
- гипотенуза треугольника. можно вычислить осевой момент инерции площади круга относительно одного из его диаметров. Для круга
можно вычислить осевой момент инерции площади круга относительно одного из его диаметров. Для круга 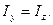 Поэтому
Поэтому 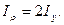 Отсюда
Отсюда



