
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Геометрические характеристики плоских фигур.Стр 1 из 4Следующая ⇒
II. Геометрические характеристики плоских фигур. Статические моменты. Рассмотрим произвольную плоскую фигуру. Плоская фигура – это фигура всеми точками, лежащая в одной плоскости.
Оси этой системы обозначим y и z. Обозначение x оставим для третьей координатной оси, перпендикулярной плоскости чертежа (рис. 2.1). Разобьем площадь фигуры на бесконечное количество бесконечно малых элементов, например, на прямоугольники со сторонами dy и dz параллельными осям координат. Площадь этого бесконечно малого элемента обозначим dA = dy
Эти интегралы называются статическими моментами площади Каждый из интегралов представляет собой сумму произведений элементарных площадок dA на расстояние от соответствующей оси (z или y). Первый интеграл называется статический момент площади сечения относительно оси y, а второй – относительно оси z. Следовательно, для определения статических моментов необходимо найти числовые значения определенных интегралов указанного типа. Рассмотрим примеры.
1. Определить статический момент
Аналогично 2. Найти статический момент площади «уголка» относительно оси y (рис. 2.2,б). Заданная фигура состоит из двух прямоугольников со сторонами b
3. Найти статический момент площади фигуры относительно оси y .( рис. 2.2,в ). Заданную фигуру можно представить образованной путем исключения из прямоугольника с размерами 4. Вычислить статический момент
Имеем Поэтому
Здесь двойной интеграл сводится к двум интегралам с постоянными пределами:
Вычислив каждый интеграл, получим
При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей
Искомые статические моменты будут равны:
или
Таким образом, при параллельном переносе осей статический момент меняется на величину равную произведению площади Ось, относительно которой статический момент равен нулю, называется центральной. Среди семейства параллельных осей она является единственной. Расстояние до этой оси от некоторой, произвольно взятой, оси y1 равно
Аналогично для другого семейства параллельных осей
Полученные выражения дают возможность определить положение центра тяжести, если найдены статические моменты, или найти статические моменты, если известно положение центра тяжести. Если фигура сложная, то ее можно разбить на простые, площадь и центр тяжести, которых легко определяется. Например (рис. 2.5).
Обобщая, полоучим
Некоторую особенность при отыскании центров тяжести представляют симметричные фигуры. Рассмотрим симметричную фигуру (рис. 2.6). Ось симметрии фигуры разбивает заданную фигуру на две одинаковые части (по форме и размерам) I и II, расположенные по разные стороны от этой оси. Примем ось симметрии за координатную ось z, а положение оси y выберем произвольно. При мысленном перегибании всей фигуры по оси симметрииобе части ее совпадут всеми своими точками, в частности, совпадут центры тяжести Тогда
Полученный результат показывает, что центр тяжести площади заданной фигуры лежит на оси z, т.е. на оси симметрии фигуры. Следовательно, если фигура имеет ось симметрии, то центр тяжести лежит на оси симметрии.
Если фигура имеет две или более осей симметрии (квадрат, круг и т.д), то центр тяжести ее лежит на пересечении этих осей. Отсюда следует, что все оси симметрии, независимо от их числа, пересекаются в одной точке.
Главные моменты инерции. Имеем
Сложим и вычтем. Получим
или
Имеем Отсюда Тогда
т.е. Складывая полученные сумму и разность осевых моментов инерции, получим
или
Найдем Имеем
или
Тогда
Верхние знаки берем при Объединяя, получим
Радиусы инерции. Помимо рассмотренных геометрических характеристик плоских фигур, иногда приходится встречаться с еще одной характеристикой – радиусом инерции. Радиусом инерции Так как момент инерции В частном случае главных осей Разделив обе части полученного выражения на площадь фигуры
ли
где
II. Геометрические характеристики плоских фигур. Статические моменты. Рассмотрим произвольную плоскую фигуру. Плоская фигура – это фигура всеми точками, лежащая в одной плоскости.
Оси этой системы обозначим y и z. Обозначение x оставим для третьей координатной оси, перпендикулярной плоскости чертежа (рис. 2.1). Разобьем площадь фигуры на бесконечное количество бесконечно малых элементов, например, на прямоугольники со сторонами dy и dz параллельными осям координат. Площадь этого бесконечно малого элемента обозначим dA = dy
Эти интегралы называются статическими моментами площади Каждый из интегралов представляет собой сумму произведений элементарных площадок dA на расстояние от соответствующей оси (z или y). Первый интеграл называется статический момент площади сечения относительно оси y, а второй – относительно оси z. Следовательно, для определения статических моментов необходимо найти числовые значения определенных интегралов указанного типа. Рассмотрим примеры.
1. Определить статический момент
Аналогично 2. Найти статический момент площади «уголка» относительно оси y (рис. 2.2,б). Заданная фигура состоит из двух прямоугольников со сторонами b
3. Найти статический момент площади фигуры относительно оси y .( рис. 2.2,в ). Заданную фигуру можно представить образованной путем исключения из прямоугольника с размерами 4. Вычислить статический момент
Имеем Поэтому
Здесь двойной интеграл сводится к двум интегралам с постоянными пределами:
Вычислив каждый интеграл, получим
При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей
Искомые статические моменты будут равны:
или
Таким образом, при параллельном переносе осей статический момент меняется на величину равную произведению площади Ось, относительно которой статический момент равен нулю, называется центральной. Среди семейства параллельных осей она является единственной. Расстояние до этой оси от некоторой, произвольно взятой, оси y1 равно
Аналогично для другого семейства параллельных осей
Полученные выражения дают возможность определить положение центра тяжести, если найдены статические моменты, или найти статические моменты, если известно положение центра тяжести. Если фигура сложная, то ее можно разбить на простые, площадь и центр тяжести, которых легко определяется. Например (рис. 2.5).
Обобщая, полоучим
Некоторую особенность при отыскании центров тяжести представляют симметричные фигуры. Рассмотрим симметричную фигуру (рис. 2.6). Ось симметрии фигуры разбивает заданную фигуру на две одинаковые части (по форме и размерам) I и II, расположенные по разные стороны от этой оси. Примем ось симметрии за координатную ось z, а положение оси y выберем произвольно. При мысленном перегибании всей фигуры по оси симметрииобе части ее совпадут всеми своими точками, в частности, совпадут центры тяжести Тогда
Полученный результат показывает, что центр тяжести площади заданной фигуры лежит на оси z, т.е. на оси симметрии фигуры. Следовательно, если фигура имеет ось симметрии, то центр тяжести лежит на оси симметрии.
Если фигура имеет две или более осей симметрии (квадрат, круг и т.д), то центр тяжести ее лежит на пересечении этих осей. Отсюда следует, что все оси симметрии, независимо от их числа, пересекаются в одной точке.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.93.207 (0.156 с.) |

 dz. Возьмем произвольную точку M ( y;z ) и вычислим следующие интегралы:
dz. Возьмем произвольную точку M ( y;z ) и вычислим следующие интегралы:

 . (2.1)
. (2.1) рассматриваемой фигуры относительно координатных осей y и z.
рассматриваемой фигуры относительно координатных осей y и z.
 площади прямоугольника относительно оси y (рис. 2.2,а). Необходимо вычислить интеграл
площади прямоугольника относительно оси y (рис. 2.2,а). Необходимо вычислить интеграл .
. .
. ,h
,h  ,h
,h  Используя результаты предыдущего примера, получим
Используя результаты предыдущего примера, получим
 двух прямоугольников I и II. Тогда
двух прямоугольников I и II. Тогда  , или
, или  .
.


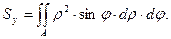
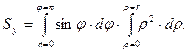
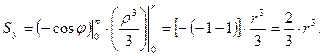
 и
и  ( рис. 2.4 ). Предположим, что площадь сечения
( рис. 2.4 ). Предположим, что площадь сечения  и
и  заданы. Требуется определить
заданы. Требуется определить  и
и  . Из рис.2.4 имеем
. Из рис.2.4 имеем ,
,  .
.

 может быть любой (положительной, отрицательной). Поэтому ее можно подобрать (причем единственным образом) так, чтобы статический момент
может быть любой (положительной, отрицательной). Поэтому ее можно подобрать (причем единственным образом) так, чтобы статический момент 
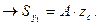
 ,
, 





 (2.2)
(2.2) (2.3)
(2.3) и
и  каждой из частей. Это означает, что точки
каждой из частей. Это означает, что точки  . Отсюда
. Отсюда  Площади обеих частей равны, т.е.
Площади обеих частей равны, т.е. 



 Статический момент любой фигуры тогда и только тогда равен нулю, когда ось проходит через центр тяжести фигуры.
Статический момент любой фигуры тогда и только тогда равен нулю, когда ось проходит через центр тяжести фигуры.



 .
.







 .
.

 ,
,
 (2.16)
(2.16) (2.17)
(2.17) нижние при
нижние при 
 (2.18)
(2.18) площади фигуры относительно оси u называется величина
площади фигуры относительно оси u называется величина  .
. имеет различные значения для разных осей, то и радиус инерции изменяется при переходе от одной оси к другой. Рассмотрим случай, когда все интересующие нас оси проходят через одну и ту же точку. Имеем
имеет различные значения для разных осей, то и радиус инерции изменяется при переходе от одной оси к другой. Рассмотрим случай, когда все интересующие нас оси проходят через одну и ту же точку. Имеем 
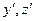
 .
. ,
, , (2.20)
, (2.20) и
и  - радиусы инерции площади заданной фигуры относительно двух главных осей
- радиусы инерции площади заданной фигуры относительно двух главных осей 


