Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Согласованные и подчиненные векторные и матричные нормы.
Определение. Матричная норма ||•||M называется согласованной с векторной нормой ||•||V, если ||A||V≤ ||A||M ||x||V (1) для любой матрицы A и всех векторов x. Определение. Пусть задана векторная норма ||•||V. Тогда числовая функция
называется нормой матрицы, подчиненной (индуцированной ) векторной норме ||•||V. Теорема (Подчиненная векторная норма). Функция (2) определена и является согласованной нормой в Теорема. Для подчиненной матричной нормы справедливо ||Ax||≤||A|x||, ||E||=1 Доказательство
Следствие. Матричная норма ||•||M, подчиненная векторной норме ||•||V, согласована с этой нормой. Матричная норма, подчиненная векторной норме ||•||∞ Получим оценку сверху для величины ||Ax||∞ ||Ax||∞ Покажем, что эта оценка достигается. Пусть максимум по i имеет место при i=l. Возьмем x=(sign(al1),…,sing(aln)). Имеем Таким образом,
Число обусловленности. Определение. Величина
называется числом обусловленности матрицы A по отношению к матричной норме ||•||. Свойства числа обусловленности 10. Для любой матричной нормы cond(A)≥1. 20. Для любой матрицы A и любого числа α выполняется равенство cond(A) =cond(αA). 30. Для спектральной и евклидовой норм число обусловленности не меняется при умножении матрицы слева и справа на любую унитарную матрицу. 40. Для 1-, 2-, ∞-норм и евклидовой нормы число обусловленности не меняется при перестановке строк и столбцов. 50. Для спектральной нормы число обусловленности любой матрицы равно отношению максимального сингулярного числа к минимальному.
Сходимость матриц Определение. Матрица А называется сходящейся, если Лемма. Доказательство . ||Ak||≤||A||k→k→0 0 Теорема. Матрица Доказательство. Пусть Ak→0.Рассмотрим собственный вектор x≠0: Ax=λx. Тогда A2x=A(Ax)=A(λx)=λ(Ax)=λ2x…Akx=λkx→0 Обратно Следствие.
Теорема Гершгорина Теорема Гершгорина и ее следствия. Для произвольной матрицы AЄ
Наиболее полезная и легко применяемая теорема, дающая оценка для собственных значений – теоремы Гершгорина.
Теорема Гершгорина (строчная). Все собственные значения матрицы A заключены в объединении n кругов
Кроме того, если объединение k из этих кругов есть связная область, не пересекающаяся с остальными n−k кругами, то в ней находится ровно k собственных значений матрицы A. Теорема (Гершгорина (столбцовая)). Все собственные значения матрицы AЄ
Кроме того, если k из этих кругов образуют область, изолированную от остальных n-k кругов, то в ней находится ровно kсобственных значений матрицы А.
32. Уточнение оценок собственных значений с помощью преобразования подобия. Если относительно матрицы имеется некоторая дополнительная информация, в силу которой собственные значения принадлежат (или не принадлежат) конкретным множествам, то в сочетании с теоремой Гершгорина эта информация может привести к более точной локализации собственных значений. Определяющие свойства некоторых типов матриц и свойства их собственных значений приведены в таблице
Следствие. Пусть
Пусть
33. Локализация собственных значений Неравенство Шура. Теорема Бендиксона. Теорема (Неравенство Шура). Если A = (aij) ∈
причем равенство имеет место тогда и только тогда, когда матрица А нормальная. Доказательство. Согласно теореме Шура сущ. унитарная матрица
Поскольку след у подобных матриц равен, то trAA∗ =trTT∗ (2) Далее с учётом (2) справедливы соотношения
что и доказывает (1). Равенство возможно тогда и только тогда, когда
Теорема (Бендиксона). Если
Доказательство. Пусть x - нормированный собственный вектор матрицы A, соответствующий собственному значению λk: Ax=λkx, x*x=1. (1). Тогда (Ax)*x=x*A*x=(λkx)*x= Т. к. матр. Bэрмитова, то для нее справедлива теор Рэлея-Ритца:
Отсюда с учетом первого соотношения теоремы Рэлея-Ритца имеем
Аналогично, применяя теоремуРэлея-Ритца к эрмитовой матрице C, получим второе соотношение теоремы.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.252.23 (0.009 с.) |
 (2)
(2)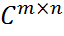 для любых норм в Cm и Cn.
для любых норм в Cm и Cn.

 .
.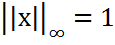 и точные равенства во всей цепочке выше.
и точные равенства во всей цепочке выше. подчиненная векторной норме ||•||∞
подчиненная векторной норме ||•||∞ (1)
(1)
 ||•||: ||A||<1
||•||: ||A||<1  .
. Ak→||•||0
Ak→||•||0  является сходящейся тогда и только тогда, когда
является сходящейся тогда и только тогда, когда  .
. .
. ||
|| 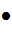 ||:||A||<1
||:||A||<1  Ak→k→∞0
Ak→k→∞0
 - строчная почти-нормы, а также
- строчная почти-нормы, а также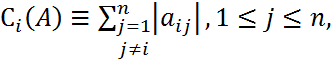 - столбцовые почти – нормы матр. А.
- столбцовые почти – нормы матр. А.
 принадлежат объединению nкругов (столбцовой области Гершгорина)
принадлежат объединению nкругов (столбцовой области Гершгорина)
 .
.




 имеет собственные значения λ1,…,λn, то
имеет собственные значения λ1,…,λn, то
 , такая, что U*AU =T, где T – верхняя треугольная матрица с диагональными элементами tii=λi, i=1,n. Тогда
, такая, что U*AU =T, где T – верхняя треугольная матрица с диагональными элементами tii=λi, i=1,n. Тогда ,а значит
,а значит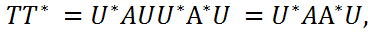 т.е. матрицыAA∗и TT∗подобны.
т.е. матрицыAA∗и TT∗подобны.
 , т.е. тогда итолько тогда, когдаматрицаA– нормальная.
, т.е. тогда итолько тогда, когдаматрицаA– нормальная. ,то
,то

 x*x.(2).
x*x.(2).