
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопряженное пространство и его базис
Пусть Опр. Числовая функция y=f(u) с аргументами из
Опр. Пространство линейных функций, определенных на векторном пространстве Функции из пространства Опр. Вектор u и ковектор f называются ортогональным друг другу, если <f|u>=0. Функционалы Теорема. Координатные функционалы Следствие. Для любого базиса Е пространства Опр. Базис и F={
Ортогональное дополнение сопряженного пространства Опр. Пусть Другими словами, ортогональное дополнение к К тому же, ортогональное дополнение к Теорема. Ортогональное дополнение подпространства Док-во. Пусть Пусть <f|u>== Т.о. произвольный ковектор Так как векторы
Сопряжённое отображение Пусть дано линейное отображение А: Опр. Отображение Теорема. Для любого заданного линейного отображения А сопряженное отображение Докво. Построим отображение Из этого следует, что для данного функционала Т.о. сопряженное отображение определяется как композиция Докажем единственность Пусть Теорема. Пусть А:
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1749; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.150 (0.01 с.) |
 – линейное векторное пространство над полем
– линейное векторное пространство над полем  ,
,  .
. ;
; .
. .
. называются координатными функционалами базиса {
называются координатными функционалами базиса {  }. Для них
}. Для них  (1). Соотношение (1) называются соотношениями биортогональности, а система векторов E={
(1). Соотношение (1) называются соотношениями биортогональности, а система векторов E={  }, удовлетворяющие (1) –биортогональными, что обозначаются как E
}, удовлетворяющие (1) –биортогональными, что обозначаются как E  F.
F. -произвольное подпространство векторного пространства
-произвольное подпространство векторного пространства  :
:  .
.
 .
.
 - произвольный ковектор из ортогонального дополнения. Покажем, что ортогональность ковектора f всем векторам из
- произвольный ковектор из ортогонального дополнения. Покажем, что ортогональность ковектора f всем векторам из  -некоторый базис в
-некоторый базис в 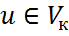 справедливо разложение
справедливо разложение  , и в силу линейности функции f справедливо
, и в силу линейности функции f справедливо . Откуда следует, что <f|u>=0
. Откуда следует, что <f|u>=0 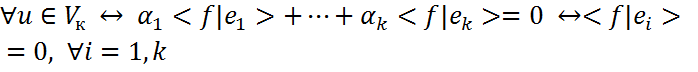 (1)
(1)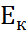 с базисными векторами вида
с базисными векторами вида  система (1) равносильна системе линейных алгебраических уравнений:
система (1) равносильна системе линейных алгебраических уравнений:  (2).
(2). ЛНЗ, то ранг матрицы системы(2) равен k. как известно из линейной алгебры, множество решений системы (2) образует линейное пространство размерности n-k. Это равносильно доказываемому утверждению.
ЛНЗ, то ранг матрицы системы(2) равен k. как известно из линейной алгебры, множество решений системы (2) образует линейное пространство размерности n-k. Это равносильно доказываемому утверждению. →
→  .
. называется сопряженным отображением для А, если для любого
называется сопряженным отображением для А, если для любого  и для любого
и для любого  выполняется следующее соотношение:
выполняется следующее соотношение:  .
. существует, линейно и единственно.
существует, линейно и единственно. удовлетворяющему условию
удовлетворяющему условию  , являющийся образом g при отображение
, являющийся образом g при отображение  .
. на произвольный вектор
на произвольный вектор  . Затем вычисляем значение заданного функционала
. Затем вычисляем значение заданного функционала  . Т.к. выполняются эти условия:
. Т.к. выполняются эти условия: 
 , то можем утверждать, что данное отображение будет линейным.
, то можем утверждать, что данное отображение будет линейным.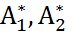 -- два отображения, для которых справедливо
-- два отображения, для которых справедливо  для всех
для всех 
 |u>=0. Фиксируем g и будем менять u. Тогда элемент (
|u>=0. Фиксируем g и будем менять u. Тогда элемент ( . Как линейная функция на
. Как линейная функция на  , что доказывает единственность и завершает доказательство теоремы.
, что доказывает единственность и завершает доказательство теоремы. - биортогональные базисы пространства
- биортогональные базисы пространства  . Тогда если отображение А в базисах Е и Н имеет матрицу А, то сопряженное отображение
. Тогда если отображение А в базисах Е и Н имеет матрицу А, то сопряженное отображение  .
.


