
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная диаграмма гармонических колебанийСтр 1 из 5Следующая ⇒
Таблица аналогий между параметрами поступательного и вращательного движения Кинематика: Поступательное Вращательное S=V0t+ V= a= V=
Динамика:
P=m
Y=
Векторная диаграмма гармонических колебаний Последовательность построения векторной диаграммы колебания, заданного уравнением 1. Выберем на плоскости ось Х, на ней возьмем точку О – начало координат. 2. Под углом α, равном начальной фазе колебаний, к оси Х, из точки О откладываем вектор, равный по длине амплитуде А колебаний. 3. Вектор А равномерно вращаем вокруг точки О против часовой стрелки с угловой скоростью, равной циклической частоте ω0 колебаний. Сложение X(t)=Acos
Графические колебания можно представить в виде с учетом ск.
Начало термодинаки
Количество теплоты идет на изменение температуры и совершение работы самим газом.
1)изотермический T-const 2)изохорный V-const 3)изобарный p-const 4)адиабатный Пружинный маятник Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Период колебаний пружинного маятника х:
Кинематика вращательного движения. Основной кинетической характерной вращательного движения-перемещений явл.элементарный угол поворота d
T
Tg 6.Адиабатный процесс
Количество теплоты
Работа
Энтропия
Динамика поступательного движения. Закона Ньютона в классической механике. Импульст Второй закон Ньютона
Третий закон Ньютона F12 = – F21. Сила гравитационного взаимодействия Кинетическая энергия:
Работа расширение газов
Изохорный работа равна 0.
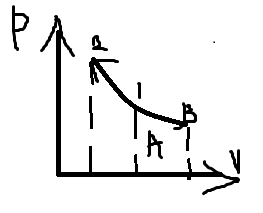
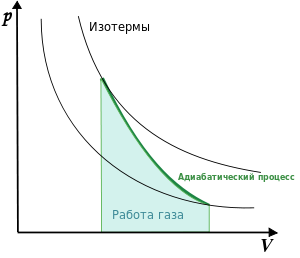
Цикл Карно в pV. Цикл Карно – это замкнутый циклический процесс состоящий из 4 обратимых процессов: 2 изотерм и 2 адиабат.Тело совершающее круговой процесс называется рабочим телом, обменивающийся с другими телами (газ).
Прямой цикл Карно.
А, W, N(p) Для описания процесса изменения энергии тела вводят понятие работы тела.
1. Элемент работы
2. Сила F не совершает работу: А) если Б) если В) если Г) если
Сила F называется потенциальной, если работа этой силы зависит только от начального и конечного положения точки. Работа потенциальной силы равна нулю, не зависит от вида траектории и в замкнутой цепи.
Диссипативные силы – это силы не потенциальные, т.е. зависят от скоростей точек и совершают отрицательную работу при любых перемещениях замкнутых систем.Консервативные – это потенциальные силы.Для характеристики скорости совершения работы вводят понятие мощности.
Потенциальная энергия в системе – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействующих между ними. Взаимодействие между телами осуществляется посредством полей, характеризуется тем, что работа, совершаемая действительными силами при изменении положении тела, не зависит от траектории этого перемещения и равна убыли потенциальной энергии.
Краевой угол.
Поверхностное натяжение. Молекулы поверхностного слоя жидкости обладают большей потенциальной энергией, чем молекулы внутри жидкости.
A=F*
F= A= F* F= Поверхностное натяжение Т=300К
Вещества ослабляющие поверхность натяжения назыв. Поверхностноактивными (мыло, спирт, эфир, нефть). Вещества, увеличивающие поверхность натяжения(сахар, соль). 15.Момент инерции. Ми для шара,конуса Закон сохранения импульса Рассмотрим механическую систему из n материальных точек.2 закон Ньютона F=
Закон сохранения момент импульса.в замкнутой системе момент внешних сил равен 0
II закон ньютона Второй закон ньютона- ускорение приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе мат. Точки.
Импульс (кол-во движения) – векторная вел-на, численно равная произведению массы материальное точки на ее скорость и имеющая направление скорости. Более общая формулировка 2-го закона Ньютона(уравнение движения мат. т.): скорость изменения импульса мат. точки равна действующей на нее силе. Следствие из 2закона Ньютона: принцип независимости действия сил: если на мат. т. Действует одновременно несколько сил, то каждая из этих сил сообщает мат.т ускорение согласно 2 закону Ньютона, как будто других сил не было.
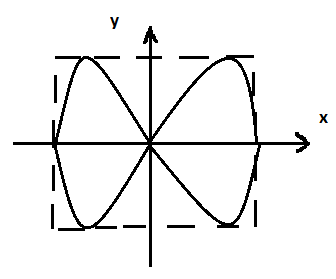
Фигуры Лисажу. X= Ax cos( Y=Ay cos( Если частоты относятся как небольшие целые числа, то фигура замкнута. Фигуры Лиссажу – это замкнутые траектории прочерчиваемые точкой участвующие одновременно в двух взаимно – перпендикулярных колебаний. Форма фигур Лиссажу – зависит от соотношения амплитуд, частоты и разности фаз соназываемых колебаний. 1)
2)
3)
Для чего нужны? Фигуры Лиссажу применяются для опред. Характеристик неизв. Колебаний по второму известному.
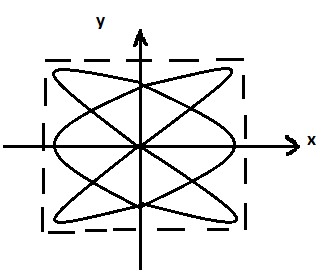
Эффект Доплера. Эффект Доплера – изменение наблюдаемой частоты волны при относительном движении источника и/или наблюдателя. Рассматривается случай, когда скорости источника а) Пусть источник покоится; наблюдатель движется к источнику (рис.4.23).

 Длина волны звука Длина волны звука  . Период колебаний, который воспринимает наблюдатель, это время между прохождением мимо наблюдателя двух последовательных гребней волны: . Период колебаний, который воспринимает наблюдатель, это время между прохождением мимо наблюдателя двух последовательных гребней волны:
б) Пусть источник движется к наблюдателю; наблюдатель покоится. В этом случае изменится длина волны: волны «нагоняют» друг друга за один период на расстояние
Наконец, пусть источник движется от неподвижного наблюдателя. Гребни волн, которые проходят мимо наблюдателя, становятся реже: Объединим все 4 формулы: Верхние знаки относятся к случаю сближения источника и наблюдателя; нижние – удаления.
На боковую поверхность в направлении движения действует касательная сила внутреннего трения
ds - площадь боковой поверхности
На основу цилиндра действует сила разности давления;
Приравниваем эти силы.При стационарном течении суммы двух сил равны нулю.
Цикл Карно В цикле Карно идеальный газ проходит цикл, состоящий из двух адиабат (2-3 и 4-1) и двух изотерм (1-2 и 3-4).1-2 – изотермическое расширение от объёма V1 до V2; при этом газ находится в контакте с нагревателем при температуре T1; 2-3 – адиабатическое расширение от объёма V2 до V3; конечная температура газа равна температуре охладителя T2; 4-1 – адиабатическое сжатие от объёма V4 до V1; конечная температура газа равна температуре нагревателя T1. Для изотермических процессов:
Для адиабатических процессов:
Тогда из последних двух равенств:
Тогда КПД цикла Карно равен:
Сила вязкого трения Вязкость – св-во реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.
Закон подобия.Метод Стокса Если для 2 течений 5 из 6 безмерных комбинаций совпадают,то будут совпадать и 6.Это закон подобия течений.В этом случае жидкость наз. гидродинамически подобными.На некую систему натекает жидкость характерная следующим парам
Число Фруда.Она по порядку величины опр. отношение Wk жидкости к приращению ее,обусловленной работой силы тяжести на харатерной длине.Чем больше число тем больше играет роль инерция по сравнению с тяжестью.Для стационарного течения число Струхале обращается в ∞.В неуживаемых жидкостях число Маха=0. Метод Стокса- метод определения вязкостей основанный на измерении скорости медленно движущихся небольших тел сферической формы.
Таблица аналогий между параметрами поступательного и вращательного движения Кинематика: Поступательное Вращательное S=V0t+ V= a= V=
Динамика:
P=m
Y=
Векторная диаграмма гармонических колебаний Последовательность построения векторной диаграммы колебания, заданного уравнением 1. Выберем на плоскости ось Х, на ней возьмем точку О – начало координат. 2. Под углом α, равном начальной фазе колебаний, к оси Х, из точки О откладываем вектор, равный по длине амплитуде А колебаний. 3. Вектор А равномерно вращаем вокруг точки О против часовой стрелки с угловой скоростью, равной циклической частоте ω0 колебаний. Сложение X(t)=Acos
Графические колебания можно представить в виде с учетом ск.
Начало термодинаки
Количество теплоты идет на изменение температуры и совершение работы самим газом.
1)изотермический T-const 2)изохорный V-const 3)изобарный p-const 4)адиабатный Пружинный маятник Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Период колебаний пружинного маятника х:
|
||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.237 (0.17 с.) |



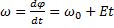
 E=
E= 
 ;
;  ;
; 







 -момент силы
-момент силы -момент импульса
-момент импульса -момент инерции
-момент инерции
 , такова:
, такова: Тогда в любой момент времени угол вектора А с осью Х равен
Тогда в любой момент времени угол вектора А с осью Х равен  . Соответственно проекция конца вектора А на ось Х будет совершать колебания по закону
. Соответственно проекция конца вектора А на ось Х будет совершать колебания по закону 

 расположенным под углом в разной фазе колебаний.
расположенным под углом в разной фазе колебаний.


 => dU=
=> dU=  =>
=> 

 A12<0,A13>0
A12<0,A13>0
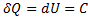 vν(T2-T1)
vν(T2-T1) 


 pν(T2-T1)
pν(T2-T1)  vν(T2-T1)
vν(T2-T1)  2-V1)
2-V1) 
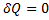
 (T1-T2)
(T1-T2) 







 быстрота изменения этого угла.
быстрота изменения этого угла.  -угловая скорость
-угловая скорость
 ;
;  (векторное)
(векторное) =ab*cos
=ab*cos  (скалярная величина)
(скалярная величина)
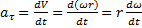

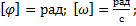









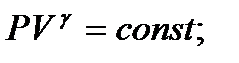

 ;
; 

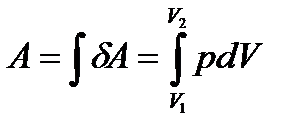














 .
.







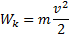
 p-const,
p-const,  =>
=>  =>
=>  => A=
=> A= 
 -изобраный
-изобраный 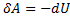



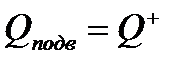





 силы F на малое перемещение
силы F на малое перемещение  точки M приложение силы F называется скалярная величина равная произведению скалярной силы F на перемещение
точки M приложение силы F называется скалярная величина равная произведению скалярной силы F на перемещение 













 Энергия: потенциальная, кинетическая.Кинетическая энергия в механической системе называется энергия механического движения этой системы.Изменение кинетической энергии вызыванием совершением работы.
Энергия: потенциальная, кинетическая.Кинетическая энергия в механической системе называется энергия механического движения этой системы.Изменение кинетической энергии вызыванием совершением работы.





 :
: 







 -вода на стекле.Капля воды растекается,т.е. жидкость смачивает поверхность твердого тела,угол
-вода на стекле.Капля воды растекается,т.е. жидкость смачивает поверхность твердого тела,угол  -острый,угол между касательными и поверхностью тела наз. краевым углом.
-острый,угол между касательными и поверхностью тела наз. краевым углом. ртуть на стекле.сплюснутая капля не смачивая поверхность.угол
ртуть на стекле.сплюснутая капля не смачивая поверхность.угол  (1 точка соприкосновения)Понятие смачивания относительно парафин
(1 точка соприкосновения)Понятие смачивания относительно парафин  вода
вода  смачивание стекло.условие равновесия: -
смачивание стекло.условие равновесия: -  ;
;  -смачивание будет тогда,когда
-смачивание будет тогда,когда  =
=  .
. 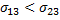 смачивание не происходит
смачивание не происходит
 - поверхностное натяжение, определяется как плотность поверхностной энергии
- поверхностное натяжение, определяется как плотность поверхностной энергии  . Равновесное состояние характеризуется минимальной потенциальной энергией. Если при отсутствии внешних сил жидкость будет стремиться приобретать форму шара. Внутренняя энергия стремиться к минимальной.Так на жидкость стремиться к сокращению площади поверхности, то поверхностный слой представляет собой упругую пленку, в которой действуют силы натяжения.
. Равновесное состояние характеризуется минимальной потенциальной энергией. Если при отсутствии внешних сил жидкость будет стремиться приобретать форму шара. Внутренняя энергия стремиться к минимальной.Так на жидкость стремиться к сокращению площади поверхности, то поверхностный слой представляет собой упругую пленку, в которой действуют силы натяжения.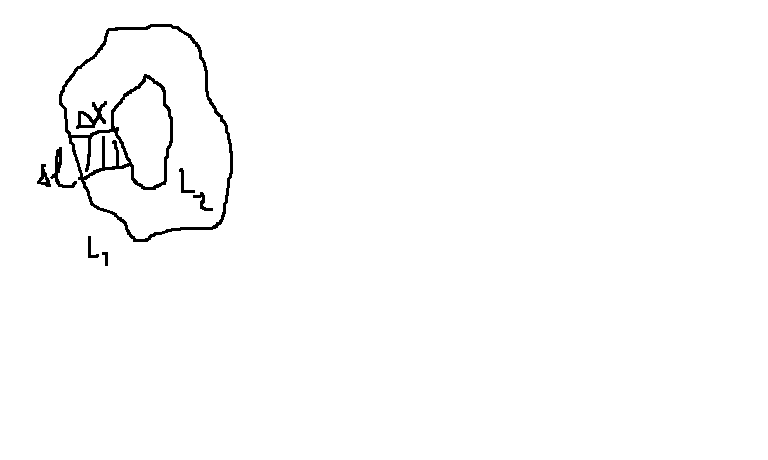


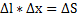



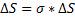
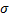
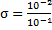



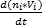 =
= 
 ;
;  сила действующая со стороны т К на т i
сила действующая со стороны т К на т i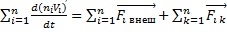 ;
;  -закон сохранения импульса механической системы
-закон сохранения импульса механической системы
 ;
;  ;
; 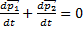 =>
=> 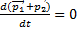 ;
; 
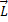 =
=  - момент импульса М=
- момент импульса М= 
 -закон сохранеия момента импульса.
-закон сохранеия момента импульса. ;
; 
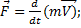

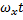 )
) )
) ; где nx и ny это число точек пересечения фигуры с осями ОХ или ОУ или парные им.Условия замкнутости = 𝝂хnx= 𝝂yny
; где nx и ny это число точек пересечения фигуры с осями ОХ или ОУ или парные им.Условия замкнутости = 𝝂хnx= 𝝂yny



 и наблюдателя
и наблюдателя  меньше скорости звука
меньше скорости звука  в данной среде:
в данной среде:  ;
;  . Частота излучения источника
. Частота излучения источника  .
. ;
; 

 .
. . Если наблюдатель движется от источника, то
. Если наблюдатель движется от источника, то  , и
, и  .
. (рис.4.24).
(рис.4.24). . Поскольку
. Поскольку  , то
, то  , и
, и  .
. ; следовательно,
; следовательно, 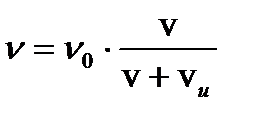 .
. .
. 25. Течение по трубе. Формула Пуазейля.
25. Течение по трубе. Формула Пуазейля.




 R2
R2


 =
= 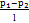
 ;
; 

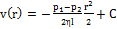

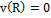



 из этого следует, что При движении от оси трубы скорость меняется по параболическому закону.Рассчитаем расход жидкости – количество жидкости, ежесекундно протекающее через поперечное сечение трубы.
из этого следует, что При движении от оси трубы скорость меняется по параболическому закону.Рассчитаем расход жидкости – количество жидкости, ежесекундно протекающее через поперечное сечение трубы.  ;
;  ;
; 

 - формула Пуазейля(только для ламинарного течения).
- формула Пуазейля(только для ламинарного течения). 3-4 – изотермическое сжатие от объёма V3 до V4; при этом газ находится в контакте с охладителем при температуре T2;
3-4 – изотермическое сжатие от объёма V3 до V4; при этом газ находится в контакте с охладителем при температуре T2;



 ;
; .
.


 .
. Fo-сила вязкого трения.
Fo-сила вязкого трения.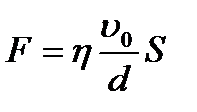 ; η-коэффициент вязкости.
; η-коэффициент вязкости. 

 -[Па*с] [Пз](Пуаз)
-[Па*с] [Пз](Пуаз) .
. . Число Фруда: F=
. Число Фруда: F= 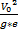 ;Число Маха: M=
;Число Маха: M=  ;Число Струхале: S=
;Число Струхале: S= 

 => Ooy: Fc+FA=mg => Fc=6𝛑ɳrV=>6𝛑ɳrV+ρж g
=> Ooy: Fc+FA=mg => Fc=6𝛑ɳrV=>6𝛑ɳrV+ρж g  ρт g
ρт g  => 3ɳV=2g(ρт - ρж) => ɳ=
=> 3ɳV=2g(ρт - ρж) => ɳ=  (ρт - ρж) => V=
(ρт - ρж) => V=  => ɳ=
=> ɳ=  (ρт - ρж)*t
(ρт - ρж)*t


