
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение действительной функции одной действительной переменной ⇐ ПредыдущаяСтр 2 из 2
Действительная функция - функция, у которой как множество её определений, так и множество её значений являются некоторыми подмножествами множества действительных чисел. Для каждого одного значения x, принадлежащему некоторому множеству по определенному закону ставится в соответствии единственное значение y из множества y; y=f(x).
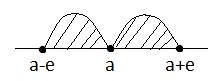
3)Определение окрестности конечной точки, ∞,±∞ Окрестностью конечной точки а принадлежащей R называется любой интервал содержащий а (a-e;a; a+e); e>0, e- окрестность т.а.
Окрестностью +∞ называется (e;+∞); e>0
Окрестностью -∞ называется (-∞;-e); e>0
Окрестностью ∞ называют объединение промежутков (-∞;-e) и (e;+∞); e>0.
Определение сходящейся последовательности Последовательность называется сходящейся, если её предел равен конечному числу.
Определение бесконечно малого и бесконечно большого (БМ и ББ) Последовательность называется бесконечно малым, если её предел равен 0 (обозначается буквами греческого алфавита (α,β,γ)) Последовательность называется бесконечно большой, если её предел модуля |
Определение эквивалентных БМ последовательностей Если
Определение функции, непрерывной в точке Функция y=f(x) называется непрерывной в точке С учетом необходимого и достаточного условия существования предела функции в точке получим:
Функция y=f(x) называется непрерывной в точке
Определение производной функции в точке Пусть функция y=y(x) определена в точке Если существует Функция
Геометрический смысл производной
Уравнение касательной Нормалью называется прямая, перпендикулярная касательной данной точке k данной прямой
Если прямые перпендикулярны, то их угловые коэффициенты связаны равенством: уравнение нормали:
Производная в точке Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.171.121 (0.005 с.) |


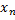 | = +∞
| = +∞ = +∞
= +∞ = 1, то α(x) и β(x) называются эквивалентными БМ при x
= 1, то α(x) и β(x) называются эквивалентными БМ при x 
 и обозначается α(x)
и обозначается α(x)  β(x).
β(x).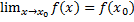
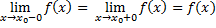
 x
x 
 выбирается так, чтобы
выбирается так, чтобы  рассматриваемой окрестности.
рассматриваемой окрестности. , то его значение называется производной функции в точке
, то его значение называется производной функции в точке 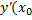 ),
),  учитывая определение приращения аргумента и функции получим, что:
учитывая определение приращения аргумента и функции получим, что: 
 называется дифференцируемой в точке
называется дифференцируемой в точке 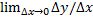 существует и конечен.
существует и конечен.
 ;
;  ;
;



 в этой точке.
в этой точке.


