Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция наиболее часто применяемаяСтр 1 из 2Следующая ⇒
Кафедра ЭТТМ «Эксплуатация транспортных и технологических машин»
ЛИНЕАРИЗАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ и ТЕСТЫ к выполнению лабораторных и практических работ по дисциплинам: «Основы научных исследований», «Методология НИОКР», «Основы методики научных исследований», для студентов специальности 190601,130602,130501 «Автомобили и автомобильное хозяйство» «Машины и оборудование нефтяных и газовых промыслов», «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ» дневной и заочной форм обучения
Сургут 2012 Утверждено учебно-методической комиссией Сургутского института нефти и газа (филиала) Тюменского государственного нефтегазового университета
Составил: доцент, канд. техн. наук Некрасов В.И. Оформление: ст. лаборант Песчанская М.А.
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тюменский государственный нефтегазовый университет», 2012 г. СОДЕРЖАНИЕ
Введение 3 1. Основные сведения 4 1.1. Линеаризация – спрямление 5 1.2.Виды функций 6 2. Порядок выполнения работы11 2.1. Выбор вида функции 15 2.2. Пример степенной функции Y = aXb 18 2.3. Пример показательной функции y = aebх 21 2.4. Пример логарифмической функции 23 2.5. Пример дробной функции 25 3. Тесты 28 Литература ВВЕДЕНИЕ Современный специалист должен: владеть методикой НИ (научных исследований), их планированием и организацией, уметь отбирать и анализировать необходимую информацию, формулировать цель и задачи исследования, обосновывать теоретическую базу, планировать и проводить эксперименты, обрабатывать результаты измерений, оценивать погрешность наблюдений, сопоставлять результаты эксперимента с теоретическими предпосылками, формулировать выводы НИ, составлять отчет, доклад или статью по результатам НИ. Цель лабораторной работы - приобретение практических навыков статистической обработки результатов экспериментальных исследований, в том числе, линеаризацией – спрямлением криволинейных зависимостей. 1. ОСНОВНЫЕ СВЕДЕНИЯ
Для того, чтобы узнать количество опытов - число различных состояний "черного ящика", необходимо число уровней факторов - "р" возвести в степень числа факторов - "k":
N = pk.
При увеличении числа уровней факторов стремительно увеличивается число опытов. Таблица 1.1 Число опытов при различном числе факторов и их уровней
Простая система с пятью факторами на пяти уровнях имеет 55 = 3125 состояний, а для десяти факторов на четырех уровнях необходимо уже более миллиона опытов. Для снижения трудоемкости исследований за счет уменьшения числа опытов необходимо стремиться не только к уменьшению числа факторов, отсеивая несущественные, но и к уменьшению числа уровней, на которых исследуют факторы. Прямолинейные зависимости можно исследовать только на двух уровнях. Криволинейные зависимости необходимо исследовать не менее чем на трех уровнях. 1.1. Линеаризация – спрямление
Многие криволинейные зависимости допускают возможность линеаризации – их спрямления, что позволяет существенно уменьшить число опытов. После преобразования эмпирической формулы к линейной зависимости параметры ее могут быть найдены методом наименьших квадратов (МНК) или другими методами. Когда ни линейная, ни параболическая регрессия не дают желаемой точности приближения, приходится обращаться к другим видам зависимостей: гиперболической, степенной, показательной, логарифмической и др. Но если параметры входят в эмпирическую формулу не линейно, то подбор их МНК связан обычно с громоздкими вычислениями. Поэтому прибегают к специальному методу спрямления этих зависимостей, т. е. сведение этих зависимостей к линейной. Линеаризацией называется преобразование эмпирической формулы y = f (x; a, b) к виду путем подходящей замены переменных. Параметры
а затем уже по ним перечитывают интересующие нас параметры a и b. Виды функций Рассмотрим зависимости, наиболее часто встречающиеся в технических задачах. 1. Зависимость степенного типа. Для отыскания параметров степенной функции (рис. 1.1)
Для перехода к искомой формуле выполним исходные преобразования
Рис. 1.1. График зависимости
На рис. 1.2 изображен график степенной функции
Рис. 1.2. График степенной функции 2. Зависимость показательного типа. Для отыскания параметров показательной функции (рис. 1.3)
Рис. 1.3. График зависимости На рис. 1.4 изображен график показательной функции
Рис. 1.4. График показательной функции 3. Для отыскания параметров функции
Рис. 1.5. График зависимости 4. Для отыскания параметров формулы 5. Зависимости гиперболического типа. Для отыскания параметров гиперболической функции
Рис.1.6. График зависимости Рис.1.7. График зависимости
6. Для отыскания параметров функции применяется преобразование X = x, Y = 1/y и
Рис. 1.8. График зависимости
7. Для отыскания параметров функции (рис. 1.9)
Рис. 1.9. График зависимости
применяется преобразование X = x, Y = x/y и
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Из табл. 2.1 выбрать исходные данные для выполнения работы. Номер варианта (1-й столбец) соответствует номеру фамилии студента в списке журнала группы. Значения Х выделены жирным шрифтом. Значения У приведены по горизонтали в соответствии с номером варианта. Например, для вариантов с 1-го по 10-й: Х1=1; У1=2,15; Х2=3; У2=2,5; Х3 =5; У3=2,8 и т.д.; для вариантов с 11-го по 20-й: Х1=2; У1=11,3; Х2=4; У2=7,9; Х3 =6; У3=6,5 и т.д. 2. Построить график зависимости по исходным данным аналогично рис. 2.1 - 2.3. 3. Из рис. подраздела 1.2. подобрать вид функции, соответствующей построенному графику. 4. Выбирать вид функции используя логарифмическую и полулогарифмическую сетки (рис. 2.4 и 2.5). 5. Определить вид прогрессии. 6. Получить уравнение регрессии, например, методом средних. Примеры обработки данных приведены ниже. 7. Построить график спрямленной зависимости. 8. Обозначить на графиках коэффициенты регрессии. 9. Оценить погрешность спрямления (линеаризации). 10. Оформить отчет по лабораторной работе, который должен содержать: цель работы, полную, аккуратно оформленную информацию о порядке расчетов, графики с обозначениями шкал, коэффициентов регрессии. 11. Ответить на тесты и отчитаться перед преподавателем за выполненную лабораторную работу.
Таблица 2.1 ИСХОДНЫЕ ДАННЫЕ
Рис. 2.1. Исходные данные для спрямления в логарифмических координатах
Рис. 2.2. Исходные данные для спрямления в полулогарифмических координатах
Рис. 2.3. Зависимость объемной температуры масла агрегата трансмиссии от времени непрерывной работы
Выбор вида функции При выборе вида функции, пригодной для спрямления полученной криволинейной эмпирической зависимости можно воспользоваться специальной бумагой (сеткой). Логарифмическая бумага по обеим осям координат имеет логарифмическую шкалу. Полулогарифмическая бумага, как правило, по горизонтали – оси абсцисс имеет равномерную (нормальную) шкалу, а по вертикали – оси ординат – логарифмическую шкалу. Если экспериментальные точки хорошо образуют прямую на логарифмической бумаге (сетке) (рис. 2.4), то выбираем степенную функцию – Y = aXb , если на полулогарифмической (рис. 2.5), то показательную функцию – Y = aebx.
Рис. 2.4. Логарифмическая сетка
Рис. 2.5. Полулогарифмическая сетка Исходные данные для линеаризации приведены в табл. 2.2 и 2.3 и на рис. 2.1 и 2.2 соответственно. Если нет специальной бумаги с необходимой сеткой координат, то определяем тип прогрессии. Для выбора между названными функциями производят два ряда измерений значений функции: для равноотстоящих точек и для точек, образующих геометрическую прогрессию. Затем для каждого ряда измерений вычисляют отношения: Y2 / Y1; Y3 / Y2, … и выбирают тот ряд, для которого эти отношения более постоянны. Если более постоянными оказываются отношения значений для равноотстоящих точек, то выбирают показательную функцию, если между точками, образующими геометрическую прогрессию, то степенную функцию. 2.2. Пример степенной функции Y = aXb
По исходным данным табл. 2.2 строим график – рис. 2.1. Хорошо виден криволинейный характер зависимости. Рассмотрим отношения равноотстоящих точек арифметической прогрессии: Y2 / Y1 = 0,139/ 0,043 = 3,23; Y3 / Y2 = 0,341/ 0,139 = 2,45; Y4 / Y3 =0,637/ 0,341 = 1,87; Y5 / Y4 = 1,068/0,637 = 1,68 и т.д. Отношения систематически существенно убывают, значит, показательная функция не подходит. Вычислим отношения для точек, образующих геометрическую прогрессию со знаменателем прогрессии q = 2. Y5 – Y3 ; 5-3 =2; Y7 – Y5; 7 – 5 = 2. Числитель через 2: 3,5,7,9,11; знаменатель – подряд: 1,2,3,4,5.
Y3 / Y1 = 0,341/ 0,043 = 7,93; Y5 / Y2 = 1,068/ 0,139 = 7,68; Y7 / Y3 = 2,572/ 0,341 = 7,54; Y9 / Y4 = 4,981/ 0,637 = 7,82; Y11 / Y5 = 8,595/ 1,068 = 8,05. Таблица 2.2 Исходные данные и результаты расчетов для степенной функции Y = aXb
N X Y lg X lg Y X3 У = 0,63 Х3 ∆ Y % ∆ Y 1 0,4 0,043 -0,398 -1,367 0,064 0,0403 0,0027 6,2 2 0,6 0,139 -0,222 - 0,857 0,216 0,1361 0,0029 2,1 3 0,8 0,341 -0,097 -0,467 0,512 0,323 0,018 5,3 4 1,0 0,637 0,000 -0,156 1,000 0,630 0,070 1,1 5 1,2 1,068 0,079 0,029 1,728 1,089 -0,021 2,0 6 1,4 1,699 0,146 0,230 2,744 1,729 -0,030 1,8 7 1,6 2,572 0,204 0,410 4,096 2,581 -0,009 0,3 8 1,8 3,646 0,255 0,562 5,832 3,674 -0,028 0,8 9 2,0 4,981 0,301 0,697 8,000 5,040 -0,059 1,2 10 2,2 6,664 0,342 0,824 10,648 6,708 -0,044 0,7 11 2,4 8,595 0,380 0,934 13,824 8,709 -0,114 1,3 Аналогично со знаменателем прогрессии q = 3. Y8 – Y5 ; 8 – 5 = 3; 11 – 8 = 3. Числитель через 3: 5,8,11; знаменатель – подряд. Y5 / Y1 = 1,068/ 0,043 = 24,84; Y8 / Y2 = 3,646/ 0,139 = 26,23;
Y11 / Y3 = 8,595/ 0,341 = 25,21. Отношения приблизительно одинаковы, значит, предпочтительна степенная функция, y = axb , где х – основание степени, точки такой функции хорошо спрямляются на логарифмической бумаге - сетке (рис. 2.4). Определяем среднее значение отношений при знаменателе прогрессии q = 2. (7,93+7,68+7,54+7,82+8,05)/5 =7,806» 8,0. Определяем показатель степени b = lq 7,806/ lq 2 = 0,892/0,301 = 2,963» 3,0. Аналогично, для знаменателя прогрессии q = 3. (24,84 + 26,23 + 25,21)/ 3 = 25,4. b = lq 25,4/ lq 3 = 1,405/0,477 = 2,945» 3,0. Дополняем табл. 2.2 столбцом Х3. Строим график зависимости У от Х3 (рис. 2.6).
Рис. 2.6. Спрямленная зависимость У от Х3
Определяем коэффициент «a» по рис. 2.6. a = tq a = 6,3/10 = 0,63. Получили уравнение степенной функции У = 0,63Х3 Уровень спрямления хороший (последний столбец табл. 2.2) – максимальное отклонение составило 6,2% для первой точки, большинство точек отличается от расчетных значений не более чем на 2%. Это уравнение можно получить методом средних. Составим две группы уравнений по опытам 2-6 и 7-11, используя логарифмические зависимости – 4 -й и 5 -й столбцы. Например, для первого уравнения: lg Y= - 0,857; lg X = - 0,222 (2-й опыт). -0,857 = lg b0 – 0,222 b1 0,410 = lg b0 + 0,204 b1 -0,467 = lg b0 – 0,097 b1 0,562 = lg b0 + 0,255 b1 -0,156 = lg b0 + 0,000 b1 0,697 = lg b0 + 0,301 b1 0,029 = lg b0 + 0,079 b1 0,824 = lg b0 + 0,342 b1 0,230 = lg b0 + 0,146 b1 0,934 = lg b0 + 0,380 b1 -1,221 = 5 lg b0 – 0,094 b1 3,427 = 5 lg b0 +1,482 b1 -1,221 = 5 lg b0 – 0,094 b1 4,648 = 1,576 b1;
b = b1 = 4,648/1,576 = 2,956 ≈ 3,0. 3,427 = 5 lg b0 +1,482 b1; lg b0 = (3,427 – 1,482х3)/5 = - 0,204; а=b0 = 0,625 ≈ 0,63. Y = aXb = 0,63Х3. Коэффициенты полученного уравнения хорошо видны на рис. 2.4. Коэффициент а = 0,63 представлен ординатой от т.1 на оси абсцисс до пересечения с линией регрессии. Угловой коэффициент b = tg α =150/50 = 3,0 определяется по графику как отношение катетов. 2.3. Пример показательной функции y = aebх
Приизучении скорости химической реакции получены данные, приведенные в табл. 2.3 и на рис. 2.2: х = t – время от начала опыта, y – количество вещества. Вычисляем отношения: у2/у1 = 41,9/57,6 = 0,711; 31,0/41,9 = 0,74; 22,7/31 = 0,732; 16,6/22,7 = 0,731; 12,2/16,6 = 0,735; 8,9/12,2 = 0,73; 6,5/8,9 = 0,73. Отношения, кроме первого, изменяются незначительно, имеем арифметическую прогрессию, можно получить уравнение показательной функции y = aebх. Выравнивание производим путем логарифмирования показательной функции y = aebх: ln y = ln a + bt или lg y = lg a + (b/2,303) t.
Таблица 2.3 Исходные данные и результаты расчетов для показательной функции Y = aebx N 1 2 3 4 5 6 7 8 t 3 6 9 12 15 18 21 24 y 57,6 41,9 31,0 22,7 16,6 12,2 8,9 6,5 lg y 1,760 1,622 1,491 1,356 1,220 1,086 0,949 0,813 ln y 4,054 3,735 3,434 3,122 2,809 2,501 2,186 1,872 Yр. 57,86 42,33 30,98 22,68 16,60 12,15 8,89 6,51 ∆y -0,26 -0,43 0,02 0,02 - 0,05 0,01 -0,01 %∆y 0,46 1,03 0,06 0,09 - 0,4 0,11 0,15
Вычисляем значения lg y и наносим на диаграмму точки в координатах (t, lg y). Эти точки хорошо укладываются на прямую линию, что доказывает применимость к данному случаю формулы y = aebх. Спрямление исходных данных табл. 2.3 представлено на полулогарифмической сетке рис. 2.5. Коэффициенты уравнения регрессии можно определить по рис. 2.5: а = b0 =79 – это отрезок от начала координат до точки пересечения линии регрессии с осью ординат. b1 = tg α = (lg10 – lg79)/20 = (1,0 – 1,898)/20 = - 0,045. tg α определяем как отношение катетов: противолежащий – это разность между точками 10 и 79 на оси ординат, прилежащий – отрезок 20 на оси абсцисс, соответствующий этим точкам. b = b1/ lg e = - 0,045/0,434 = - 0,1037. Через натуральные логарифмы(5-я строка табл. 2.3) b = (ln 6,5 – ln 57,6)/(24-3) = (1,872 – 4,054)/21 = -0,104. Получили уравнение показательной функции y = 79e- 0,104х. Используем метод средних. Разбиваем 8 пар измерений на две равные группы и составляем для каждой группы по 4 условных уравнения вида ln у = ln а + bх: 4,054 = ln а + 3b 2,809 = ln а + 15b 3,735 = ln а + 6b 2,501 = ln а + 18b 3,434 = ln а + 9b 2,186 = ln а + 21b 3,122 = ln а + 12b 1,872 = ln а + 24b 14,345 = 4 ln а + 30b 9,368 = 4 ln а + 78b 9,368 = 4 ln а + 78b 4,977 = - 48 b; b = 4,977/(-48) = - 0,1037. 9,368 = 4 ln а + 78b; ln а =[9,368 – 78х (-0,1037)]/4 = 0,31985, а =78,57. Получили уравнение y = 79e- 0,104х. Другой вид этой зависимости lg y = lg 79 – 0,045 х = 1,9 – 0,045 х. Например, при х=9, lg y = 1,9 – 0,045х9 = 1,495; y =31,28. Результаты расчетов по уравнению 2.2 приведены в 6 -й строке табл. 2.3. Совпадение результатов высокое – 8 -я строка. Пример логарифмической функции На рис. 2.3 приведены две криволинейные зависимости, полученные при исследовании теплового состояния трансмиссионных агрегатов. Верхняя зависимость представлена в табл. 2.4. Полулогарифмическая сетка и спрямленные зависимости от рис. 2.3 показаны на рис. 2.7. В отличие от рис. 2.5 логарифмическая шкала по оси абсцисс, а не оси ординат. На рис. 2.7 коэффициенты уравнения регрессии представлены как разница между ординатами на уровне τ = 100 и τ = 10. b1 = ∆t = 107 – 37 = 70. b0 = 37 – 70 = - 33. b0 – это разность между условным b0, указанным на рис. 2.7 как отрезок от начала координат до ∆t = 37 при τ = 10 и b1. Фактическиискомое b0 расположено ниже и левее на интервал, равный ранее указанному. Получили уравнение ∆t = 70 lg τ – 33.
Рис. 2.7. Спрямление зависимостей рис. 2.3 на полулогарифмической сетке Таблица 2.4 Исходные данные и результаты расчетов N τ, мин lg τ ln τ tэ.,0С ln tэ tр.,0С ∆t % ∆t 1 10 1,000 2,303 37 3,611 37 0,0 0,0 2 20 1,301 2,996 58 4,060 58,07 -0,07 0,12 3 40 1,602 3,689 79 4,369 79,14 -0,14 0,18 4 60 1,778 4,094 92 4,522 91,46 0,54 0,59 5 80 1,903 4,382 101 4,615 100,21 0,79 0,78 6 100 2,000 4,605 107 4,673 107,00 0,0 0,0 7 120 2,079 4,787 113 4,727 112,53 0,47 0,42 8 140 2,146 4,942 117 4,762 117,22 -0,22 0,19 9 160 2,204 5,075 122 4,804 121,28 0,72 0,59 10 180 2,255 5,193 126 4,836 124,85 1,15 0,91 11 200 2,301 5,298 129 4,860 128,07 0,93 0,72
Результаты расчетов по этой зависимости и сравнение с исходными данными приведены в последних столбцах табл. 2.4. Коэффициенты спрямленной функции можно получить методом средних. Составим две группы уравнений по опытам 2-6 и 7-11. 58 = b0 + 1,301b1 113 = b0 + 2,079b1 79 = b0 + 1,602b1 117 = b0 + 2,145b1 92 = b0 + 1,778b1 122 = b0 + 2,204b1 101 = b0 + 1,903b1 126 = b0 + 2,255b1 107 = b0 + 2,000b1 129 = b0 + 2,301b1 437 = 5b0 +8,584 b1 607 = 5b0 +10,984b1 437 = 5b0 +8,584b1 170 = 2,4 b1; b1 =170/2,4 = 70,8; 607 = 5b0 +10,984х70,8; b0 = (607 – 778)/5 = -34,2; Для второй зависимости на рис. 2.3 (рис. 2.7): b1 = ∆t = 67 – 23 = 44; b0 = 23 – 67 = - 21; получили уравнение ∆t = 44 lg τ – 21. Пример дробной функции Хорошие результаты обеспечивает спрямление заменой Y = х/у (табл. 2.5 и рис. 2.8). Таблица 2.5 Исходные данные и результаты расчетов спрямления заменой Y = х/у N τ, мин tэ.,0С Y = х/у tр.,0С ∆t % ∆t 1 20 33,4 0,599 31,40 2,00 6,00 2 40 47,1 0,849 47,22 -0,13 0,27 3 60 56,5 1,062 56,76 0,26 0,47 4 80 62,5 1,280 63,14 -0,64 1,03 5 100 67,2 1,488 67,70 -0,50 0,75 6 120 70,8 1,695 71,13 -0,33 0,47 7 140 73,5 1,905 73,80 -0,30 0,41 8 160 76,1 2,102 75,94 0,16 0,21 9 180 78,0 2,308 77,69 0,31 0,40 10 200 79,7 2,509 79,15 0,55 0,70
Рис. 2.8. Спрямление заменой Y = х/у Для определения коэффициентов уравнения регрессии применим метод средних. 0,599 = а + 20 b 1,695 = а + 120 b 0,849 = а + 40 b 1,905 = а + 140 b 1,062 = а + 60 b 2,102 = а + 160 b 1,280 = а + 80 b 2,308 = а + 180 b 1,488 = а + 100 b 2,509 = а + 200 b 5,278 = 5а + 300 b 10,519 = 5а + 800 b 5,278 = 5а + 300 b 5,241 = 500 b; b = 5, 241/500= 0,01048. 10,519 = 5а + 800 b; а = (10,519 – 800х0,01048)/5 = 0,427. Получили уравнение Y = 0,427 + 0,0105 х; у = х/(0,427 +0,0105 х). tр = τ/(0,427 +0,0105 τ). Коэффициенты уравнения можно определить по графику рис. 2.8. а = b0 = 0,43 – отрезок от начала координат до пересечения оси ординат с линией регрессии. b = b1 = (2,52 – 0,43)/200 = 0,0105. Это отношение противолежащего катета, равного ординате т.10, минус b0, к прилежащему катету, равному отрезку от 0 до 200 по оси абсцисс.
Как было отмечено ранее, методы линеаризации дают лишь приближенные результаты, поскольку параметры найденные этими методами обращают в минимум сумму квадратов отклонений значений преобразованных величин Y от расчетных значений, а не сумму квадратов отклонений измеренных величин y от соответствующих расчетных. Другими словами, найденные значения параметров не будут удовлетворять принципу наименьших квадратов и могут служить только в качестве первого приближения к наилучшим оценкам отыскиваемых параметров. Один из приемов линеаризации использован при исследовании теплового состояния трансмиссионного агрегата для фактора х2. τ – время непрерывной работы агрегата используется в логарифмическом виде. Верхний уровень фактора lg 200 = 2,301; нижний уровень – lg 20 = 1,301. Линеаризация позволила использовать ПФЭ 23 – опыты в 8-ми точках факторного пространства на двух уровнях для трех факторов. Для подобного исследования на трех уровнях потребуется 27 опытов. ТЕСТЫ Для линеаризации? 1. Логарифмическая. 2. Тригонометрическая. 3. Дифференциальная. 4. Интегральная Цель линеаризации? 1. Увеличить число уровней до 4. 2. Увеличить число уровней до 5. 3. Уменьшить число уровней до 2. 4. Уменьшить число уровней до 3. Криволинейной функции? 1. Не менее 2. 2. Не менее 3. 3. Не менее 4. 4. Не менее 5. 7. Обозначения букв в формуле N = pk? 1: k - количество опытов; р - число уровней факторов; N – число факторов; 2: р - количество опытов; N - число уровней факторов; k – число факторов; 3: N - количество опытов; р - число уровней факторов; k – число факторов; 4: N - количество опытов; k - число уровней факторов; р – число факторов; Какая функция спрямляется в Логарифмической сетке? Какая функция спрямляется в Полулогарифмической сетке? 1 – степенная; 2 – гиперболическая; 3 – показательная; 4 – дробная. 14.Название функции Y = aXb? 15. Название функции Y = aebx? 1 – дробная; 2 – показательная;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.244 (0.266 с.) |
и 
преобразованной формулы находят по формулам МНК:
,
,
применяют логарифмическое преобразование 
и замену X = ln x, Y = ln y, что дает 
, где 
.
.
в декартовой системе координат и в логарифмических координатах.
применяют логарифмическое преобразование 
и замену X = x, Y = ln y, что снова приводит к линейной зависимости с 
, 
.
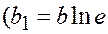в декартовой системе координат и в полулогарифмических координатах.
(рис. 1.5) применяется преобразование X = 1/x, Y = ln y и 
(рис. 1.6) применяют преобразование 
и 
.
(рис. 1.7) применяется преобразование Y = y, X = 1/x и 
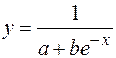
(рис. 1.8)
.
, 
.
