З використанням Microsoft Excel

 

 

Навчальний посібник

до самостійної роботи з

прикладної механіки

 

 

Дніпропетровськ 2006

 

 

Навчальний посібник “Розрахунок кінематичних характеристик точки з використанням Microsoft Excel” / Дніпроп. держ. агр. ун-т. Дніпропетровськ, 2006, 18 с. Тираж – 30

 

 

Складено для студентів денної та заочної форми навчання зі с спеціальностей “Екологія навколишнього середовища“, “Садово-паркове господарство”, “Зберігання та переробка продукції”.

 

Посібник містить в собі варіанти індивідуальних завдань. Наведено приклад визначення кінематичних характеристик руху точки з використанням Microsoft Excel.

 

Укладачи:

доц. Гасюк Л.І.,

ас. Гурідова В.О.,

доц. Науменко М.М.,

доц. Швайко В.М.

 

 

Рецензенти: д.т.н., проф. Колесник І.А. (Національна металургійна академія)

к ф.-м.н., проф. Ільїн Р.П.

 

 

Рекомендовано на засіданні кафедри теоретичної механіки

і опору матеріалів. Протокол № 6 від 07.04.2006 р.

 

Затверджено на засіданні науково -

методичної ради еколого-меліоративного факультету

Протокол № 9 від 04.05.2006 р.

 

I. КІНЕМАТИКА ТОЧКИ

 

Визначення швидкості і прискорення точки за заданими рівняннями її руху

 

За заданими рівняннями руху точки М встановити вид її траєкторії (зобразити її графічно) і для моментів часу t_k = k × Dt (k = 0, 1... 6, Dt = 1 сек) знайти її швидкості, повні, дотичні і нормальні прискорення (побудувати графічні залежності), а також радіуси кривизни траєкторії у відповідних точках (знайти його максимальне значення).

Необхідні дані наведені в табл|. 1.1.

Таблиця 1.1

№№	x = x (t), м	№№	y = y (t), м
	5 + sin (π t / 6)		5 + 2 cos (π t / 6)
	5 + 2 sin (π t / 6)		1 + cos (π t / 6)
	5 + sin (π t / 6)		- 1 + cos (π t / 6)
	2 + sin (π t / 6)		4 + 3 cos (π t / 6)
	3 + 6 sin (π t / 6)		3 + 2 cos (π t / 6)
	2 + 3 sin (π t / 6)		4 + cos (π t / 6)
	- 5 + sin (π t / 6)		2 + 3 cos (π t / 6)
	2 - 3 sin (π t / 6)		2 + 4 cos (π t / 6)
	6 - 3 sin (π t / 6)		2 + 3 cos (π t / 6)
	1 - 3 sin (π t / 6)		2 + cos (π t / 6)
	5 - 2 sin (π t / 6)		4 - 3 cos (π t / 6)
	2 - sin (π t / 6)		- 3 + 2 cos (π t / 6)
	- 2 + 3 sin (π t / 6)		2 cos (π t / 6)
	3 sin (π t / 6)		4 - cos (π t / 6)
	5 - sin (π t / 6)		- 4 + cos (π t / 6)
	3 - 2 sin (π t / 6)		cos (π t / 6)
	2 sin (π t / 6)		- 2 + 3 cos (π t / 6)
	3 - 6 sin (π t / 6)		- 2 + 4 cos (π t / 6)
	4 sin (π t / 6)		2 - 3 cos (π t / 6)
	- 1 + 3 sin (π t / 6)		- 2 + cos (π t / 6)

 

Всі обчислення і побудови проводяться в інтегрованій комп'ютерній системі Microsoft Excel.

 

 

Приклад виконання.|

 

Варіант: №№ - ****; №№ - **** Табл. 1.1

 

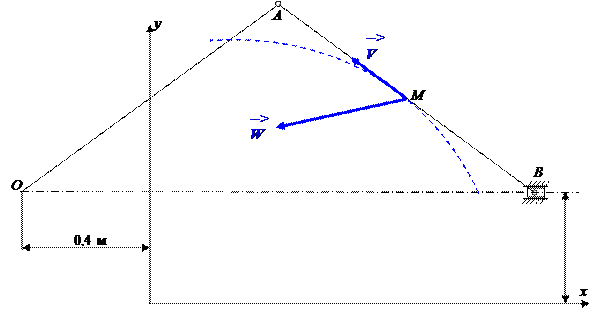
Рух точки М шатуна кривошипного механізму (рис. 1.1) в площині ху заданий рівняннями

 

x = x₀ + x_c cos (πt / 6) = - 0.4 + 1.2 cos (π t / 6)

(1.1)

y = y₀ + y_s sin (π t / 6) = 0.4 + 0.4 sin (π t / 6)

 

 

 

 

Рис. 1.1

 

Розв’язок

Зведена таблиця початкових даних

 

x0	xc	y0	ys
-0,4	1,2	0,4	0,4

 

Рівняння руху (1.1) є параметричними рівняннями траєкторії точки М. Для визначення рівняння траєкторії точки в координатній формі необхідно виключити з (1.1) час t.

Тоді

[ (x - x₀) / x_c ]² + [ (y - y₀) / y_s ]² = 1 (1.2)

або

[ (x + 0.4) / 1.2 ]² + [ (y - 0.4) / 0.4 ]² = 1

 

Це рівняння є рівнянням еліпса.

Переходимо до визначення швидкості точки М. Проекції цієї швидкості дорівнюють першим похідним від координат за часом

 

V_x = x ' = - (π / 6) × x_c × sin (π t / 6) = - 0.628 × sin (π t / 6) м/сек

(1.3)

V_y = y ' = (π / 6) × y_s × cos (πt / 6) = 0.209 × cos (πt / 6) м/сек

 

При отриманні числових коефіцієнтів необхідно скористатися майстром функцій f_x або визвати меню Вставка ==> Функция….

 

Модуль швидкості визначається за формулою

 

V = (V_x ² + V_y ²)^1/2 (1.4)

 

Направляючі косинуси вектора швидкості будуть дорівнювати

 

 

Ù Ù

cos (V, x) = V / V_x, cos (V, y) = V / V_y.

 

Переходимо до визначення прискорення точки. Проекції прискорення дорівнюють

 

W_x = x '' = - (π / 6)² × x_c × cos (πt / 6) = - 0,329 × cos (πt / 6) м/сек²

(1.5)

W_y = y '' = - (π / 6)² × y_s × sin (πt / 6) = - 0,110 × sin (πt / 6) м/сек²

 

Модуль прискорення точки

W = (W_x ² + W_y ²)^1/2 (1.6)

 

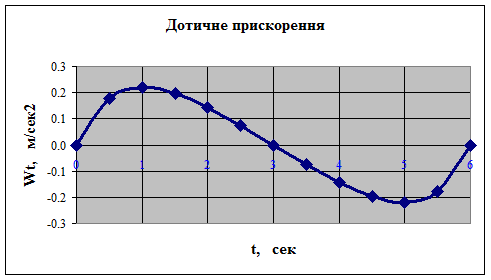
Дотичне прискорення знаходимо шляхом диференціювання модуля швидкості (1.4):

 

W_t = | dV / dt | = (V_x · W_x + V_y · W_y) / V (1.7)

 

Знак " + " при dV / dt показує, що рух точки є прискореним і, отже, напрямок векторів W_t і V збігається. Нормальне прискорення точки обчислюється за формулою

 

W_n = (W ² - W_t ²)^1/2 (1.8)

 

Радіус кривизни траєкторії визначається

 

r = V ² / Wn (1.9)

 

На підставі формул (1.1), (1.3) - (1.9), з використанням функцій Microsoft Excel, знаходимо координати точки, її швидкість, прискорення і їх проекції, а також радіуси кривизни для заданих моментів часу.

Масив значень приведений в табл. 1.2.

Таблиця 1.2

 

t,сек		1,0	2,0	3,0	4,0	5,0	6,0
x,м	0,800	0,639	0,200	-0,400	-1,000	-1,439	-1,600
y,м	0,400	0,600	0,746	0,800	0,746	0,600	0,400
Vx,м/сек	0,000	-0,314	-0,544	-0,628	-0,544	-0,314	0,000
Vy,м/сек	0,209	0,181	0,105	0,000	-0,105	-0,181	-0,209
| V |, м/сек	0,209	0,363	0,554	0,628	0,554	0,363	0,209
Wx,м/сек^2	-0,329	-0,285	-0,164	0,000	0,164	0,285	0,329
Wy,м/сек^2	0,000	-0,055	-0,095	-0,110	-0,095	-0,055	0,000
W, /сек^2	0,329	0,290	0,190	0,110	0,190	0,290	0,329
Wt,м/сек^2	0,000	0,219	0,144	0,000	-0,144	-0,219	0,000
Wn,м/сек^2	0,329	0,190	0,124	0,110	0,124	0,190	0,329
r,м	0,133	0,693	2,469	3,600	2,469	0,693	0,133

 

 

Послідовно викликаючи меню Вставка ==> Диаграмма … ==> Точечная або Мастер диаграмм і т.д., одержуємо наступні графічні залежності:

 

 

 

 

 

 

 

 

 

 

Максимального значення радіусу кривизни траєкторії набуваємо на підставі даних, що представлені в останньому рядку табл. 1.2. з використанням функції МАКС():

 

r_max = 3,600 м,

 

При виконанні завдання, необхідно використовувати наступні функції Microsoft Excel:

ПИ(), COS(), SIN(), СТЕПЕНЬ(;2), КОРЕНЬ(), МАКС().