
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение материальной точки в поле силы тяжести Земли
Закон всемирного тяготения является одним из фундаментальных законов природы. Как известно, все тела притягиваются друг к другу, сила притяжения двух тел определяется:
где γ – гравитационная постоянная; m 1 и m 2 – массы тел; r – расстояния между центрами масс двух притягивающихся тел. Скалярная форма записи закона всемирного тяготения удобна для расчета гравитационных сил между двумя тела. При расчете сил притяжения между системой тел, выражение (29) удобно переписать в векторной форме и считать силу притяжения остальных тел относительно данного, на центр масс которого надо поставить начало координат:
Как известно, у поверхности Земли все тела, в отсутствии силы аэродинамического сопротивления, падают на Землю с постоянным ускорением Частным случаем движения в поле силы тяжести Земли является задача вычисления космических скоростей. Первой космической скоростью называют скорость, с которой нужно бросить тело параллельно поверхности Земли у ее поверхности, чтобы тело двигалось по окружности стало спутником Земли. Второй космической скоростью называют скорость, с которой нужно бросить тело вертикально вверх, чтобы тело, преодолев поле силы тяжести Земли, на Землю никогда не вернулось. При вычислении космических скоростей используют следующие допущения: 1. Землю считают покоящимся шарообразным телом. 2. Отсутствуют силы аэродинамического сопротивления. 3. Запускаемое тело пренебрежимо мало по сравнению с Землей, и его можно считать материальной точкой. Первая космическая скорость вычисляется из условия, что центростремительное ускорение искусственного спутника Земли равняется ускорению свободного падения:
где Вторая космическая скорость вычисляется из закона сохранения механической энергии: кинетическая энергия брошенного тела массой m идет на преодоление работы поля силы тяжести Земли с ее поверхности на бесконечность::
Дальнейший ход вычислений следующий::
Следует отметить, что впервые космические скорости были достигнуты в СССР в 60-х годах XX века успешными запусками искусственных спутников Земли и Солнца. Единственным способом равноускоренного движения тела в безвоздушном пространстве является реактивное движение. При реактивном движении тело отталкивается от части собственной массы выбрасывая ее в противоположную сторону. Примерами реактивного движения являются: отдача ружья, движение лодки от берега, при сходе пассажира на берег, полет ракеты и реактивного самолета. Реактивный ракетный или самолетный двигатель отталкивает ракету или самолет, выбрасывая из себя через сопло поток раскаленного сгоревшего топлива. Поэтому для достижения максимальной силы тяги двигателя теплота сгорания топлива в окислителе должна быть наибольшей. Для этого используют высококалорийные пары топливо плюс окислитель: керосин и кислород воздуха, керосин и азотная кислота, водород и кислород, метан и кислород, ракетные пороха. Расходы топлива на старте космической ракеты достигают значений до 10 т/с. Впервые вывод уравнения динамики движения тела переменной массы (реактивного движения) был проведен русским ученым И.В.Мещерским из закона сохранения импульса. Изменение за малое время dt импульса
Здесь m и
или
где
Векторная величина
имеет размерность силы и называется реактивной силой. К.Э.Циолковский полагая в уравнении Мещерского
где
Интегрируя последнее уравнение с подстановкой начальных условий, что стартовая масса ракеты m 0, а конечная m 0– mТ, где mТ – масса топлива с окислителя, получим формулу Циолковского:
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.133.148 (0.005 с.) |
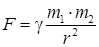 .
.
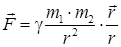 .
.
 и сила тяжести у поверхности земли пропорциональна массе притягиваемо к земле тела:
и сила тяжести у поверхности земли пропорциональна массе притягиваемо к земле тела:  . В общем виде ускорение свободного падения зависит от широты местности, и высоты подъема тела от нулевой отметки у поверхности Земли (высоты над уровнем моря). Если считать Землю шарообразным покоящимся телом с радиусом 6400 км, то ускорение свободного падения изменяется от поверхности Земли до высоты 20 км от 9,80 м/с2 до 9,75 м/с2.
. В общем виде ускорение свободного падения зависит от широты местности, и высоты подъема тела от нулевой отметки у поверхности Земли (высоты над уровнем моря). Если считать Землю шарообразным покоящимся телом с радиусом 6400 км, то ускорение свободного падения изменяется от поверхности Земли до высоты 20 км от 9,80 м/с2 до 9,75 м/с2. ,
,
 – радиус Земли.
– радиус Земли. .
.
 .
.
 системы, состоящей из поступательно движущегося тела переменной массы и отделяющегося за это время (или присоединяющихся) к нему частиц:
системы, состоящей из поступательно движущегося тела переменной массы и отделяющегося за это время (или присоединяющихся) к нему частиц: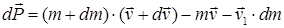 .
.
 – масса и скорость тела в момент времени t; dm и
– масса и скорость тела в момент времени t; dm и  – их изменения за малый промежуток dt;
– их изменения за малый промежуток dt;  – скорость отделяющихся частиц после отделения или присоединяющихся частиц до присоединения (их общая масса dm >0). После раскрытия скобок, приведения подобных слагаемых и исключения члена
– скорость отделяющихся частиц после отделения или присоединяющихся частиц до присоединения (их общая масса dm >0). После раскрытия скобок, приведения подобных слагаемых и исключения члена 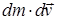 , ввиду его малости по сравнению с остальными, получаем:
, ввиду его малости по сравнению с остальными, получаем: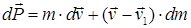 ,
,
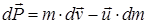 ,
,
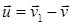 – скорость отделяющихся частиц после отделения (или присоединяющихся частиц до присоединения) относительно тела переменной массы. Подстановка (33) в закон изменения импульса (15) дает уравнение Мещерского:
– скорость отделяющихся частиц после отделения (или присоединяющихся частиц до присоединения) относительно тела переменной массы. Подстановка (33) в закон изменения импульса (15) дает уравнение Мещерского: .
.

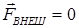 , получил уравнение движения ракеты:
, получил уравнение движения ракеты: ,
,
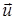 – скорость истечения продуктов сгорания топлива из сопла ракеты, измеренная относительно ракеты. Если начальная скорость ракеты равна нулю, а траектория движения прямая линия, то можно, решив уравнение (36), расчитать стартовую массу ракеты для достижения заданной скорости:
– скорость истечения продуктов сгорания топлива из сопла ракеты, измеренная относительно ракеты. Если начальная скорость ракеты равна нулю, а траектория движения прямая линия, то можно, решив уравнение (36), расчитать стартовую массу ракеты для достижения заданной скорости: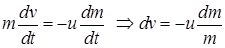
 .
.



