Движение материальной точки по окружности

 

При движении материальной точки по окружности (см. рис.2) можно описывать движение аналогично поступательному движению в декартовых координатах. Но поскольку окружность – кривая центрально симметричная, образованная вращением постоянного радиуса-вектора относительно его начала, то удобнее пользоваться полярными координатами с оговоркой того, что траектория движения – окружность радиуса R.

y

2 ,

1

x

 

Рис. 2. Пример плоского вращательного движения.

Тогда, для описания движения достаточно фиксировать закон изменения угла поворота со временем . Углы поворота измеряются в радианах ([φ] – рад). Понятно, что угол поворота величина векторная. Положительные направления угла поворота принято считать в направлении поворота от оси x к оси у как показано на рис.3.

Аналогично поступательному движению определяется угловая скорость, как первая производная угла поворота по времени:

(3)

Направление вектора угловой скорости выбирается по следующим правилам:

1. Вектор угловой скорости лежит на оси вращения z;

2. Направления вектора выбираем туда, куда закручивается правый винт по направлению движения тела (см. рис.3).

В дальнейшем ось вращения всегда будет определяться как ось z.

Если в результате исследования обнаруживается, что угловая скорость остается постоянной (), то движение тела по окружности называется равномерным.

 

z

 

 

O y

 

 

x

 

Рис. 3. Пояснение к выбору направления угловых скоростей и ускорений.

 

Для равномерного движения по окружности вводят понятия периода обращения тела по окружности и частоты (линейной) вращения. Периодом обращения тела по окружности (T) называют время одного полного оборота. Частотой вращения называют число оборотов за одну секунду, или величину обратную периоду:

(4)

Размерность периода обращения секунда ([ T ] – c), а частоты – обратная секунда или Герц ([ f ] – c^-1=Гц). Угловую скорость движения тела по окружности, только при равномерном движении, называют циклической частотой вращения тела. Связь между линейной частотой и циклической следующая: .

Аналогично поступательному движению определяют угловое ускорение, как первая производная угловой скорости по времени, или вторая производная от угла поворота по времени:

 

.

(5)

Направление вектора углового ускорения определяется аналогично направлению угловой скорости (см. рис.3). Если тело разгоняется, то угловое ускорение совпадает с угловой скоростью, а если тело тормозиться, то угловое ускорение направлено против угловой скорости (см. рис.3).

Получим соотношения между линейными скоростями и ускорениями и угловыми. Линейная скорость связана с угловой соотношением:

.

(6)

Его не трудно получить из определения скорости:

(7)

Для вывода формулы (7) достаточно рассмотреть малое перемещение dS от точки 1 к точке 2 (см. рис.2),которое видно из начала координат под углом d φ. Треугольник, образованный векторами прямоугольный, так как вектор перемещения , образующий хорду окружности бесконечно мал. Поэтому , как известно , поэтому .

Для вывода формулы линейного ускорения продифференцируем формулу (6):

.

(8)

Получили, что полное ускорение определяется суммой двух векторов и . Рассмотрим, куда направлены эти вектора. Вектор направлен туда же куда и линейная скорость, по касательной к окружности, его называют тангенциальным ускорением и обозначают . Тангенциальным по тому, что направлен по касательной к окружности, то есть туда же куда и скорость. Второй вектор направлен к центру окружности, его называют нормальным, радиальным или центростремительным ускорением, и обозначают . По модулю нормальное и тангенциальное ускорения равны произведению соответствующих скаляров векторов, входящих в векторные произведения:

.

(9)

 

Динамика. Энергия и импульс

 

Пока для описания движения определяли только величины, такие как перемещение, скорость и ускорение. Если тело движется с ускорением, то постулируется, что на тело действует сила, обеспечивающая разгон или торможение. Сила, векторная величина, определяемая как:

,

(10)

где m – масса тела. Размерность силы – Ньютон ([ F ] – кг·м/с²=Н). Сила, радиус-вектор, скорость и ускорение являются фундаментальными физическими величинами, определяющими характер движения. Масса тела, определяется как коэффициент пропорциональности между силой и ускорением. Для того, чтобы измерить массу тела необходимо два тела, эталонное и измеряемое, привести в движение с одинаковой силой и сравнить их ускорения.

После определения силы, можно постулировать три закона механики (законы Ньютона).

1. Если на тело не действуют ни какие силы, или сумма всех сил, действующих на тело равна нулю (равнодействующая сила), то тело или покоится или движется равномерно.

2. Сила, действующая на тело, или равнодействующая сила, равна произведению массы тела на его ускорение.

3. Если два тела приведены во взаимодействие с постоянной силой, то сила, действующая на первое тело, равна по модулю и противоположна по направлению, силе противодействия второго тела на первое.

Законы Ньютона выполняются только в инерциальных системах координат. Инерциальными называют системы координат, которые ии покоятся или движутся с постоянной скоростью.

Если на тело действует сила, то помимо того, что тело приобретает ускорение под действием этой силы, – то сила совершает работу. Работа силы определяется как интеграл по пути действия силы:

.

(11)

На математическом жаргоне: работа силы – сила, размазанная по пути ее действия. Размерность работы силы – Джоуль ([ A ] – кг·м/с²·м=Н·м=Дж). Из определения работы силы (11), силу, действующую на тело, можно определить как скорость нарастания работы силы по расстоянию. Очевидно, что если сила постоянна, то работа силы A=F·l, где l – расстояние, на котором сила действовала.

Силы, действующие на тело, классифицируются по трем признакам: по природе действия, виду и работе силы.

По природе действия силы разделяются на внешние и внутренние. По виду силы разделяют на:

1. Силы прямого действия.

2. Силы сопротивления (трения).

3. Силу тяжести.

4. Силу Кулона (электростатического взаимодействия).

5. Силу магнитного взаимодействия.

6. Ядерные силы.

По характеру работы, совершаемой силой, силы делят на консервативные и диссипативные. Консервативными называют силы, работа которых не зависит от пути действия. Диссипативными называют силы, работа которых зависит от пути.

Если тело движется с некоторой скоростью, то говорят, что оно обладает кинетической энергией. Кинетической энергией тела называют величину:

.

(12)

Кинетическая энергия определяет работу, которую может совершить тело с массой m и обладающее скоростью v. Кроме кинетической энергии в механике определяют потенциальную энергию тела (U). Потенциальной энергией, называют энергию, которой тело может обладать и при предоставлении телу свободы эта энергия перейдет в кинетическую. Связь между потенциальной энергией и силой, действующей на тело, готовой совершить работу:

.

(13)

Размерность энергии – Джоуль.

Прямым следствием первого закона Ньютона является определение импульса тела. Импульсом или количеством движения, называется векторная величина:

.

(14)

Размерность импульса – [P] – кг·м/с. Определим физический смысл импульса:

.

(15)

Следовательно, скорость нарастания импульса – сила, действующая на тело. Поэтому импульс называют также количеством движения тела: при одинаковой тормозной силе действующей на два тела, время движения тел до остановки пропорционально их импульсам.

Моментом силы и моментом импульса называют векторные величины:

.

(16)

Можно доказать соотношение между векторами и :

.

(17)

Векторное произведение , т.к. вектора скорости и импульса колинеарны.

Первый закон Ньютона не дает однозначного ответа на вопрос о равновесии системы тел. Из него только лишь следует достаточное условия равновесия – сумма всех сил, действующих на тело равна нулю. Необходимым условием равновесия является равенство нулю суммы моментов всех сил, приложенных к телу.

Из условия равновесия тел можно определить точку в теле, относительно которую сумма всех моментов сил других точек будет равна нулю. Эта точка называется центром масс тела. Положение центра масс тела определяется соотношением:

,

(18)

где ρ – плотность тела; начало координат ставится на центр масс, и интеграл берется по всему объему тела. Для описания движения в рамках модели материальной точки необходимым условием решения основной задачи механики является построение зависимости в котоой координатами радиус-вектора будут координаты центра масс тела. Величину 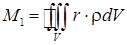, вычисленную относительно начала координат называют механическим моментом тела первого порядка.