
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Номера заданий контрольной работы № 1 по подгруппамСтр 1 из 9Следующая ⇒
1 курс (группа 9652) заочная форма обучения 21.03.01 «Нефтегазовое дело», Профиль «Эксплуатация и обслуживание технологических объектов нефтегазового производства» Группа 1 Подгруппа 1
Группа 1 Подгруппа 2
Группа 2 Подгруппа 1
Группа 2 Подгруппа 2
Группа 3 Подгруппа 1
Группа 3 Подгруппа 2
Группа 4 Подгруппа 1
Группа 4 Подгруппа 2
Механика
Глава 1. Кинематика материальной точки Контрольные вопросы 1. Что изучает физика? 2. Как строится система единиц? Назовите основные и дополнительные физические величины СИ и единицы их измерения. 3. Назовите дольные и кратные приставки в СИ от 10-12 до 1012. 4. Какими свойствами обладают пространство и время в механике Ньютона? 5. Перечислите основные понятия кинематики и поясните их. 6. Что означает задать движение? Какие способы задания движения Вы знаете? Поясните их суть. 7. Что такое скорость и ускорение? Как найти величину скорости и ускорения? 8. Какие движения означают равенства: v = const и 9. Что Вы можете сказать о движениях при которых a = const и 10. Охарактеризуйте ускорение при криволинейном движении. Начертите треугольник ускорений для a т < 0. 11. Вспомните определения угловых характеристик движения и направления векторов 12. Установите связи между линейными и угловыми характеристиками движения. 13. Запишите законы перемещения и скорости в векторной форме и в проекциях на оси координат. 14. Установите связь между формулами пути и скорости, с одной стороны, и углового перемещения и угловой скорости – с другой. Основные формулы Скорость где
ускорение
При равнопеременном движении (
где Формулы (*) и (**) дают возможность графически решать задачи на нахождение Основным методом решения задач в физике является аналитический (численный) метод. Для этого уравнения (*) и (**) проектируют на выбранные оси координат (оси движений), после чего решают полученные скалярные уравнения. В проекциях эти уравнения выглядят так
(аналогично на оси 0Y и 0Z).
Если движение происходит в одном направлении, то (***) дает пройденный путь
В случае равномерного (а = 0) движения
Средняя скорость
В случае равнопеременного движения в одном направлении
где
Скорость сложного движения
где
Аналогично для ускорений
При криволинейном движении полное ускорение
где Модуль полного ускорения
где R - радиус кривизны траектории в данной точке.
При вращении твердого тела около неподвижной оси (или движения точки по окружности) угловая скорость
угловое ускорение
При равнопеременном вращении (
(знак “ - “ у e соответствует равнозамедленному вращению).
Связь линейных и угловых характеристик движения:
Если
где Т - период вращения; n - число оборотов в с; n - частота вращения.
Полезно помнить следующие два соотношения для равнопеременных движений
Методические указания Наиболее распространенными в нашем случае являются задачи, когда материальная точка движется в плоскости с постоянным ускорением. Для их решения рекомендуется придерживаться следующего порядка: 1. Выбрать прямоугольную систему координат с осями ОХ и ОУ лежащими в плоскости, в которой движется материальная точка, и начертить в ней предполагаемую траекторию движения. 2. Спроектировать векторные уравнения движения (*) и(**) на выбранные оси и записать их в форме (***). Теперь решение задачи сведется к решению полученной системы уравнений. 3. Выбор осей определяется условием конкретной задачи. При этом надо стремиться, чтобы часть проекций векторов оказалась равной нулю. Начало координат чаще всего совмещается с положением точки в начальный момент времени.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.145.114 (0.13 с.) |
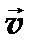 = const?
= const? = const?
= const? ,
, 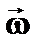 ,
,  .
. ,
, - радиус вектор точки;
- радиус вектор точки;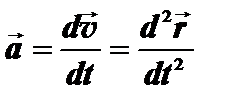 .
. ) скорость и перемещение выражаются соотношениями
) скорость и перемещение выражаются соотношениями (*),
(*),  (**),
(**), - начальная скорость.
- начальная скорость. .
. ,
,  (***)
(***) .
. .
. .
. ,
,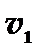 ,
,  - скорости точки в моменты времени
- скорости точки в моменты времени  и
и  .
.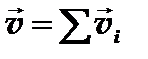 ,
, - скорости простых движений.
- скорости простых движений. .
. ,
, - нормальное ускорение,
- нормальное ускорение,  - тангенциальное (касательное) ускорение.
- тангенциальное (касательное) ускорение. ,
, ,
,  ,
, ,
, .
. )
)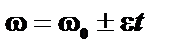 ,
, .
.

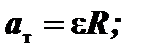

 .
.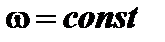 (равномерное вращение), то
(равномерное вращение), то 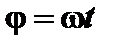 ;
; ,
, ;
;  .
.


