
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи для контрольной работы ⇐ ПредыдущаяСтр 4 из 4
Даны функция а) градиент данной функции в точке М; б) производную этой функции в точке 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
2.5.Экстремумы функций двух переменных. Наибольшее и наименьшее значения. 2.5.1. Экстремумы функций двух переменных. Говорят, что функция а) найти б) найти точки, в которых одновременно в) вычислив в каждой найденной критической точке (
выяснить знак выражения Если Если Пример. Исследовать на экстремум функцию Решение. Имеем элементарную функцию, определенную при любых действительных значениях переменных а) Найдем частные производные б) Найдем критические точки (точки, подозрительные на экстремум), из системы уравнений
или
Из первого уравнения системы
Второе уравнение системы преобразуется к виду
Подставляя найденные значения поочерёдно в первое уравнение системы, получим Таким образом, заданная функция имеет две критические точки в) Найдем вторые частные производные данной функции:
Имеем в точке Значит Далее, в точке Следовательно,
Ответ: 2.5.2. Наибольшее и наименьшее значения функции в замкнутой ограниченной области D. Всякая непрерывная функция
а) Найти частные производные
при этом рассмотреть лишь те из них, которые расположены внутри области D. б) Вычислить значения данной функции в) Определить наибольшее и наименьшее значения функции на каждом участке границы области D. При этом, выражая переменную у или переменную х из уравнения соответствующего участка границы, будем всякий раз иметь функцию одной переменной на некотором отрезке. Исследование такой функции на наибольшее и наименьшее значение – знакомая задача (см. п. 1.5.1). г) Среди значений, найденных в п. б) и в) выбрать наибольшее и наименьшее. Пример. Найти наименьшее и наибольшее значения функции
а) Найдем частные производные данной функции
Преобразуем систему к виду
Откуда Итак, данная функция имеет единственную стационарную точку
б) Исследуем поведение функции на границе области На участке границы Итак, нахождению подлежит значение функции в точке На участке границы Из уравнения прямой (участка границы)
Далее, В точке
Остается вычислить значения данной функции в концевых точках участков границы (в угловых точках области
Сравнивая эти значения, находим, что наибольшее из них равно 6 и достигается в точках Ответ:
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.96 (0.124 с.) |
 и точка М. Найти:
и точка М. Найти: по направлению вектора
по направлению вектора 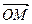 , где точка
, где точка  - начало координат.
- начало координат. . 14.
. 14. 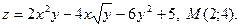
 . 15.
. 15. 
 . 16.
. 16. 
 . 17.
. 17. 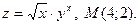
 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
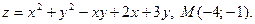 23.
23. 
 24.
24. 
 25.
25. 
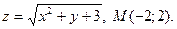
 достигает максимума (минимума) в точке
достигает максимума (минимума) в точке 
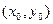 , если ее значение
, если ее значение  в указанной точке является наибольшим (наименьшим) по сравнению со значениями
в указанной точке является наибольшим (наименьшим) по сравнению со значениями  из некоторой окрестности точки
из некоторой окрестности точки  и обладает в
и обладает в 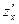 и
и 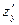 ;
; и
и  (критические точки);
(критические точки); ) частные производные второго порядка
) частные производные второго порядка ,
, .
. , то в данной критической точке (
, то в данной критической точке ( имеется минимум, в случае
имеется минимум, в случае  - максимум.
- максимум. , то в данной критической точке экстремума нет.
, то в данной критической точке экстремума нет. .
. и
и 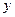 . В соответствии с изложенным алгоритмом
. В соответствии с изложенным алгоритмом ,
,  .
. , которая в нашем случае имеет вид
, которая в нашем случае имеет вид 

 , следовательно
, следовательно
 , откуда
, откуда  ,
,  .
. ,
, 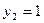 .
.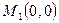 и
и 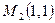 .
.
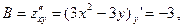


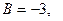

 в точке
в точке 

 , то в точке
, то в точке 
 .
. достигает в такой области D своего наибольшего и наименьшего значения. В частности, для элементарных функций может быть использован следующий алгоритм нахождения этих значений.
достигает в такой области D своего наибольшего и наименьшего значения. В частности, для элементарных функций может быть использован следующий алгоритм нахождения этих значений. в замкнутой области D, ограниченной линиями
в замкнутой области D, ограниченной линиями 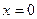 ,
,  ,
,  .
. Решение. Данная элементарная функция определена при любых действительных значениях переменных
Решение. Данная элементарная функция определена при любых действительных значениях переменных  , ограниченная указанными линиями, изображена на рисунке
, ограниченная указанными линиями, изображена на рисунке  .
. ,
,  и определим критические точки:
и определим критические точки:
 или
или  ,
, и, следовательно,
и, следовательно,  .
. , которая, очевидно, принадлежит области
, которая, очевидно, принадлежит области 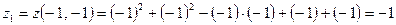 .
. ,
,  . Тогда
. Тогда  и
и 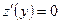 , если
, если  , откуда
, откуда  .
. , принадлежащей границе области
, принадлежащей границе области 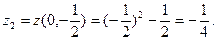
 ,
,  . Тогда
. Тогда  и
и  при
при  . В точке
. В точке  , принадлежащей границе области
, принадлежащей границе области 

 или
или  ,
,  и
и  , откуда
, откуда  . Тогда
. Тогда 
 , принадлежащей границе области
, принадлежащей границе области 

 ,
, ,
, .
. ,
,  , а наименьшее значение равно -1 и достигается в точке
, а наименьшее значение равно -1 и достигается в точке  достигается в точках
достигается в точках  достигается в точке
достигается в точке 


